Giải bài tập Hình học 9, chương I: Bài 2: Tỉ số lượng giác của góc nhọn
2019-08-02T00:24:34-04:00
2019-08-02T00:24:34-04:00
Giải bài tập Hình học 9, chương I: Bài 2: Tỉ số lượng giác của góc nhọn
/themes/cafe/images/no_image.gif
Bài Kiểm Tra
https://baikiemtra.com/uploads/bai-kiem-tra-logo.png
Thứ sáu - 02/08/2019 00:20
Giải bài tập Hình học 9, chương I: Bài 2: Tỉ số lượng giác của góc nhọn
Bài 1. Vẽ một tam giác vuông. Có một góc nhọn 34o rồi viết các tỉ số lượng giác của góc 34o là:
Giải:
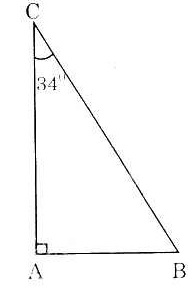
Giả sử ta vẽ tam giác ABC vuông tại A, có góc 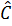 = 34o . = 34o .
Khi đó, các tỉ số lượng giác của góc 34o là:
sin34° = sinC = 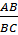 cos 34o = cos C = cos 34o = cos C = 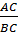
tg34o = tgC = 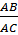 cotg34o = cotg34o = cotgC = cotg34o = cotg34o = cotgC = 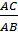 |
 |
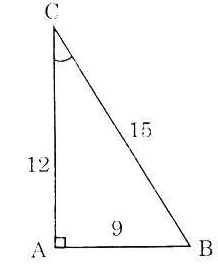
Bài 2. Cho tam giác ABC vuông tại C, trong đó AC = 0,9m, BC = 1,2m. Tính các tỉ số lượng giác của góc B. Từ đó suy ra các tỉ số lượng giác của góc A.
Giải:
Áp dụng định lý Pytago trong tam giác vuông ABC, ta có:
AB2 = CA2 + CB2 = 92 + 122
AB2 = 225
⇒ AB = 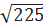 = 15 (m) = 15 (m)
Vậy: sinB = 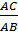 = = 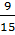 = = 
cosB = 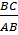 = = 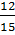 = = 
tgB = 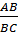 = = 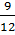 = = 
cotgB = 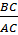 = = 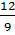 = = 
* Vì 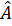 và và 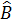 là hai góc phụ nhau (do là hai góc phụ nhau (do  ABC vuông tại C) ABC vuông tại C)
sinA = cosB =  ; sinB = cosA = ; sinB = cosA = 
tgA = cotgB =  ; tgB = cotgA = ; tgB = cotgA =  |
 |
Bài 3. Hãy viết các tỉ số lượng giác sau thành tỉ số lượng giác của các góc nhỏ hơn 45°:
sin 60°, cos75°, sin52°30’, cotg82°, tg80°.
Giải:
Vì góc 60° và góc 30° là hai góc phụ nhau, nên: sin 60° = cos 30°
- Tương tự, 75o và 15° lá hai góc phụ nhau, nên: cos75° = sin15°
- Góc 52°30’ và góc 37o30’là hai góc phụ nhau, nên: sin52°30’ = cos37o30’
- Góc 82° và góc 8o là hai góc phụ nhau, nên: Cotg82° = tg8o
- Góc 80° và góc 10° là hai góc phụ nhau, nên: tg80° = cotg10o
BÀI TẬP LÀM THÊM
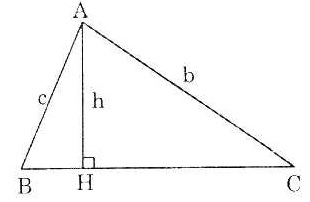
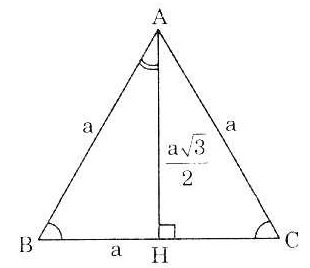
Bài 1. Cho tam giác đều ABC cạnh a, đường cao AH. Tính các tỉ số lượng giác của các góc 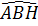 và
và 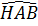 .
Giải:
.
Giải:
* 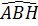 = 60° (góc A đều) = 60° (góc A đều)
* 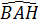 = 30° (AH cũng là phân giác) = 30° (AH cũng là phân giác)
* AB = AC = BC = a ( ABC đều) ABC đều)
*Vận dụng định nghĩa về các tỉ số lượng giác sẽ tính được: |
 |
sin 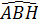 = sin 60o =
= sin 60o = 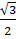 ; cos
; cos 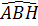 = cos 60o =
= cos 60o =  tg
tg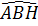 = tg60o =
= tg60o = 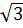 ; cotg
; cotg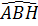 = cotg60o =
= cotg60o = 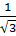 =
= 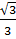 sin
sin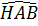 = sin30o =
= sin30o =  ; cos
; cos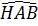 = cos30o =
= cos30o = 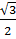 tg
tg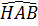 = tg30o =
= tg30o = 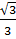 ; cotg
; cotg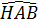 = cotg30o =
= cotg30o = 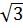
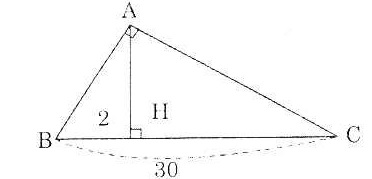
| Bài 2. Cho tam giác ABC vuông ở A, kẻ đường cao AH. Cho BC = 30cm, BH = 2cm, chứng minh tgB = 14tgC. |
 |
Giải:
Ta có: HC = BO - BH = 30 - 2 = 28 (cm)
 ABH vuông tại H nên: tgB =
ABH vuông tại H nên: tgB = 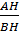 =
= 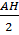 (1)
(1)
 ACH vuông tại H nên: tgC =
ACH vuông tại H nên: tgC = 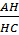 =
= 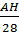 (2)
Từ (1) và (2) ta suy ra:
(2)
Từ (1) và (2) ta suy ra: 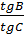 =
= 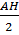 :
: 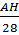 =
= 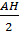 .
. 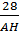 Vậy tgB = 14tgC
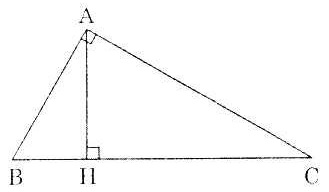
Bài 3. a) Cho tam giác ABC có 3 góc nhọn.
Chứng minh rằng:
Vậy tgB = 14tgC
Bài 3. a) Cho tam giác ABC có 3 góc nhọn.
Chứng minh rằng: 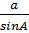 =
= 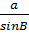 =
= 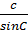 b)
b)  ABC có
ABC có 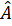 nhọn
Chứng minh rằng
nhọn
Chứng minh rằng 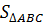 =
=  b.c.sinA
c)
b.c.sinA
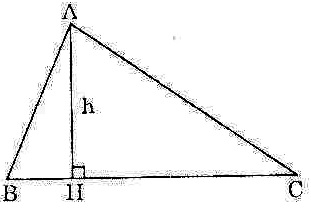
c)  ABC có 3 góc nhọn , đường cao AH = h, cạnh BC = a. Chứng minh rằng cotgB + cotgC = 2 khi và chỉ khi a = 2h.
Giải:
ABC có 3 góc nhọn , đường cao AH = h, cạnh BC = a. Chứng minh rằng cotgB + cotgC = 2 khi và chỉ khi a = 2h.
Giải:
a) Dựng đường cao AH, ta có:
sinB = 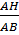 ; sinC = ; sinC = 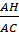
⇒ 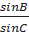 = = 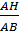 . . 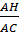 |
|
⇒ 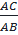 =
=  ⇒
⇒ 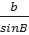 =
= 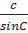 Tương tự:
Tương tự: 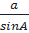 =
= 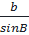 Từ đó ta có:
Từ đó ta có: 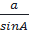 .
. 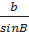 =
= 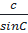
b) Kẻ CH vuông góc với AB, ta có: CH = AC. sin A
⇒ 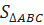 = =  = =  (AB.AC.sinA) (AB.AC.sinA)
Tức là: 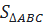 = =  b.c.sinA b.c.sinA
c) Giả sử:
cotgB + cotgC = 2
Ta có:
cotgB = 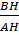 , cotgC = , cotgC = 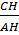
⇒ cotgB + cotgC = 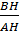 + + 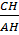 = = 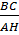
( ABC nhọn nên H thuộc BC) ABC nhọn nên H thuộc BC)
Như vậy: 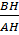 = 2 ⇒ a = 2h = 2 ⇒ a = 2h
Ngược lại, giả sử: a = 2h
Ta có: cotgB = 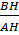 , cotgC = , cotgC = 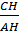
⇒ cotgB + cotgC = 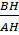 + + 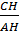 = = 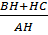
= 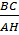 = =  = = 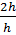 = 2 = 2 |
|
| Bài 4. Một tam giác vuông có một góc 60o và cạnh huyền là 8. Hãy tìm độ dài của cạnh đối diện với góc 60o. |
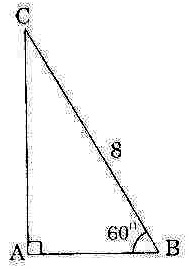 |
Giải:
Giả sử:  ABC vuông tại A, có
ABC vuông tại A, có 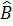 = 60o ; BC = 8. Tính độ dài AC.
Từ tam giác vuông ABC, ta có: sinB – sin60o =
= 60o ; BC = 8. Tính độ dài AC.
Từ tam giác vuông ABC, ta có: sinB – sin60o = 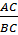 ⇒ AC – sin60o. BC
Mà: sin60o =
⇒ AC – sin60o. BC
Mà: sin60o = 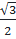 ; BC = 8 ⇒ AC =
; BC = 8 ⇒ AC = 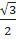 .8 = 4
.8 = 4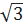 Vậy cạnh đối diện với góc 60o là 4
Vậy cạnh đối diện với góc 60o là 4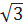 Bài 5. Chứng tỏ rằng: cos2x + cos2y =
Bài 5. Chứng tỏ rằng: cos2x + cos2y = 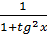 +
+ 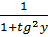 Giải:
Trước hết ta chứng minh: cos2x =
Giải:
Trước hết ta chứng minh: cos2x = 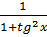 Biết rằng: 1 = cos2x + sin2 x ⇒ (1)
Biết rằng: 1 = cos2x + sin2 x ⇒ (1) 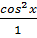 =
= 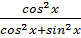 (1)
Ta cũng có: tgx =
(1)
Ta cũng có: tgx = 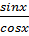 ⇒ sinx = cosx.tgx ⇒ sin2x = cos2x.tg2x
Từ (1) ⇒ cos2x =
⇒ sinx = cosx.tgx ⇒ sin2x = cos2x.tg2x
Từ (1) ⇒ cos2x = 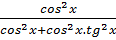 (2)
Đơn giản cos2x ở tử và mẫu của vế phải ở (2): cos2x =
(2)
Đơn giản cos2x ở tử và mẫu của vế phải ở (2): cos2x = 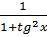 Chứng minh tương tự, ta có: cos2y =
Chứng minh tương tự, ta có: cos2y = 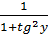 Vậy: cos2x + cos2y =
Vậy: cos2x + cos2y = 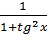 +
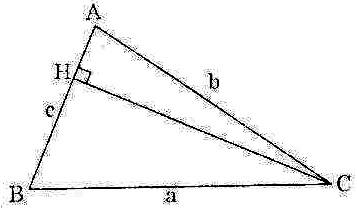
+ 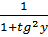 Bài 6. Cho tam giác ABC vuông tại A, đường cao AH. Biết tỉ số lượng giác của các góc nhọn trong
Bài 6. Cho tam giác ABC vuông tại A, đường cao AH. Biết tỉ số lượng giác của các góc nhọn trong  ABC, hãy chứng minh:
ABC, hãy chứng minh: 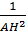 =
= 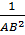 +
+ 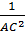 Giải:
Giải:
Từ tam giác vuông AHB, ta suy ra:
sinB = 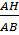
⇒ sin2B = 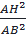 (1) (1) |
|
Từ tam giác vuông AHC, suy ra:
sinC = 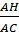 = cosB (do
= cosB (do 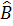 +
+ 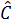 = 90o) ⇒ cos2B =
= 90o) ⇒ cos2B = 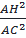 (2)
Cộng (1) và (2) theo vế:
sin2B + cos2B =
(2)
Cộng (1) và (2) theo vế:
sin2B + cos2B = 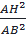 +
+ 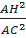 1= AH2
1= AH2 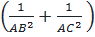 (do sin2B + cos2B = 1)
⇒
(do sin2B + cos2B = 1)
⇒ 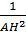 =
= 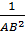 +
+ 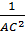 (đpcm)
(đpcm)
© Bản quyền thuộc về
Bài kiểm tra. Ghi rõ nguồn Bài kiểm tra.com khi sao chép nội dung này.