Giải bài tập Hình học 9, chương II: Bài 6: Tính chất của hai tiếp tuyến cắt nhau
2019-08-06T00:25:22-04:00
2019-08-06T00:25:22-04:00
Giải bài tập Hình học 9, chương II: Bài 6: Tính chất của hai tiếp tuyến cắt nhau
/themes/cafe/images/no_image.gif
Bài Kiểm Tra
https://baikiemtra.com/uploads/bai-kiem-tra-logo.png
Thứ ba - 06/08/2019 00:22
Giải bài tập Hình học 9, chương II: Bài 6: Tính chất của hai tiếp tuyến cắt nhau
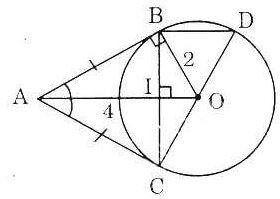
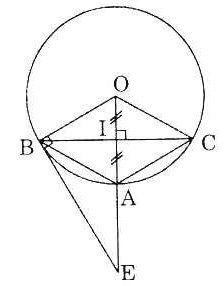
Bài 1. Cho đường tròn (O), điểm A nằm bên ngoài đường tròn. Kẻ các tiếp tuyến AB, AC với đường tròn (B, C là các tiếp điểm).
a) OA vuông góc với BC.
b) Vẽ đường kính CD. Chứng minh rằng BI) song song với AO.
c) Tính độ dài các cạnh của tam giác ABC biết OB = 2cm, OA = 4cm.
Giải:
a) Vì AB và AC là hai tiếp tuyến của (O) nên AB = AC.
Suy ra  ABC cân tại A.
Ta còn có AO là đường phân giác của
ABC cân tại A.
Ta còn có AO là đường phân giác của 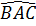 của tam giác cân ABC nên AO cùng là đường cao.
Vậy AO ⊥ BC
của tam giác cân ABC nên AO cùng là đường cao.
Vậy AO ⊥ BC
b) Gọi I là giao điểm của AO với BC.
Ta có  IBA = IBA =  ICA (ch-gn) ICA (ch-gn)
⇒ IB = IC
Trong tam giác BCD ta có:
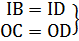 ⇒ OI là đường trung bình của ABCD ⇒ OI là đường trung bình của ABCD
nên OI // BD hay AO // BD
Vậy AO // BD (đpcm) |
|
c) Vì AB là tiếp tuyến của (O) với B là tiếp điếm nên AB ⊥ OB và AB = AC.
Vậy  OAB vuông tại B.
Áp dụng định lý Pytago trong tam giác vuông OAB, ta có:
AO2 = AB2 + BO2
⇒ AB2 = AO2 – BO2 = 42 – 22 = 12
⇒ AB =
OAB vuông tại B.
Áp dụng định lý Pytago trong tam giác vuông OAB, ta có:
AO2 = AB2 + BO2
⇒ AB2 = AO2 – BO2 = 42 – 22 = 12
⇒ AB = 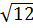 = 2
= 2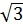 (cm)
- Trong tam giác vuông OAB ta có:
sinOAB =
(cm)
- Trong tam giác vuông OAB ta có:
sinOAB = 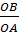 =
=  =
=  ⇒
⇒ 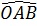 = 30° ⇒
= 30° ⇒ 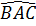 = 2
= 2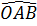 = 2.30o = 60o
- Tam giác ABC cân tại A và có
= 2.30o = 60o
- Tam giác ABC cân tại A và có 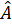 = 60o nên
= 60o nên  ABC là tam giác đều.
Suy ra AB = BC = CA = 2
ABC là tam giác đều.
Suy ra AB = BC = CA = 2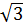 (cm)
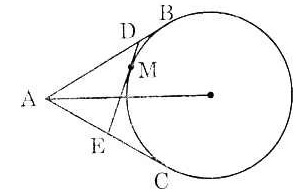
Bài 2. Từ một điếm A nằm bên ngoài đường tròn (O), kẻ tiếp tuyến AB, AC với đường tròn (B, C là các tiếp điểm). Qua điểm M thuộc cung nhỏ BC, kẻ tiếp tuyến thứ ba với đường tròn (O), nó cắt các tiếp tuyến AB và AC theo thứ tự ở D và K. Chứng minh rằng chu vi tam giác ADE bằng 2AB.
Giải:
(cm)
Bài 2. Từ một điếm A nằm bên ngoài đường tròn (O), kẻ tiếp tuyến AB, AC với đường tròn (B, C là các tiếp điểm). Qua điểm M thuộc cung nhỏ BC, kẻ tiếp tuyến thứ ba với đường tròn (O), nó cắt các tiếp tuyến AB và AC theo thứ tự ở D và K. Chứng minh rằng chu vi tam giác ADE bằng 2AB.
Giải:
Ta có:
AB = AC;
DB = DM;
EC = EM.
Chu vi  ADE: ADE:
AD + AE + DE = AD + DM + AE + EM
= AD + DB + AE + EC = AB + AC = 2AB. |
|
Bài 3. Cho góc xAy khác góc bẹt. Tâm của các đường tròn tiếp xúc với hai cạnh của góc xAy nằm trên đường nào?
Giải: Các đường tròn tiếp xúc với hai cạnh của một góc thì có tâm cách đều hai cạnh của góc đó. Vậy tâm của chúng nằm trên tia phân giác At của góc xAy.
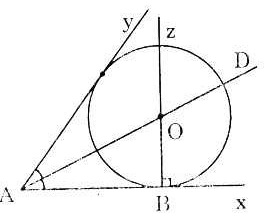
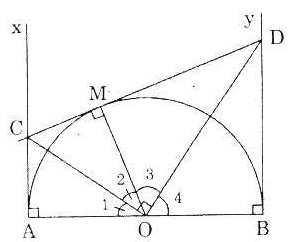
Bài 4. Cho góc xAy khác góc bẹt, điểm B thuộc tia Ax. Hãy dựng đường tròn (O) tiếp xúc với Ax tại B và tiếp xúc với Ay.
Giải:
Cách dựng:
- Dựng tia phân giác At của góc xAy.
- Dựng đường thẳng Bz qua B và vuông góc với tia Ax.
- Giao điểm O của At và Bz là tâm của đường tròn cần dựng.
- Dựng đường tròn tâm O, bán kính R = OB, ta được đường tròn cần dựng. |
|
BÀI TẬP LÀM THÊM
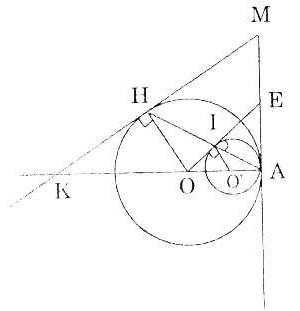
Bài 1. Cho đường tròn (O; 8) và O’; 3) tiếp xúc trong tại A. Đường thẳng qua (O) và tiếp xúc với (O’) tại I cắt tiếp tuyến chung (tiếp điểm là A) tại E.
a) Tính độ dài các đoạn thẳng OI và AE. Tia AI cắt (O) tại H. Tiếp tuyến của (O) tại H cắt tia AO tại K và cắt AE tại M.
b) Chứng minh KM // OE và O’I // OH
c) Tính AM và bán kính đường tròn ngoại tiếp tam giác AMH. |
 |
Giải:
a) OI tiếp xúc với (O’):
⇒ 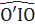 = 90o
⇒ OI2 = OO’2 - O’I2 = 52 – 32 = 42 ⇒ OI = 4 (cm)
= 90o
⇒ OI2 = OO’2 - O’I2 = 52 – 32 = 42 ⇒ OI = 4 (cm)
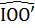 =
= 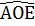 ,
, 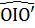 =
= 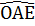 =
= 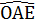 ⇒
⇒  OIO’
OIO’ 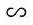
 OAE ⇒
OAE ⇒ 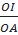 =
= 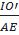 ⇒
⇒  =
= 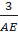 ⇒ AE = 6 (cm)
b) EI = EA ⇒ EIA = EAI (1)
MH = MA ⇒
⇒ AE = 6 (cm)
b) EI = EA ⇒ EIA = EAI (1)
MH = MA ⇒ 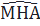 =
= 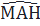 (2)
(2)
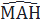 =
= 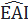 (3)
Từ (1), (2) và (3)
⇒
(3)
Từ (1), (2) và (3)
⇒ 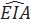 =
= 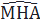 ⇒
⇒ 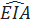 và
và 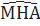 đồng vị ⇒ KM//OE
Mà OH ⊥ KM, O’I ⊥ OE ⇒ O’I //OH
c) O’I//OH ⇒
đồng vị ⇒ KM//OE
Mà OH ⊥ KM, O’I ⊥ OE ⇒ O’I //OH
c) O’I//OH ⇒  =
= 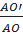 =
=  (1)
IE//HM ⇒
(1)
IE//HM ⇒ 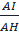 =
= 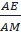 (2)
Từ (1) và (2): ⇒
(2)
Từ (1) và (2): ⇒ 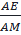 =
=  ⇒
⇒ 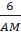 =
=  ⇒ AM = 16 (cm)
⇒ AM = 16 (cm)
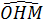 =
= 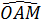 = 90o
⇒ A, H thuộc đường tròn đường kính OM
⇒ Đường tròn ngoại tiếp
= 90o
⇒ A, H thuộc đường tròn đường kính OM
⇒ Đường tròn ngoại tiếp  AMH có đường kính là OM
OM2 = OA2 + AM2 = 82 + 162 = 64 + 256 = 320
⇒ OM =
AMH có đường kính là OM
OM2 = OA2 + AM2 = 82 + 162 = 64 + 256 = 320
⇒ OM = 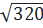 = 8
= 8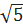 Vậy đường tròn ngoại tiếp
Vậy đường tròn ngoại tiếp  AMH có bán kính là 4
AMH có bán kính là 4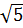 (cm).
(cm).
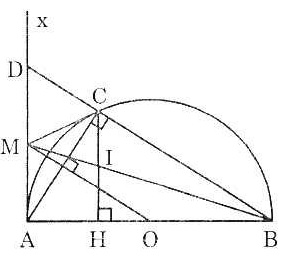
Bài 2. Cho nửa đường tròn đường kính AB. Trên nửa mặt phẳng chứa đường tròn ta dựng tia tiếp tuyến Ax. Từ điểm M trên Ax ta kẻ tiếp tuyến thứ hai MC với nửa đường tròn, kẻ CH ⊥ AB tại H; đường thẳng BC cắt Ax tại D. Chứng minh:
a) M là trung điểm AD
b) MB đi qua trung điểm của CH. |
 |
Giải:
a) Ta có: MA = MC (tính chất tiếp tuyến)
⇒ M thuộc trung trực AC
⇒ Mà OA = OC (bán kính)
⇒ O thuộc trung trực AC
Do đó MO là trung trực AC ⇒ MO ⊥ AC
Mặt khác 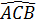 = 90°
(
= 90°
(  ACB vuông tại C vì CO = OA = BO =
ACB vuông tại C vì CO = OA = BO =  AB ) ⇒ AC ⊥ BD (2)
Từ (1) và (2) ⇒ MO // BD
Mà O là trung điểm AB ⇒ M là trung điểm AD.
b) Gọi I là giao điểm của CH và MB.
Ta có: CH // AD (cùng vuông góc với AB).
Áp dụng đinh lí Ta - lét ta có:
AB ) ⇒ AC ⊥ BD (2)
Từ (1) và (2) ⇒ MO // BD
Mà O là trung điểm AB ⇒ M là trung điểm AD.
b) Gọi I là giao điểm của CH và MB.
Ta có: CH // AD (cùng vuông góc với AB).
Áp dụng đinh lí Ta - lét ta có: 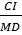 =
= 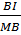 =
= 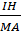 Mà MD = MA (chứng minh câu a) ⇒ CI = IH
Vậy MB đi qua trung điểm I của CH.
Mà MD = MA (chứng minh câu a) ⇒ CI = IH
Vậy MB đi qua trung điểm I của CH.
Bài 3. Cho đường tròn (O) và điểm M nằm bên ngoài đường tròn. Qua M vẽ hai tiếp tuyến MA, MB với đường tròn (O) trong đó A, B là các tiếp điểm sao cho AMB = 90o.
Qua điểm C trên cung nhỏ AB kẻ tiếp tuyến của đường tròn (O) cắt MA tại MB lần lượt ở P và Q. Chứng minh rằng:
 (MA + MB) < PQ < (MA + MB) < PQ <  (MA + MB) (MA + MB) |
|
Giải:
Theo tính chất hai tiếp tuyến của một đường tròn cắt nhau tại một điểm, ta có:
MA = MB, PA = PC và QB = QC
Do đó: PQ = PC + CQ
Hay PQ = PA + QB (1)
Tam giác MPQ vuông ở M, ta có:
PQ < PM + QM (2)
Từ (1) và (2), suy ra:
2PQ < (PA + PM) + (BQ + QM)
Hay: 2PQ = MA + AIB
Do đó: PQ <  (MA + MB)
Trong tam giác MPQ, ta lại có:
PQ > PM và PQ > QM
⇒ PQ > PM + MQ (3)
Từ (1) và (3), suy ra: PQ >
(MA + MB)
Trong tam giác MPQ, ta lại có:
PQ > PM và PQ > QM
⇒ PQ > PM + MQ (3)
Từ (1) và (3), suy ra: PQ >  (MA + MB)
Vậy
(MA + MB)
Vậy  (MA + MB) > PQ >
(MA + MB) > PQ >  (MA + MB)
Bài 4. Cho đường tròn (O) có bán kính OA = R, dây BC vuông góc với OA tại trung điểm của OA.
a) Tứ giác OCAB là hình gì? Vì sao?
b) Kẻ tiếp tuyến với đường tròn tại B, nó cắt đường thẳng OA tại E. Tính độ dài BE theo R là bán kính của (O).
Giải:
(MA + MB)
Bài 4. Cho đường tròn (O) có bán kính OA = R, dây BC vuông góc với OA tại trung điểm của OA.
a) Tứ giác OCAB là hình gì? Vì sao?
b) Kẻ tiếp tuyến với đường tròn tại B, nó cắt đường thẳng OA tại E. Tính độ dài BE theo R là bán kính của (O).
Giải:
a) Tứ giác OCAB là hình thoi. Thật vậy:
* Cách 1: Từ đề bài suy ra BC là trung trực của OA.
⇒ BO = BA và CO = CA mà BO = CO = bán kính
⇒ BO = BA = CO = CA
Vậy OCAB là hình thoi.
* Cách 2:
Ta có: OA ⊥ BC (gt)
⇒ IB = IC (I là giao điểm của OA và BC)
Ta cũng có IO = IA (gt)
⇒ OACB là hình thoi (vì có hai đường chéo vuông góc với nhau tại trung điểm của mỗi đường). |
|
b) Độ dài BE:
Ta có: BO = BA (B thuộc trung trực BC của OA)
⇒ BO = BA - AO - bán kính
⇒  OAB đều ⇒
OAB đều ⇒ 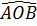 = 60o
⇒ Tam giác vuông OBE bằng nửa tam giác đều cạnh OE.
⇒ OE = 2OB = 2R
⇒ BE2 = OE2 – OB2 = 4R2 – R2 = 3R2
⇒ BE = R
= 60o
⇒ Tam giác vuông OBE bằng nửa tam giác đều cạnh OE.
⇒ OE = 2OB = 2R
⇒ BE2 = OE2 – OB2 = 4R2 – R2 = 3R2
⇒ BE = R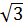
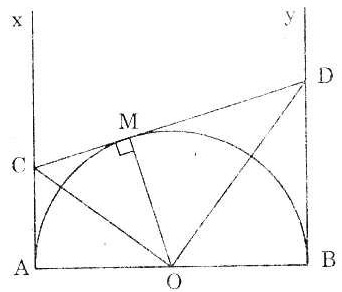
Bài 5. Cho nửa đường tròn tâm o đường kính AB. Gọi Ax, By là các tia vuông góc với AB (Ax và By nằm cùng phía với nứa đường tròn đối với đường thẳng AB). Qua một điểm M thuộc nửa đường tròn, kẻ tiếp tuyến với nửa đường tròn; tiếp tuyến cắt Ax tại C và cắt By tại D. Chứng minh rằng:
a) 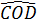 = 90o = 90o
b) CD = AC + BD
c) Tích AC.BD không đối khi điểm M di chuyển trên nửa đường tròn. |
|
Giải:
a) 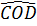 = 90o
Ta có:
Ax ⊥ AB tại A và By ⊥ AB tại B ⇒ Ax, By là hai tiếp tuyến của (O) và CD là tiếp tuyến có M là tiếp điểm (gt).
Theo tính chất của hai tiếp tuyến cắt nhau, ta có:
= 90o
Ta có:
Ax ⊥ AB tại A và By ⊥ AB tại B ⇒ Ax, By là hai tiếp tuyến của (O) và CD là tiếp tuyến có M là tiếp điểm (gt).
Theo tính chất của hai tiếp tuyến cắt nhau, ta có:
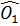 =
= 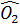 và
và 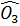 =
= 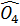 ⇒ OC⊥OD (phân giác của hai góc kề bù)
Vậy
⇒ OC⊥OD (phân giác của hai góc kề bù)
Vậy 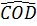 = 90o(đpcm).
b) Theo tính chất của hai tiếp tuyến cắt nhau,
ta có: CA = CM và DB = DM (1)
mà CD = CM + DM ⇒ CD = AC + BD (đpcm).
c) Từ (1) suy ra: AC.BD = MC.MD
mà MC.MD = OM2 = R2 (hệ thức lượng trong tam giác vuông COD đường cao OM).
⇒ AC.BD = R2 = không đổi.
Vậy khi M di chuyển trên nửa đường tròn thì tích AC.BD luôn bằng R2 không đổi (do R không đổi).
= 90o(đpcm).
b) Theo tính chất của hai tiếp tuyến cắt nhau,
ta có: CA = CM và DB = DM (1)
mà CD = CM + DM ⇒ CD = AC + BD (đpcm).
c) Từ (1) suy ra: AC.BD = MC.MD
mà MC.MD = OM2 = R2 (hệ thức lượng trong tam giác vuông COD đường cao OM).
⇒ AC.BD = R2 = không đổi.
Vậy khi M di chuyển trên nửa đường tròn thì tích AC.BD luôn bằng R2 không đổi (do R không đổi).
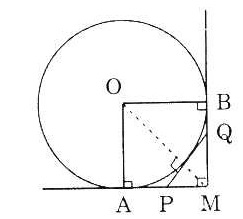
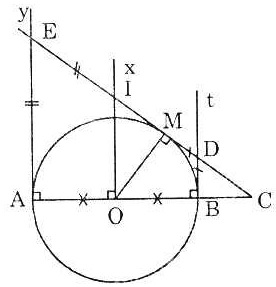
Bài 6. Cho đường tròn tâm O, đường kính AB = 2R, trên tia AB lấy điểm C sao cho BC = 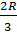 , vẽ tiếp tuyến CM với (O), M là tiếp điểm, kẻ tia Ox vuông góc với AB cắt tia CM tại I, vẽ tiếp tuyến Ay với (O) cắt tia CM tại E. Chứng minh IO = IE. , vẽ tiếp tuyến CM với (O), M là tiếp điểm, kẻ tia Ox vuông góc với AB cắt tia CM tại I, vẽ tiếp tuyến Ay với (O) cắt tia CM tại E. Chứng minh IO = IE. |
|
Giải:
* IO = IE
Vẽ tiếp tuyến Bt với (O) cắt tia CM tại D. Ta có:
BD // OI //AE cùng vuông góc với AB.
Ta còn có: OA = OB = R ⇒ IE = ID = 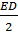 Mà: ED = EM + MD = AE + BD
⇒ ID = IE =
Mà: ED = EM + MD = AE + BD
⇒ ID = IE = 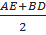 (1)
Hình thang vuông ABDE có OI là đường trung bình
⇒ IO =
(1)
Hình thang vuông ABDE có OI là đường trung bình
⇒ IO = 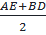 (2)
Từ (1) và (2) suy ra: OI = IE (đpcm).
Bài 7. Cho đường tròn đường kính AB = 2R và hai tiếp tuyến Ax, By và một tiếp tuyến thứ ba (tiếp xúc điểm M), cắt Ax ở C, by ở D.
a) So sánh diện tích
(2)
Từ (1) và (2) suy ra: OI = IE (đpcm).
Bài 7. Cho đường tròn đường kính AB = 2R và hai tiếp tuyến Ax, By và một tiếp tuyến thứ ba (tiếp xúc điểm M), cắt Ax ở C, by ở D.
a) So sánh diện tích  COD và diện tích ACDB.
b) Tìm giá trị nhỏ nhất của hai diện tích trên.
c) Chứng minh AC.BD = R2
Giải:
COD và diện tích ACDB.
b) Tìm giá trị nhỏ nhất của hai diện tích trên.
c) Chứng minh AC.BD = R2
Giải:
a) Ta thấy:  OAC = OAC =  OMC OMC
 OBD = OBD =  OMD OMD
Vậy: 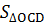 = = 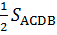
b) 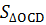 = =  OM.OD; ta thấy OM không đổi; OM.OD; ta thấy OM không đổi;
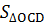 nhỏ nhất khi CD nhỏ nhất khi là giữa hai đường thẳng song song Ax và By (tức là CD = AB = 2R). nhỏ nhất khi CD nhỏ nhất khi là giữa hai đường thẳng song song Ax và By (tức là CD = AB = 2R).
Khi đó: 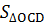 - -  R.2R = R2 R.2R = R2
Hình thang ACDB lúc ấy trở thành hình chữ nhật và diện tích của nó sẽ là2 (gấp đôi diện tích  COD). COD).
c)  COD ( COD (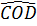 = 90o ); OM là đường cao: = 90o ); OM là đường cao:
OM2 = MC.MD; nhưng MC = AC; MD = BD; OM = R
AC.BD = R2 |
|
© Bản quyền thuộc về
Bài kiểm tra. Ghi rõ nguồn Bài kiểm tra.com khi sao chép nội dung này.