Giải bài tập Hình học 9, chương II: Bài 5: Dấu hiệu nhận biết tiếp tuyến của đường tròn.
2019-08-05T05:00:23-04:00
2019-08-05T05:00:23-04:00
Giải bài tập Hình học 9, chương II: Bài 5: Dấu hiệu nhận biết tiếp tuyến của đường tròn.
/themes/cafe/images/no_image.gif
Bài Kiểm Tra
https://baikiemtra.com/uploads/bai-kiem-tra-logo.png
Thứ hai - 05/08/2019 04:53
Giải bài tập Hình học 9, chương II: Bài 5: Dấu hiệu nhận biết tiếp tuyến của đường tròn.
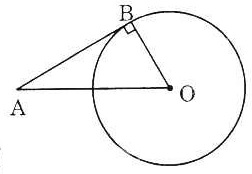
Bài 1. Cho tam giác ABC có AB = 3, AC = 4, BC = 5. Vẽ đường tròn (B, BA) chứng minh rằng AC là tiếp tuyến của đường tròn.
Giải:
Ta có: AB2 = 9; AC2 = 16; BC2 = 25.
Suy ra: BC2 = AB2 + AC2 ⇒  ABC vuông tại A. ABC vuông tại A.
⇒ AC ⊥ BA.
Vậy AC là tiếp tuyến tại A của đường tròn (B; BA). |
|
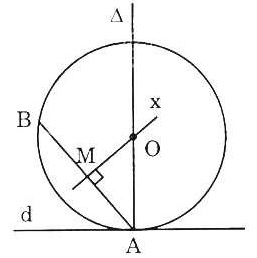
Bài 2. Cho đường thẳng d, điểm A nằm trên đường thẳng d, điểm B nằm ngoài đường thẳng d. Hãy dựng đường tròn (O) đi qua điểm B tiếp xúc với đường thẳng d tại A.
Giải:
Phân tích:
- Đường tròn đi qua hai điểm A, B nên tâm của nó phải nằm trên đường trung trực Mx của đoạn thẳng AB
- Đường thẳng tiếp xúc với đường thẳng d tại điểm A nên tâm của nó phải nằm trên đường thẳng A vuông góc với đường thẳng d tại điểm A.
Vậy O là giao điểm của  với trung trực Mx của AB. với trung trực Mx của AB. |
|
Cách dựng:
- Dựng đường trung trực Mx của AB.
- Dựng đường thẳng A vuông góc với d tại A.
- Dựng giao điểm O của A và Mx.
- Dựng đường tròn tâm O, bán kính OA.
Đó là đường tròn cần dựng.
Chứng minh: O 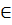 Mx nên đường tròn (O; OA) đi qua A, B. O
Mx nên đường tròn (O; OA) đi qua A, B. O 
 nên đường tròn (O; OA) tiếp xúc với d tại A.
nên đường tròn (O; OA) tiếp xúc với d tại A.
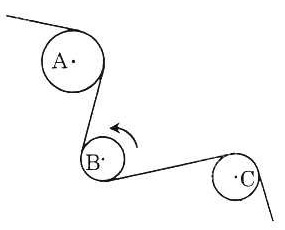
| Bài 3. Đố: Dây cua-roa trên hình bên có những phần là tiếp tuyến của đường tròn tâm A, B, C. Chiều quay của đường tròn tâm b được vẽ trên hình. Tìm chiều quay của đường tròn tâm A và đường tròn tâm C (cùng chiều quay hay ngược chiều quay của kim đồng hồ). |
|
Học sinh tự giải.
BÀI TẬP LÀM THÊM
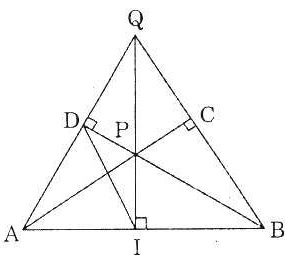
| Bài 1. Cho đường tròn tâm O, dây cung CD. Qua O vẽ đường OH vuông góc với CD tại H, cắt tiếp tuyến tại C của đường tròn ở điểm M. Chứng minh MD là tiếp tuyến của đường tròn. |
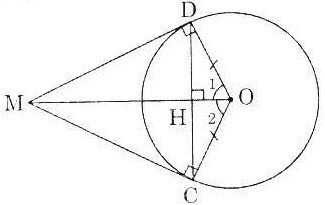 |
Giải:
* Nối OD, xét tam giác cân OCD có OH ⊥ CD.
⇒ HC = HD (tính chất đường kính vuông góc với dây qua trung điểm)
* OH là phân giác nên O1 = O2
*  OCM =
OCM =  ODM (c.g.c) ⇒
ODM (c.g.c) ⇒ 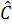 =
= 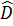 =-90°
Vậy MD là tiếp tuyến với (O) tại D.
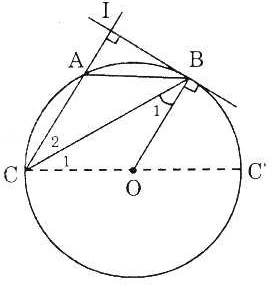
Bài 2. Cho tam giác ABC,
=-90°
Vậy MD là tiếp tuyến với (O) tại D.
Bài 2. Cho tam giác ABC, 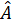 -
- 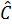 = 90°
a) Chứng minh rằng
= 90°
a) Chứng minh rằng 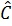 < 45°
b) Chứng minh rằng tiếp tuyến tại B của đường tròn (O) ngoại tiếp
< 45°
b) Chứng minh rằng tiếp tuyến tại B của đường tròn (O) ngoại tiếp  ABC vuông góc với AC tại một điểm I.
c) Chứng minh rằng IB2 = IA.IC
d) Gọi R là bán kính của (O). Chứng minh rằng: AB2 + BC2 =4R2
Hướng dẫn: a) Sử dụng tổng 3 góc của 1 tam giác bằng 180o
b) Để ý rằng IBA = BCA
c) CM:
ABC vuông góc với AC tại một điểm I.
c) Chứng minh rằng IB2 = IA.IC
d) Gọi R là bán kính của (O). Chứng minh rằng: AB2 + BC2 =4R2
Hướng dẫn: a) Sử dụng tổng 3 góc của 1 tam giác bằng 180o
b) Để ý rằng IBA = BCA
c) CM:  IBA
IBA 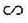
 ICB
d) Dựng đường kính COC’ của (O) và CM: AB = BC’
Giải:
a) Ta có:
ICB
d) Dựng đường kính COC’ của (O) và CM: AB = BC’
Giải:
a) Ta có: 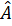 =
= 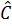 - 90°
⇒
- 90°
⇒ 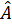 +
+ 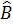 +
+ 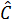 =
= 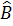 + 2
+ 2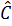 + 90° = 180°
⇒ C = 45o -
+ 90° = 180°
⇒ C = 45o -  < 45o
Vậy
< 45o
Vậy 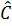 < 45°
b) Ta có:
< 45°
b) Ta có: 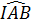 +
+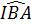 = (180° -
= (180° - 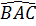 ) +
) + 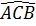 = 180o - (
= 180o - ( 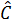 + 90o ) +
+ 90o ) + 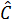 = 90o =
= 90o = 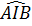 Vậy BI ⊥ AC
Vậy BI ⊥ AC
c) Hai tam giác vuông IBA và IBC có:
 = = 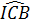 nên đồng dạng nên đồng dạng
 IAB IAB 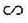  IBC IBC
⇒ 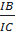 = = 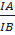 ⇒ IB2 = IA. IC ⇒ IB2 = IA. IC
d) Kẻ đường kính COC’, ta có:
 OBC cân tại O ⇒ OBC cân tại O ⇒ 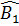 = = 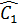
OB //CA (cùng vuông góc với BI) ⇒ 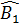 = = 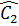
Do đó: 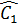 = = 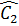 ⇒ ⇒ 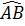 = ' = '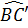 ⇒ AB = BC’ ⇒ AB = BC’
⇒ AB2 + BC2 = BC2+ BC2 = CC’2 = 4R2 |
|
Bài 3. Cho nửa đường tròn tâm O đường kính AB. Kẻ hai dây AC và BD cắt nhau tại một điểm I nằm trong đường tròn. Hạ PI ⊥ AB.
a) CM rằng: 1. BA.BI = BD.BP 2. AB.AI = AC.AP
b) Chứng tỏ rằng: AB2 = AC.AD + BD.BP
c) Hai tia AD và BC gặp nhau tại Q.
Chứng minh 3 điểm Q, B, D thẳng hàng.
Giải:
a) 1. Ta có: 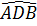 = 90o
Suy ra tứ giác ADPI nội tiếp được:
= 90o
Suy ra tứ giác ADPI nội tiếp được: 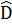 +
+ 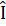 = 90o, hai tam giác BID và BPA có chung nhau góc B và có
= 90o, hai tam giác BID và BPA có chung nhau góc B và có 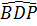 =
= 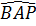 nên đồng dạng:
nên đồng dạng:  BDI
BDI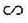
 BAP
⇒
BAP
⇒ 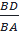 =
= 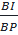 ⇔ BA.BI = BP.BP (1)
2. Tương tự ta có:
⇔ BA.BI = BP.BP (1)
2. Tương tự ta có:  AIC
AIC 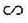
 APB
⇒
APB
⇒ 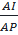 =
= 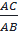 ⇒ AB.AI = AC.AP (2)
⇒ AB.AI = AC.AP (2)
b) Cộng (1) và (2), vế theo vế, ta có:
AB.AI + BA.BI = AC.AP + BD.BP
⇔ AB (AI + BI) = AC.AP + BD.BI
⇔ AB2 = AC.AP + BD.BI
Vậy: AB2 = AC.AP + BD.BI
c) Trong  QAB, AC và BD là hai đường cao nên giao điểm P của AC và BD là trực tâm của QAB, AC và BD là hai đường cao nên giao điểm P của AC và BD là trực tâm của  QAB. QAB.
⇒ QP⊥AB, nhưng PI ⊥ AB. Do đó 3 điểm Q, P, I thẳng hàng. |
|
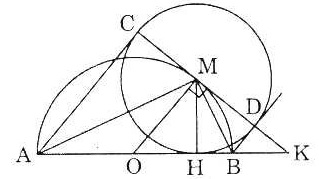
Bài 4. Cho nửa đường tròn (O) đường kính AB = 2R. Gọi M là 1 điểm di động trên (O) (M 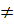 A,B) . Vẽ đường tròn tâm M tiếp xúc với AB tại H. Từ A và B kẻ hai tiếp tuyến tiếp xúc với đường tròn (M) tại C và D.
a) Chứng minh CD là tiếp tuyến của (O).
b) Giả sử CD = 2a. Tính tích BD.AC theo a).
c) Gọi K là giao điểm của CD và AB. Chứng minh OA2 = OB2 = OH.OK.
Giải:
A,B) . Vẽ đường tròn tâm M tiếp xúc với AB tại H. Từ A và B kẻ hai tiếp tuyến tiếp xúc với đường tròn (M) tại C và D.
a) Chứng minh CD là tiếp tuyến của (O).
b) Giả sử CD = 2a. Tính tích BD.AC theo a).
c) Gọi K là giao điểm của CD và AB. Chứng minh OA2 = OB2 = OH.OK.
Giải:
a) Sử dụng tính chất tiếp tuyến ⇒ 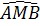 = = 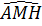 ; ; 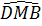 = = 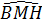 mà mà 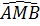 = 90° (do AB là đường kính (O), M = 90° (do AB là đường kính (O), M 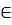 (O)) (O))
⇒ CMD = 180o
⇒ C, M, D thẳng hàng.
OM là đường trung bình hình thang.
ABCD OM ⊥ CD (đpcm)
b) AC.BD - AH.HB = MH2 = a2
c)  OMK vuông tại M. Có MH là đường cao ⇒ OH.OK = OM2 OMK vuông tại M. Có MH là đường cao ⇒ OH.OK = OM2 |
|
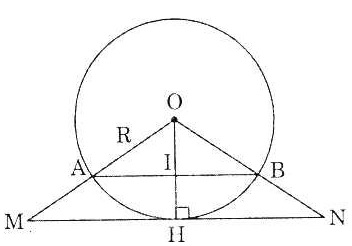
Bài 5. Cho đường tròn (O; R) và dây AB = 1,6R. Vẽ một tiếp tuyến song với AB, nó cắt các tia OA và OB theo thứ tự tại M và N. Tính diện tích  MON.
Giải:
MON.
Giải:
Nối OH ta được OH ⊥ MN (tính chất của tiếp tuyến). Ta lại có AB // MN (gt) nên OH ⊥ AB (tại I).
Theo tính chất dường kính vuông góc với một dây ta được:
IA = IB = 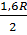 = 0,8R = 0,8R
Áp dụng định lí Pitago vào tam giác vuông IOA ta được:
OI2 = OA2 – IA2 = R2 - (0,8R)2 - 0,36R2 ⇒ OI = 0,6R
Xét  OMN có AB // MN (gt) ⇒ OMN có AB // MN (gt) ⇒  OAB OAB 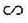  OMN OMN
⇒ 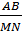 = = 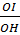 (tỉ số hai đường cao tương ứng bằng tỉ số đồng dạng) (tỉ số hai đường cao tương ứng bằng tỉ số đồng dạng)
Vậy: MN = 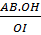 = =  = =  R R
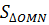 = =  MN.OH = MN.OH =  . .  R.R = R.R =  R2 R2 |
 |
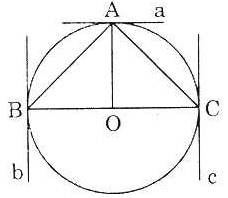
Bài 6. Cho  ABC vuông cân tại A.
a) Hãy nêu cách dựng tiếp tuyến a của đường tròn ngoại tiếp
ABC vuông cân tại A.
a) Hãy nêu cách dựng tiếp tuyến a của đường tròn ngoại tiếp  ABC, biết tiếp tuyến đi qua điểm A. Chứng minh rằng a // BC.
b) Hãy nêu cách dựng các tiếp tuyến b, c của đường tròn ngoại tiếp
ABC, biết tiếp tuyến đi qua điểm A. Chứng minh rằng a // BC.
b) Hãy nêu cách dựng các tiếp tuyến b, c của đường tròn ngoại tiếp  ABC, biết rằng các tiếp tuyến này theo thứ tự đi qua điểm B, C. Chứng minh rằng b // c.
Giải:
ABC, biết rằng các tiếp tuyến này theo thứ tự đi qua điểm B, C. Chứng minh rằng b // c.
Giải:
Vì  ABC vuông cân tại A nên đường tròn ngoại tiếp ABC vuông cân tại A nên đường tròn ngoại tiếp  ABC có tâm O là trung điểm của BC. ABC có tâm O là trung điểm của BC.
a) Tiếp tuyến qua A là đường thẳng C a qua A và vuông góc với OA.
Vì OA ⊥ BC nên a // BC (đpcm).
b) Ta có ngay:
- Tiếp tuyến qua R là đường thẳng b qua B và vuông góc với BC.
- Tiếp tuyến qua C là đường thẳng C qua C và vuông góc với BC. Từ đó ⇒ b //c (đpcm). |
 |
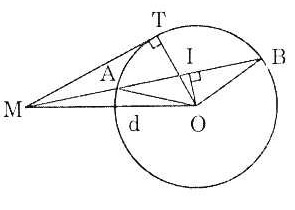
Bài 7. Cho đường tròn tâm O bán kính R cố định, M là một điểm cố định nằm ngoài đường tròn sao cho OM = d > R.
Một đường thẳng (d) quay quanh M cắt đường tròn (O) tại 2 điểm A và B.
a) Chứng minh rằng: MA.MB = d2 – R2
b) Định vị trí của (d) để MA + MB nhỏ nhất và lớn nhất.
Giải:
a) Gọi I là trung điểm của AB.
Ta có: MI = 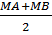
⇔ MA + MB = 2MI
⇔(MA + MB)2 = 4MI2
⇔ (MA + MB)2 = 4 (OM2 – OI2) (1)
Mặt khác: MB - MA = AB = 2AI
⇔ ( MB – MA)2 = 4AI2 = 4 (OA2 – OI2 ) (2 )
(1) - (2) ⇒ 4 MA.MB - 4 (OM2 – OA2)
⇔ MA.MH = OM2 – OA2 = d2 – R2
b) Vẽ tiếp tuyến MT với đường tròn:
 MIO vuông ⇒ MI MIO vuông ⇒ MI 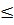 OM (*) OM (*)
và MI2 – OM2 – OI2 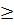 OM2 – OT2 (vì OI < OT = R ) OM2 – OT2 (vì OI < OT = R )
 OMT vuông: MT2 = OM2 – OT2 OMT vuông: MT2 = OM2 – OT2
⇒ MI2 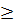 MT2 ⇔ MI MT2 ⇔ MI 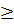 MT (**) MT (**)
Dấu bằng xảy ra ⇔ I = T.
(*) và (**) ⇒ MT 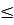 MI MI 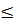 OM OM
⇔ 2MT 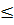 2MI 2MI 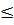 20M 20M
⇔ 2MT 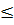 MA + MB MA + MB 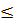 OM OM
Vậy:
* MA + MB đạt giá trị nhỏ nhất khi MAB là tiếp tuyến (MA + MB = 2MT).
* MA + MB đạt giá trị lớn nhất khi MAB qua tâm O (MA + MB = 2OM) |
|
© Bản quyền thuộc về
Bài kiểm tra. Ghi rõ nguồn Bài kiểm tra.com khi sao chép nội dung này.