Giải bài tập Hình học 9, chương II: Bài 4: Vị trí tương đối của đường thẳng và đường tròn.
2019-08-04T23:17:00-04:00
2019-08-04T23:17:00-04:00
Giải bài tập Hình học 9, chương II: Bài 4: Vị trí tương đối của đường thẳng và đường tròn.
/themes/cafe/images/no_image.gif
Bài Kiểm Tra
https://baikiemtra.com/uploads/bai-kiem-tra-logo.png
Chủ nhật - 04/08/2019 23:14
Giải bài tập Hình học 9, chương II: Bài 4: Vị trí tương đối của đường thẳng và đường tròn.
Bài 1. Điền vào các chỗ trống (...) trong bảng sau (R là bán kính của đường tròn, d là khoảng cách từ tâm đến đường thẳng):
| R |
d |
Vị trí tương đối của đường thẳng và đường tròn |
5cm
6cm
4cm |
3cm
……
7cm |
……
Tiếp xúc nhau
……. |
Giải:
| R |
d |
Vị trí tương đối của đường thẳng và đường tròn |
5cm
6cm
4cm |
3cm
6cm
7cm |
Đường thẳng cắt đường tròn (d < R)
Đường thẳng tiếp xúc với đường tròn (d = R)
Đường thẳng và đường tròn không giao nhau (d > R) |
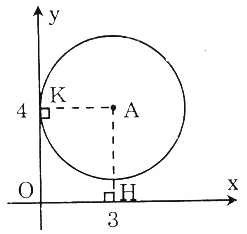
Bài 2. Trên mặt phẳng tọa độ Oxy, cho điểm A(3; 4). Hãy xác định vị trí tương đối của đường tròn (A; 3) và các trục tọa độ.
Giải:
+ Hạ AH ⊥ Ox
Ta có: AH |XA| = 4 ⇒ AH > R.
Vậy Ox và đường tròn (A; 3) không giao nhau.
+ Hạ AH ⊥ Oy.
Ta có: AK = |yA| = 3 ⇒ AK = R.
Vậy Oy tiếp xúc với đường tròn (A; 3). |
|
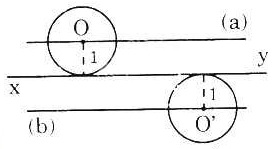
Bài 3. Cho đường thẳng xy. Tâm cua các đường tròn có bán kính 1cm và tiếp xúc với đường thẳng xy nằm trên đường nào?
Giải:
Gọi O là tâm của một đường tròn bất kì có bán kính bằng 1cm và tiếp xúc với đường thẳng xy.
Theo đề bài ta có: d = R.
Vì tâm O cách đường thẳng xy cố định 1cm nên O nằm trên các đường thẳng (a) và (b) song song với xy và cách xy một khoảng là 1cm. |
 |
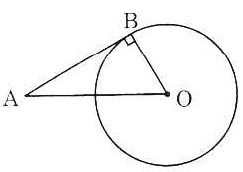
Bài 4. Cho đường tròn tâm O bán kính 6cm và một điểm A cách O là 10cm. Kẻ tiếp tuyến AB với đường tròn (B là tiếp điểm). Tính độ dài AB.
Giải:
Tam giác OAB vuông tại B nên:
AB2 = OA2 – OB2 = 102 – 62 = 64
⇒ AB = 8. |
|
BÀI TẬP LÀM THÊM
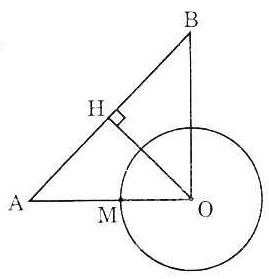
Bài 1. Cho đường tròn tâm O, bán kính R = 2. M là một điểm trên đương tròn, kéo dài OM một đoạn MA = OM. Dựng tam giác AOB vuông tại O, xét vị trí tương đối của đường thẳng AB với đường tròn (O) biết:
a) tgA =  b) tgA =
b) tgA = 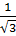 c) tgA =
c) tgA = 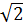 Giải:
Ta có: OA = OM + MA = 2 + 2 = 4
Dựng OA ⊥AB, tam giác AOB vuông tại O
⇒ OB = OA.tgA
a) Với tgA =
Giải:
Ta có: OA = OM + MA = 2 + 2 = 4
Dựng OA ⊥AB, tam giác AOB vuông tại O
⇒ OB = OA.tgA
a) Với tgA =  , ta có OB = 4.
, ta có OB = 4. = 2
Tam giác AOB vuông tại O, có OH là đường cao nên:
= 2
Tam giác AOB vuông tại O, có OH là đường cao nên:
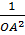 =
= 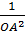 +
+ 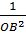 =
= 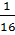 +
+  =
= 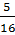 ⇒ OH2 =
⇒ OH2 = 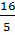 ⇒ OA =
⇒ OA = 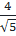
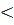 2
⇒ OH < R
Vậy AB cắt đường tròn (O) tại hai điểm.
b) Với tgA =
2
⇒ OH < R
Vậy AB cắt đường tròn (O) tại hai điểm.
b) Với tgA = 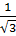 , ta có: OB = 4.
, ta có: OB = 4.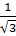 =
= 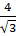 Mặt khác:
Mặt khác:
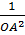 =
= 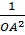 +
+ 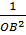 =
= 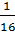 +
+ 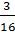 =
= 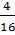 =
=  ⇒ OA2 = 4 ⇒ OA = 2 ⇒ OA = R
Vậy AB tiếp xúc với đường tròn (O) tại A.
⇒ OA2 = 4 ⇒ OA = 2 ⇒ OA = R
Vậy AB tiếp xúc với đường tròn (O) tại A.
c) Với tgA = 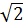 ta có: OB = 4 ta có: OB = 4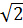
Mặt khác:
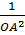 = = 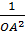 + + 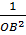 = = 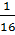 + + 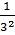 = = 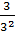
⇒ OA2 = 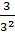 ⇒ OA = ⇒ OA = 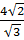 > 2 > 2
⇒ OH > R
Vậy: AB không cắt đường tròn (O). |
|
Bài 2. Cho hai đường tròn (O) và (O’) cắt nhau tại A và R. Qua A, vẽ một đường thẳng tùy ý (tức di động quanh A), đường tháng này cắt (O) tại C và cắt (O’) tại D. Gọi M, N lần lượt là trung điểm AC và AD.
a) Chứng minh rằng MN =  CD.
b) Nêu cách dựng đoạn thẳng CD đi qua A với O trên (O) và D trên (O’) sao cho CD = 2d cho trước.
c) Gọi I là trung điểm MN. Chứng minh rằng đường thẳng vuông góc CD tại I đi qua điểm cố định. Hãy giải thích cách vẽ CD trong bài này để CD nhận A làm trung điểm.
Giải:
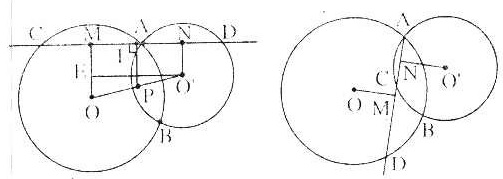
a) Phải xét hai trường hợp để chứng minh: Trường hợp A nằm trong và trường hợp A nằm ngoài đoạn thẳng CD như hình vẽ dưới đây.
b) Giả sử dựng được đoạn thẳng CD = 2d như đề bài. Từ O’ kẻ OE // CD. Ta có MNO’E là hình chữ nhật và O’E = MN = d. Suy ra cách dựng: Dựng đường tròn đường kính OO’ và đường tròn tâm O’ bán kính d. Khi đó:
- Nếu d < OO’ thì hai đường tròn nói trên cắt nhau tại E và F. Từ A, ta kẻ các đường thẳng song song O’E và O’F. Hai đường thẳng này cắt đường tròn (O) và (O’), tạo thành hai đoạn thẳng CD và C’D’ cần dựng.
Thật vậy, ta có CD = 2O’E = 2d và C’D’ = 2O’F = 2d.
- Nếu d = OO’, hai đường tròn nối trên tiếp xúc trong với nhau tại O. Trong trường hợp này, ta có duy nhất đoạn thẳng CD do đường đi qua A và song song OO’ tạo thành.
- Nếu d > OO’. hai đường tròn nói trên không cắt nhau, bài toán không có nghiệm hình.
c) Ta có OMNO’ là hình thang vuông. Gọi P là trung điểm OO’ thì P là điểm cố định. Rõ ràng IP là đoạn thẳng nối trung điểm hai cạnh bên của hình thang vuông, nên IP ⊥ MN. Nói cách khác, đường thẳng vuông góc CD tại I đi qua một điểm cố định, đó là P. Nếu CD nhận A làm trung điểm thì MN cũng vậy, nghĩa là A phải trùng I. Từ đó, để vẽ CD thỏa mãn đề bài, ta chỉ cần nối AP, rồi vẽ qua A đường thẳng vuông góc AP, sẽ có được CD.
CD.
b) Nêu cách dựng đoạn thẳng CD đi qua A với O trên (O) và D trên (O’) sao cho CD = 2d cho trước.
c) Gọi I là trung điểm MN. Chứng minh rằng đường thẳng vuông góc CD tại I đi qua điểm cố định. Hãy giải thích cách vẽ CD trong bài này để CD nhận A làm trung điểm.
Giải:
a) Phải xét hai trường hợp để chứng minh: Trường hợp A nằm trong và trường hợp A nằm ngoài đoạn thẳng CD như hình vẽ dưới đây.
b) Giả sử dựng được đoạn thẳng CD = 2d như đề bài. Từ O’ kẻ OE // CD. Ta có MNO’E là hình chữ nhật và O’E = MN = d. Suy ra cách dựng: Dựng đường tròn đường kính OO’ và đường tròn tâm O’ bán kính d. Khi đó:
- Nếu d < OO’ thì hai đường tròn nói trên cắt nhau tại E và F. Từ A, ta kẻ các đường thẳng song song O’E và O’F. Hai đường thẳng này cắt đường tròn (O) và (O’), tạo thành hai đoạn thẳng CD và C’D’ cần dựng.
Thật vậy, ta có CD = 2O’E = 2d và C’D’ = 2O’F = 2d.
- Nếu d = OO’, hai đường tròn nối trên tiếp xúc trong với nhau tại O. Trong trường hợp này, ta có duy nhất đoạn thẳng CD do đường đi qua A và song song OO’ tạo thành.
- Nếu d > OO’. hai đường tròn nói trên không cắt nhau, bài toán không có nghiệm hình.
c) Ta có OMNO’ là hình thang vuông. Gọi P là trung điểm OO’ thì P là điểm cố định. Rõ ràng IP là đoạn thẳng nối trung điểm hai cạnh bên của hình thang vuông, nên IP ⊥ MN. Nói cách khác, đường thẳng vuông góc CD tại I đi qua một điểm cố định, đó là P. Nếu CD nhận A làm trung điểm thì MN cũng vậy, nghĩa là A phải trùng I. Từ đó, để vẽ CD thỏa mãn đề bài, ta chỉ cần nối AP, rồi vẽ qua A đường thẳng vuông góc AP, sẽ có được CD.
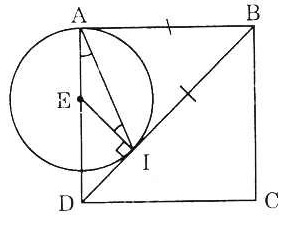
Bài 3. Cho hình vuông ABCD, trên đường chéo BD lấy điểm I sao cho BI = BA.
Đường thẳng kẻ qua I vuông góc với BD cắt AD tại E.
a) So sánh các đoạn thẳng AE, EI, ID.
b) Xác định vị trí tương đối cua đường thẳng BD với đường tròn (E; EA). |
|
Giải:
Tam giác ABI cân ở B nên:
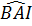 =
= 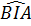 ⇒
⇒ 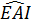 =
= 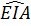 Tam giác AEI cân ở E, ta có EA = EI (1)
Tam giác IDE vuông cân ở I, ta có IE = ID (2)
Từ (1) và (2) suy ra: EA = EI = ID
Tam giác AEI cân ở E, ta có EA = EI (1)
Tam giác IDE vuông cân ở I, ta có IE = ID (2)
Từ (1) và (2) suy ra: EA = EI = ID
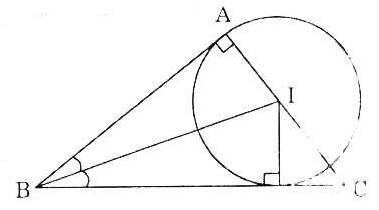
Bài 4. Cho  ABC vuông cân tại A. Vẽ phân giác BI. ABC vuông cân tại A. Vẽ phân giác BI.
a) Chứng minh rằng đường tròn (I; IA) tiếp xúc với các đường thẳng AB và BC.
b) Cho biết AB = a, tính IA từ đó suy ra tg22o30’ = 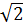 - 1 - 1 |
|
Giải:
a) Ta có: IA ⊥ BA ⇔ IA = d(I,BA)
⇔ (I, IA) tiếp xúc với BA tại A.
Mặt khác: BI là phân giác góc 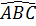 .
Do đó (I, IA) tiếp xúc với BC.
b) Sử dụng tính chất của tia phân giác trong
.
Do đó (I, IA) tiếp xúc với BC.
b) Sử dụng tính chất của tia phân giác trong  ABC, ta có:
ABC, ta có:
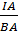 =
= 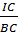 =
= 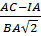 ⇔
⇔ 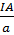 =
= 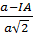 ⇔
⇔ 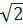 IA = a – IA ⇔ IA =
IA = a – IA ⇔ IA = 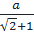 – a (
– a (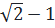 )
Khi đó, trong
)
Khi đó, trong  ABI vuông tại A, ta có:
tg
ABI vuông tại A, ta có:
tg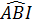 =
= 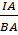 ⇔ tg22o30’=
⇔ tg22o30’= 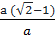 =
= 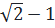 (đpcm)
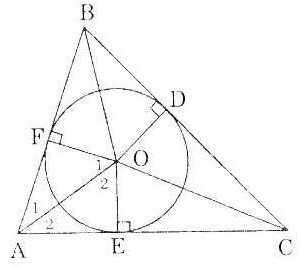
Bài 5. Chứng minh rằng giao điểm của ba đường phân giác trong một tam giác là tâm của một đường tròn tiếp xúc với ba cạnh của tam giác (gọi là đường tròn nội tiếp tam giác hoặc tam giác ngoại tiếp đường tròn).
Giải:
(đpcm)
Bài 5. Chứng minh rằng giao điểm của ba đường phân giác trong một tam giác là tâm của một đường tròn tiếp xúc với ba cạnh của tam giác (gọi là đường tròn nội tiếp tam giác hoặc tam giác ngoại tiếp đường tròn).
Giải:
Tam giác ABC có ba đường phân giác giao nhau tại O. Từ O kẻ OE, OF, OD lần lượt vuông góc với AC, AB, BC.
Xét tam giác  AEO và AEO và  AFO có: AFO có:
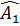 = = 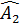 (gt) (gt)
AO : cạnh chung
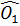 - - 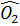 ( (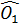 = 90o = = 90o = 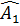 = 90o - = 90o - 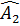 = = 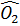 ) )
⇒  AEO = AEO =  AFO (g.c.g) ⇒ OE = OF AFO (g.c.g) ⇒ OE = OF
Tương tự  BFO = BFO =  BDO ⇒ OF - OD BDO ⇒ OF - OD
Suy ra OD = OE = OF nên O cách đều ba cạnh của tam giác. Vậy đường tròn (O; OP) qua 3 điểm D, E, F và tiếp xúc với ba cạnh của tam giác ABC.
b) Ta có: EI = EA = ED
⇒ I 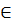 (E, EA) ⇒ R = EI (E, EA) ⇒ R = EI
Mặt khác: EI = BD nên d = EI ⇒ d = R
Vậy đường thẳng BD tiếp xúc với đường tròn (E, EA). |
|
© Bản quyền thuộc về
Bài kiểm tra. Ghi rõ nguồn Bài kiểm tra.com khi sao chép nội dung này.