Giải bài tập Hình học 9, chương II: Bài 3: Liên hệ giữa dây và khoảng cách từ tâm đến dây.

Chủ nhật - 04/08/2019 04:20

Giải bài tập Hình học 9, chương II: Bài 3: Liên hệ giữa dây và khoảng cách từ tâm đến dây.

Bài 1. Cho đường tròn tâm O bán kính 5cm, dây AB bằng 8cm.
a) Tính khoảng cách từ tâm O đến dây AB.
b) Gọi I là điểm thuộc dây AB sao cho AI = 1cm. Kẻ dây CD đi qua I và vuông góc với AB. Chứng minh rằng CD = AB.

Giải:

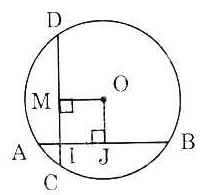
a) Gọi J là trung điểm của AB ⇒ OJ

AB
Hay OJ là khoảng cách từ tâm O đến dây AB. Trong tam giác vuông AJO thì:
OJ² = OA² – AJ² = 5² – 4² = 9
⇒ OJ = 3.

b) Gọi M là trung điểm của CD ⇒ OM

CD.
Tứ giác OMIJ có ba góc vuông và IJ = OJ (= 3) nên nó là hình vuông.
Do đó: OM = OJ.
Hai dây AB và CD cách đều tâm O AB = CD (đpcm).

Bài 2. Cho đường tròn (O) có dây AB và CD bằng nhau, các tia AB và CI) cắt nhau tại điếm E nằm bên ngoài đường tròn. Gọi H và K theo thứ tự là trung điểm của AB và CD. Chứng minh rằng:
a) EH = EK; b) EA = EC

Giải:

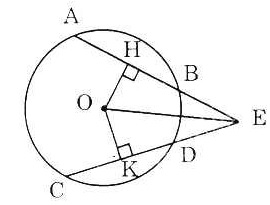
a) Trong đường tròn (O), ta có AB = CD (gt)
⇒ OH = OK (hai dây cung bằng nhau thì cách đều tâm đường tròn )
Xét hai tam giác vuông OEH và OEK, ta có:
OK = OH (cmt)
OE: cạnh huyền chung.
Vậy

OEH =

OEK
Suy ra EH = EK (đpcm) (1)

b) Vì OH ⊥ AB nên HA = HB =

và OK ⊥ CD nên KC = KD =

Suy ra HA = KC (2)
Lấy (1) cộng với (2) theo vế, ta có:
EH + HA = EK + KC hay EA = EC (đpcm).

Ý kiến bạn đọc

Theo dòng sự kiện

Xem tiếp...

Những tin mới hơn

Những tin cũ hơn

THÀNH VIÊN

BÀI LUYỆN THI

Lớp 1	Lớp 2	Lớp 3	Lớp 4	Lớp 5
Lớp 6	Lớp 7	Lớp 8	Lớp 9
Lớp 10	Lớp 11	Lớp 12
Kiểm tra 15 phút		Kiểm tra 1 tiết
Kiểm tra học kì 1		Kiểm tra học kì 2
Luyện thi theo Bài học
Luyện thi THPT Quốc Gia

Giải bài tập Hình học 9, chương II: Bài 3: Liên hệ giữa dây và khoảng cách từ tâm đến dây.

Giải bài tập Hình học 9, chương II: Bài 3: Liên hệ giữa dây và khoảng cách từ tâm đến dây.

Nếu không được bước tiếp trên con đường học vấn, anh (chị) sẽ chọn nghề gì? (14/10/2019)

Tin học THCS Quyển 4, Bài thực hành 11. Tạo video ngắn bằng Movie Maker (14/10/2019)

Tin học THCS Quyển 4, Bài 14. Thiết kế phim bằng phần mềm Movie Maker (14/10/2019)

Tin học THCS Quyển 4, Bài thực hành 10. Tạo sản phẩm âm thanh bằng Audacity (14/10/2019)

Tin học THCS Quyển 4, Bài 13. Phần mềm ghi âm và xử lý âm thanh Audacity (14/10/2019)

Tin học THCS Quyển 4, Bài 12. Thông tin đa phương tiện (13/10/2019)

Tin học THCS Quyển 4, Bài thực hành 9. Thực hành tổng hợp (13/10/2019)

Tin học THCS Quyển 4, Bài thực hành 8. Hoàn thiện bài trình chiếu với hiệu ứng động (13/10/2019)

Tin học THCS Quyển 4, Bài 11. Tạo các hiệu ứng động (13/10/2019)

Tin học THCS Quyển 4, Bài thực hành 7. Trình bày thông tin bằng hình ảnh (13/10/2019)

Giải bài tập Hình học 9, luyện tập liên hệ giữa dây và khoảng cách từ tâm đến dây. (04/08/2019)

Giải bài tập Hình học 9, chương II: Bài 4: Vị trí tương đối của đường thẳng và đường tròn. (04/08/2019)

Giải bài tập Hình học 9, chương II: Bài 5: Dấu hiệu nhận biết tiếp tuyến của đường tròn. (05/08/2019)

Giải bài tập Hình học 9, luyện tập dấu hiệu nhận biết tiếp tuyến của đường tròn. (05/08/2019)

Giải bài tập Hình học 9, chương II: Bài 6: Tính chất của hai tiếp tuyến cắt nhau (06/08/2019)

Giải bài tập Hình học 9, luyện tập tính chất của hai tiếp tuyến cắt nhau. (06/08/2019)

Giải bài tập Hình học 9, chương II: Bài 7: Vị trí tương đối của hai đường tròn. (06/08/2019)

Giải bài tập Hình học 9, luyện tập vị trí tương đối của hai đường tròn. (06/08/2019)

Giải bài tập Hình học 9: Ôn tập chương II (06/08/2019)

Giải bài tập Toán 9, chương III, bài 1: Phương trình bậc nhất hai ẩn. (20/08/2019)

Giải bài tập Hình học 9, chương II: Bài 2: Đường kính và dây của đường tròn. (04/08/2019)

Giải bài tập Hình học 9, Luyện tập sự xác định đường tròn, tính chất đối xứng của đường tròn. (04/08/2019)

Giải bài tập Hình học 9, chương II: Bài 1: Sự xác định đường tròn, tính chất đối xứng của đường tròn. (03/08/2019)

Giải bài tập Hình học 9: Ôn tập chương I. (03/08/2019)

Giải bài tập Hình học 9, luyện tập một số hệ thức về cạnh và góc trong tam giác vuông. (02/08/2019)

Giải bài tập Hình học 9, chương I: Bài 4: Một số hệ thức về cạnh và góc trong tam giác vuông. (02/08/2019)

Giải bài tập Hình học 9, luyện tập bảng lượng giác (02/08/2019)

Giải bài tập Hình học 9, chương I: Bài 3: Bảng lượng giác (02/08/2019)

Giải bài tập Hình học 9: Luyện tập tỉ số lượng giác của góc nhọn (02/08/2019)

Giải bài tập Hình học 9, chương I: Bài 2: Tỉ số lượng giác của góc nhọn (02/08/2019)