Giải bài tập Hình học 9, chương II: Bài 2: Đường kính và dây của đường tròn.
2019-08-04T04:11:52-04:00
2019-08-04T04:11:52-04:00
Giải bài tập Hình học 9, chương II: Bài 2: Đường kính và dây của đường tròn.
/themes/cafe/images/no_image.gif
Bài Kiểm Tra
https://baikiemtra.com/uploads/bai-kiem-tra-logo.png
Chủ nhật - 04/08/2019 04:11
Giải bài tập Hình học 9, chương II: Bài 2: Đường kính và dây của đường tròn.
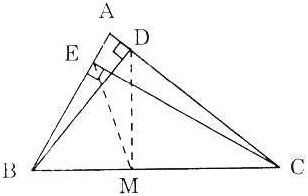
Bài 1. Cho tam giác ABC, các đường cao BD và CE. Chứng minh rằng:
a) Bốn điểm B, D, E, C cùng thuộc một đường tròn.
b) DE < BC.
Giải:
a) Gọi M là trung điểm của cạnh BC.
Trong tam giác vuông BDC,
ta có: MD =  BC. BC.
Trong tam giác vuông BEC,
ta có: ME =  BC. BC.
Do đó: MB = ME = MD = MC.
Suy ra: M cách đều bốn điểm B, E, D, C vậy bốn điểm A, B, D, C nằm trên đường tròn tâm M, bán kính bằng  BC. BC.
b) Trong dường tròn đường kính BC thì DE là một dây, BC là đường kính nên DE < BC. |
|
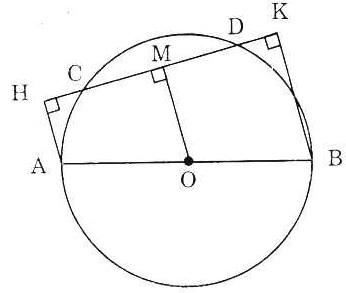
Bài 2. Cho đường tròn (O) đường kính AB, dây CD không cắt đường kính AB. Gọi H và K theo thứ tự là chân các đường vuông góc kẻ từ A và B đến CD. Chứng minh rằng CH = DK.
Gợi ý: Kẻ OM vuông góc với CD.
Giải:
Kẻ OM ⊥ CD thì M là trung điểm của CD, cho ta:
MC = MD (1)
Ta có: 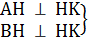 ⇒ AH // BK ⇒ AH // BK
⇒ ABKH là hình thang.
Ta cùng có OM // AH và O là trung điểm của AB nên M là trung điểm của HK, cho ta:
MH = MK (2)
Từ (1) và (2) suy ra đpcm. |
|
© Bản quyền thuộc về
Bài kiểm tra. Ghi rõ nguồn Bài kiểm tra.com khi sao chép nội dung này.