Giải bài tập Hình học 9, chương II: Bài 1: Sự xác định đường tròn, tính chất đối xứng của đường tròn.
2019-08-03T23:47:40-04:00
2019-08-03T23:47:40-04:00
Giải bài tập Hình học 9, chương II: Bài 1: Sự xác định đường tròn, tính chất đối xứng của đường tròn.
/themes/cafe/images/no_image.gif
Bài Kiểm Tra
https://baikiemtra.com/uploads/bai-kiem-tra-logo.png
Thứ bảy - 03/08/2019 23:44
Giải bài tập Hình học 9, chương II: Bài 1: Sự xác định đường tròn, tính chất đối xứng của đường tròn.
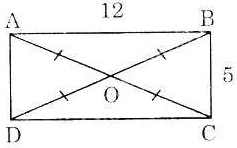
Bài 1. Cho hình chữ nhật ABCD có AB = 12cm. BC = 5cm. Chứng minh rằng bốn điểm A, B, C, D thuộc cùng một đường tròn, tính bán kính của đường tròn đó.
Giải:
Gọi O là giao điểm của hai đường chéo AC và BD của hình chữ nhật ABCD.
Suy ra OA = OB = OC = OD
Vậy 4 điểm A, B, C, D thuộc cùng một đường tròn (tâm O, bán kính OA)
Trong tam giác vuông ABC (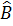 = 90o), ta có: = 90o), ta có:
AC2 = AB2 + AC2
⇒ AC = 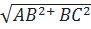 = = 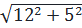 = = 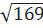 = 13 (cm) = 13 (cm)
⇒ OA = 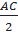 = = 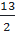 = 6,5 (cm) = 6,5 (cm)
Vậy bán kính của đường tròn bằng 6,5cm |
|
Bài 2. Hãy nối mỗi ô ở cột trái với một ô ở cột phải để được khẳng định đúng:
| (1) Nếu tam giác có ba góc nhọn |
(4) thì tâm của đường tròn ngoại tiếp tam giác đó nằm bên ngoài tam giác. |
| (2) Nếu tam giác có góc vuông |
(5) thì tâm của đường tròn ngoại tiếp tam giác đó nằm bên trong tam giác. |
| (3) Nếu tam giác có góc tù |
(6) thì tâm của đường tròn ngoại tiếp tam giác đó là trung điểm của cạnh lớn nhất. |
| |
(7) thì tâm của đường tròn ngoại tiếp tam giác đó là trung điểm của cạnh nhỏ nhất. |
Giải:
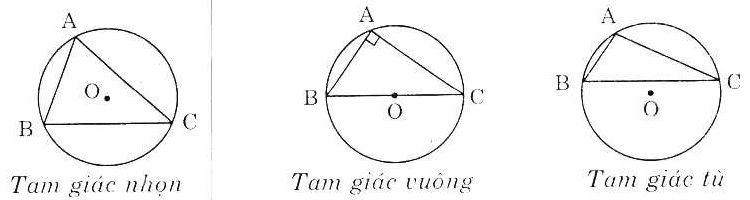 Như vậy: Nối (1) với (5) ; (2) với (6); (3) với (4)
Bài 3. Chứng minh các định lý sau:
a) Tâm của đường tròn ngoại tiếp tam giác vuông là trung điểm của cạnh huyền.
b) Nếu một tam giác có một cạnh là đường kính của đường tròn ngoại tiếp thì tam giác đó là tam giác vuông.
Giải:
Như vậy: Nối (1) với (5) ; (2) với (6); (3) với (4)
Bài 3. Chứng minh các định lý sau:
a) Tâm của đường tròn ngoại tiếp tam giác vuông là trung điểm của cạnh huyền.
b) Nếu một tam giác có một cạnh là đường kính của đường tròn ngoại tiếp thì tam giác đó là tam giác vuông.
Giải:
a) Giả sử tam giác ABC vuông tại A; O là trung điểm cạnh huyền BC.
Trong tam giác vuông ABC thì trung tuyến AO =  BC hay OA = OB = OC. BC hay OA = OB = OC.
Vậy O chính là tâm đường tròn ngoại tiếp tam giác ABC.
b) Giả sử đường tròn ngoại tiếp tam giác ABC có dường kính là BC. Khi đó gọi O là trung điểm của bC thì O là tâm đường tròn này.
⇒ OA, OB, OC là các bán kính của đường tròn
⇒ OA = OB = OC =  BC. BC.
Tam giác ABC có trung tuyến AO bằng một nửa cạnh đối diện. Vậy nó là tam giác vuông tại A. |
 |
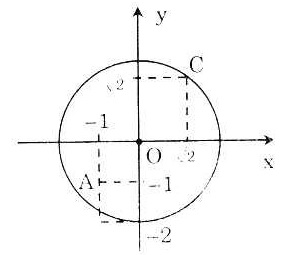
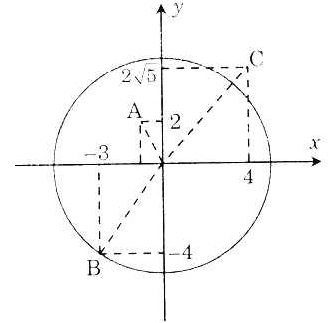
Bài 4. Trên mặt phăng tọa độ Oxy. hãy xác định vị trí cua mỏi điểm A(-1; -1), B (-1; -2); C(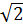 ;
;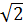 ) đối với đường tròn tâm O bán kính 2.
Giải:
) đối với đường tròn tâm O bán kính 2.
Giải:
Ta có: OA2 = 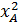 + +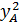 = (-1)2+ (-1)2 = 2 = (-1)2+ (-1)2 = 2
⇒ OA = 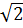 < R < R
⇒ A nằm trong đường tròn.
Tương tự:
* OB = 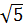 > R ⇒ B nằm ngoài đường tròn. > R ⇒ B nằm ngoài đường tròn.
* OC = 2 ⇒ C nằm trên đường tròn. |
|
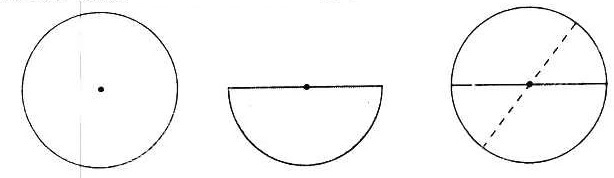
Bài 5. Đố: Một tấm bìa hình tròn không còn dấu vết của tâm tìm lại tâm của hình tròn đó.
Giải:
Gấp tấm bìa sao cho hai nửa chồng khít với nhau. Nếp gấp là một đường kính. Gấp tấm bìa theo một đường thẳng khác sao cho hai nửa chồng khít lên nhau. Ta được một đường kính thứ hai. Giao của hai đường kính này là tâm của hình tròn.
BÀI TẬP LÀM THÊM
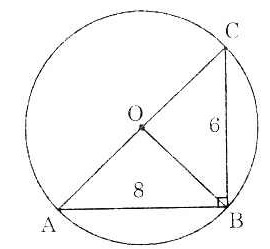
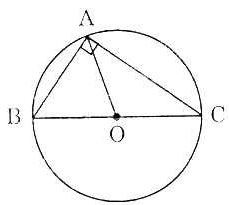
Bài 1. Cho đường tròn (O), dây AB, vẽ dây BC vuông góc với AB.
a) Chứng minh AO là đường kính của đường tròn (O).
b) Tính bán kính đường tròn (O), biết AB = 8cm. BC = 6cm.
Giải:
a) Tam giác AOB cân ở O, ta có:
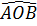 = 180o - 2 = 180o - 2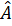
Tam giác BOC cân ở O, ta có:
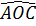 = = 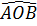 + + 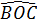
= 360o + 2.(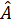 + + 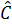 ) )
= 360o + 2.90o = 180o
Do đó ba điểm A, O, C thẳng hàng
Suy ra AO là đường kính của đường tròn (O).
b) Tam giác ABC vuông ở B:
AC2 = AB2 + BC2 = 82 + 62 = 100
Suy ra AC = 10 (cm).
Vậy bán kính đường tròn (O) là 5cm
Vậy bán kính đường tròn (O) là R = 5cm |
|
Bài 2. Cho đường tròn tâm O, bán kính R= 5. Hãy xác định vị trí của mỗi điểm A, B, C đối với đường tròn, biết A(-1, 2), B(3, - 4), C(4; 2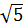 )
Giải:
)
Giải:
A(-1, 2), ta có:
OA2 = 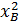 + +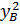 = (-1)2 + 22 = 5 ⇒ OA = = (-1)2 + 22 = 5 ⇒ OA = 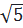 < 5 ⇒ OA < R < 5 ⇒ OA < R
Vậy A nằm trong đường tròn.
B(-3, - 4), ta có:
OB2 = 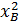 + +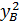 = (-3)2 + (-4)2 = (-3)2 + (-4)2
= 9 + 16 = 25
⇒ OB = 5 = R
Vậy B nằm trên đường tròn.
C(4,2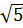 ), ta có: ), ta có:
OC2 = 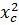 + +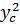 = 42 + ( 2 = 42 + ( 2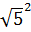 ) )
= 16 + 20 = 36 ⇒ OC = 6 > 5 ⇒ OC = R
Vậy C nằm ngoài đường tròn. |
|
Bài 3. Chứng minh rằng quỹ tích các điểm M sao cho 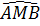 = 90°, trong đó AB là một đoạn thẳng cho trước, là đường tròn tâm O bán kính
= 90°, trong đó AB là một đoạn thẳng cho trước, là đường tròn tâm O bán kính  AB , với O là trung điểm AB.
Giải:
AB , với O là trung điểm AB.
Giải:
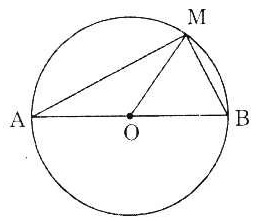
Giả sử M là điểm thỏa mãn 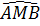 = 90°. = 90°.
Gọi O là trung điểm AB.
Khi đó, tam giác AMB vuông và MO là trung tuyến nên MO =  AB. Vậy M nằm AB. Vậy M nằm
trên dường tròn tâm O, bán kính  AB . AB .
Đảo lại, nếu N là điểm bất kì thuộc đường tròn tâm O, bán kính  AB, dĩ nhiên ta có: OA = OB = ON AB, dĩ nhiên ta có: OA = OB = ON
Khi đó, ta có tam giác ANB vuông tại N, nghĩa là điểm N thỏa mãn: 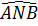 = 90°. = 90°.
|
 |
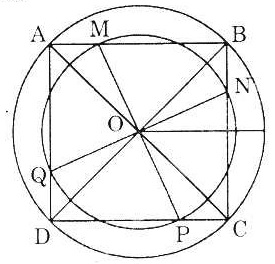
Bài 4. Cho hình vuông ABCD. Trên các cạnh AB, BC, CD, DA ta lần lượt lấy các điểm M, N, P, Q sao cho: AM = BN = CP = DQ. Gọi O là tâm hình vuông.
a) Chứng minh rằng N, O, Q thẳng hàng và M, O, P thẳng hàng.
b) Chứng minh bốn điểm M, N, P, Q cùng nằm trên một đường tròn.
c) Chứng minh ràng mọi điểm nằm trên đường tròn ở câu b đều nằm bên trong đường tròn đi qua bốn điểm A, B, C, D.
Giải:
a) Chứng minh  ONB - ONB -  OQD (c.g.c). OQD (c.g.c).
⇒ 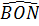 = = 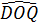 , do đó N, O, Q thẳng hàng. , do đó N, O, Q thẳng hàng.
Chứng minh tương tự ta có: M, O, P thẳng hàng.
b) Chứng minh OM = ON = OP = OQ (xét 4 tam giác bằng nhau).
Suy ra bốn điểm M, N, P, Q cùng nằm trên đường tròn tâm O. bán kính OM.
c) Đường tròn (ABCD) có tâm O, bán kính OA.
Ta có: 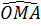 = = 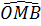 + + 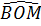 = 45° + = 45° + 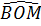 > 45o > 45o
Ta lại có: 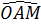 = 45°, do đó suy ra OA > OM. = 45°, do đó suy ra OA > OM.
Như vậy, mọi điểm của đường tròn qua (MNPQ) đều nằm bên trong đường tròn qua (ABCD). |
 |
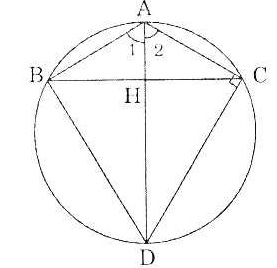
Bài 5. Cho  ABC cân tại A, đường cao AH = 1cm, HC = 4cm. Đường vuông góc với AC tại C cắt đường thẳng AH ở D. ABC cân tại A, đường cao AH = 1cm, HC = 4cm. Đường vuông góc với AC tại C cắt đường thẳng AH ở D.
a) Chứng minh rằng các điểm B, C thuộc đường tròn đường kính AD.
b) Tính độ dài AD. |
 |
Giải:
a) Xét hai tam giác  ADC và
ADC và  ADB
Ta có: AD chung
ADB
Ta có: AD chung
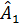 =
= 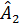 (Vì
(Vì  ABC cân nên AM là phân giác)
AC = AB (vì
ABC cân nên AM là phân giác)
AC = AB (vì  ABC cân tại A)
⇒
ABC cân tại A)
⇒  ADC =
ADC =  ADB ⇒
ADB ⇒ 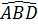 =
= 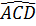 = 90°
⇔ B, C thuộc đường tròn đường kính AD.
b) Trong
= 90°
⇔ B, C thuộc đường tròn đường kính AD.
b) Trong  ABD vuông tại D, ta có:
AH.AD = AB2 = AH2+ BH2 ⇔ AD =
ABD vuông tại D, ta có:
AH.AD = AB2 = AH2+ BH2 ⇔ AD = 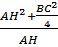 = 5cm
Vậy ta được AD = 5cm.
= 5cm
Vậy ta được AD = 5cm.
Bài 6. Cho  ABC, các đường cao BD và CE ABC, các đường cao BD và CE
a) Chứng minh rằng bốn điểm B, C, D, K nằm trên cùng một đường tròn.
b) Chứng minh rằng: DE < BC. |
|
Giải:
a) Ta có thể lựa chọn một trong hai cách trình bày sau:
Cách 1: Từ giả thiết, ta có: BD ⊥ AC ⇔ 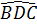 = 90°
⇒ D thuộc đường tròn có đường kính BC.
CE ⊥ AB ⇔
= 90°
⇒ D thuộc đường tròn có đường kính BC.
CE ⊥ AB ⇔ 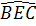 = 90°
⇒ E thuộc đường tròn có đường kính BC.
Vậy bốn điểm B, C, D, E thuộc đường tròn có đường kính BC.
Cách 2: Gọi O là trung điểm của BC, ta có:
-
= 90°
⇒ E thuộc đường tròn có đường kính BC.
Vậy bốn điểm B, C, D, E thuộc đường tròn có đường kính BC.
Cách 2: Gọi O là trung điểm của BC, ta có:
-  BEC vuông tại E và có EO là trung tuyến, nên:
OE = OD = OC. (1)
- ABCD vuông tại D và có DO là trung tuyến, nên:
OD = OB = OC. (2)
Từ (1) và (2), suy ra: OB = OE = OD - OC
Vậy B, C, D, E thuộc đường tròn (O; OB).
b) Trong đường tròn (O), ta có BC là đường kính của dường tròn, DE là dây (khác đường kính) nên DE < BC (đường kính là dây lớn nhất của đường tròn).
Bài 7. Cho
BEC vuông tại E và có EO là trung tuyến, nên:
OE = OD = OC. (1)
- ABCD vuông tại D và có DO là trung tuyến, nên:
OD = OB = OC. (2)
Từ (1) và (2), suy ra: OB = OE = OD - OC
Vậy B, C, D, E thuộc đường tròn (O; OB).
b) Trong đường tròn (O), ta có BC là đường kính của dường tròn, DE là dây (khác đường kính) nên DE < BC (đường kính là dây lớn nhất của đường tròn).
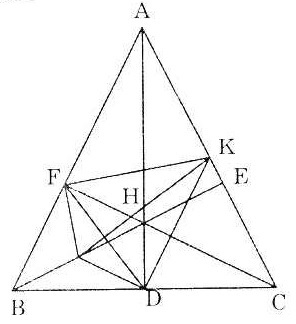
Bài 7. Cho  ABC cân tại A có các đường cao AD, BE, CF cắt nhau tại H.
a) Chứng minh bốn điểm B, D, H, F cùng thuộc một đường tròn. Xác định tâm I của đường tròn này.
b) Chứng minh bốn điểm A, F, D, C cùng thuộc một đường tròn. Xác định tâm K của đường tròn này.
c) Chứng minh IK đi qua trung điểm của FD.
d) Chứng minh B nằm ngoài đường tròn (K) đã nêu ở câu b.
Giải:
ABC cân tại A có các đường cao AD, BE, CF cắt nhau tại H.
a) Chứng minh bốn điểm B, D, H, F cùng thuộc một đường tròn. Xác định tâm I của đường tròn này.
b) Chứng minh bốn điểm A, F, D, C cùng thuộc một đường tròn. Xác định tâm K của đường tròn này.
c) Chứng minh IK đi qua trung điểm của FD.
d) Chứng minh B nằm ngoài đường tròn (K) đã nêu ở câu b.
Giải:
Gọi I là trung điểm BH, K là trung điểm AC.
a) ABFH vuông tại F có FI là trung tuyến:
⇒ FI =  BH BH
Tương tự: DI =  BH BH
⇒ FI = DI = IB = IH (= BH) BH)
⇒ Bốn điểm B, D, H, F cùng thuộc đường tròn tâm 1 bán kính .
b) Chứng minh tương tự ta cũng có bốn điểm A, F, D, C thuộc đường tròn (K) bán kính 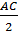 . .
|
 |
c) Từ chứng minh trên, ta có:
IF = ID ⇒ I = trung trực FD
KF = KD ⇒ K 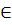 trung trực FD
⇒ IK là trung trực FD
⇒ IK đi qua trung điểm FD.
d) Do K là trung điểm AC nên tia BK nam giữa 2 tia BA và BC.
⇒
trung trực FD
⇒ IK là trung trực FD
⇒ IK đi qua trung điểm FD.
d) Do K là trung điểm AC nên tia BK nam giữa 2 tia BA và BC.
⇒ 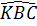 <
< 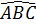 mà
mà 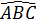 =
= 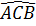 ⇒
⇒ 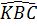 <
< 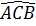 Xét
Xét  CKD có:
CKD có: 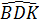 >
> 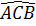 ( góc ngoài tam giác)
nên
( góc ngoài tam giác)
nên 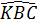 <
< 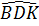 ⇒ BK > KD
B nằm ngoài đường tròn (K) bán kính
⇒ BK > KD
B nằm ngoài đường tròn (K) bán kính 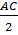 .
.
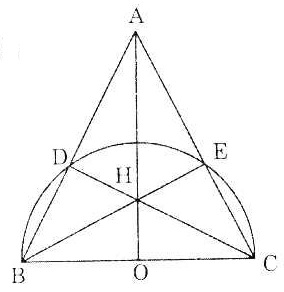
Bài 8. Cho  ABC có ba góc nhọn. Vẽ đường tròn đường kính BC cắt các cạnh AB và AC lần lượt tại D và E; BE và CD cắt nhau tại H. Chứng minh đường thẳng AH vuông góc với BC. ABC có ba góc nhọn. Vẽ đường tròn đường kính BC cắt các cạnh AB và AC lần lượt tại D và E; BE và CD cắt nhau tại H. Chứng minh đường thẳng AH vuông góc với BC. |
 |
Giải:
Ta có: BC là đường kính (O) và E 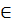 (O) (g)
⇒
(O) (g)
⇒ 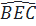 = 90o
⇒ BE là đường cao
= 90o
⇒ BE là đường cao  ABC
Tương tự: CD là đường cao
ABC
Tương tự: CD là đường cao  ABC
Do đó H là trực tâm
ABC
Do đó H là trực tâm  ABC
⇒ Đường thẳng AH ⊥ BC
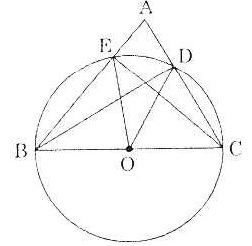
Bài 9. Cho đường tròn (O, R) và hai bán kính OA, OB. Trên các bán kính OA, OB lần lượt lấy các điểm M và N sao cho OM = ON, và dây CD đi qua M và N (M nằm giữa C và N).
a) Chứng minh rằng: CM = DK.
b) Giả sử:
ABC
⇒ Đường thẳng AH ⊥ BC
Bài 9. Cho đường tròn (O, R) và hai bán kính OA, OB. Trên các bán kính OA, OB lần lượt lấy các điểm M và N sao cho OM = ON, và dây CD đi qua M và N (M nằm giữa C và N).
a) Chứng minh rằng: CM = DK.
b) Giả sử: 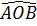 = 90o, hãy tính OM; ON theo R sao cho CM = MN = ND.
Giải:
a) Vẽ OI ⊥ CD, chứng minh I là trung điểm của CD và MN, từ đó suy ra: CM = DN.
= 90o, hãy tính OM; ON theo R sao cho CM = MN = ND.
Giải:
a) Vẽ OI ⊥ CD, chứng minh I là trung điểm của CD và MN, từ đó suy ra: CM = DN.
b) Nếu 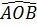 = 90° thì = 90° thì  IOM cân tại I. IOM cân tại I.
Đặt OI = x thì IM = x
Ta có: CM = MN = ND
⇒ IC = 3x
Áp dụng định lí Pitago, ta có:
x2 + (3x)2 = R, x2 = 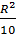
Áp dụng định lí Pitago vào tam giác vuông IOM ta được:
OM2 = OI2 + IM2 = 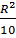 + + 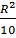 = = 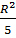
Vậy OM = 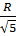 , ON = , ON = 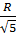 |
|
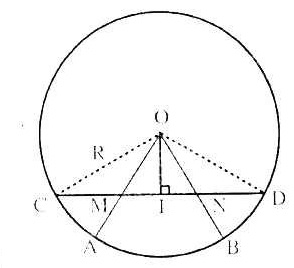
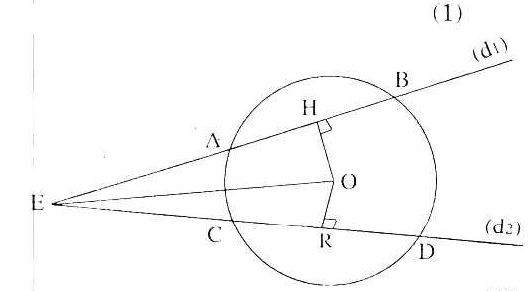
Bài 10. Từ một điểm E ở ngoài đường tròn (O) dựng hai đường thẳng (d1) cắt (O) lần lượt tại A và B, (d2) cắt (O) lần lượt tại C và D sao cho AB = CD. Dựng OA ⊥AB và OR ⊥ CD.
Chứng minh: a) EH = ER b) EA = EC
Giải:
a) Vì AB = CD nên OH = OR
Hai tam giác vuông OEH và ORH có:
- OB chung
- OH = OR nên  OEH =
OEH =  OKH
⇒ EH = ER (đpcm) (1)
b) OH ⊥ AB n là trung điểm của AB ⇒ AH =
OKH
⇒ EH = ER (đpcm) (1)
b) OH ⊥ AB n là trung điểm của AB ⇒ AH = 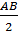 OR ⊥ CD ⇒ R là trung điểm của CD
⇒ RC =
OR ⊥ CD ⇒ R là trung điểm của CD
⇒ RC = 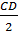 Nhưng: AB = CD nên HA = KC (2)
Lấy (1) trừ (2) vế theo vế, ta có:
EH - HA - EH – RC ⇒ EA = EC (đpcm)
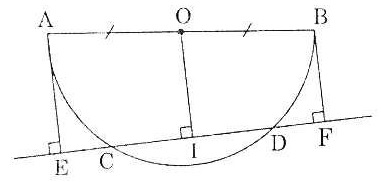
Bài 11. Cho một nửa đường tròn (O), đường kính AB và một dây cung CD. Kẻ AE và BF vuông góc với CD. Chứng minh rằng: CE = DF
Giải:
Nhưng: AB = CD nên HA = KC (2)
Lấy (1) trừ (2) vế theo vế, ta có:
EH - HA - EH – RC ⇒ EA = EC (đpcm)
Bài 11. Cho một nửa đường tròn (O), đường kính AB và một dây cung CD. Kẻ AE và BF vuông góc với CD. Chứng minh rằng: CE = DF
Giải:
Dựng OI ⊥ CD ⇒ IC = ID (1)
Ta có: AE // BF ⇒ ABFE là một hình thang.
Ta lại có O là trung điểm AB và OI song song với hai đáy hình thang ABFE nên I là trung điểm EF.
⇒ IE = IF (2)
Trừ (2) cho (1) vế theo vế, ta có:
IE - IC = IF - ID ⇔ CE = DF
Vậy: CE = DF |
 |
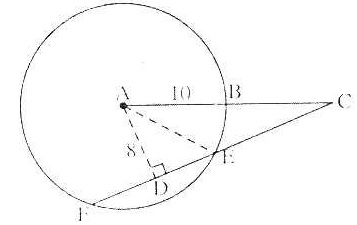
| Bài 12. Cho đường tròn tâm A bán kính AB. Dây FE kéo dài cắt đường thẳng AB tại C (E ở giữa F và C). Hạ AD ⊥ CF. Cho AB = 10cm; AD = 8cm; CF = 21cm. Tính CE và CA. |
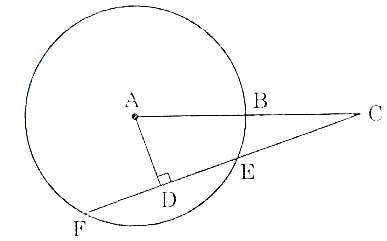 |
Giải:
Áp dụng định lí Pitago vào tam giác vuông ADE, ta tính được:
DE = 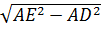 = = 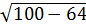 = 6 = 6
Suy ra CE = CF – 2DE = 21 – 12 = 9
Vậy CE = 9cm
CD = CE + ED = 9 + 6 = 15
Áp dụng định lí Pitago vào tam giác vuông ADC:
AC = 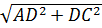 = = 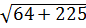 = = 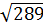 = 17 = 17
Suy ra CA = 17cm. |
|
Bài 13. Cho đường tròn (O) và hai dây AH và CD bằng nhau và cắt nhau tại điểm E. Chứng tỏ rằng điểm E chia các đoạn thẳng AB và CD thành các đoạn thẳng bằng nhau từng đôi một.
Giải:
Dựng OH ⊥ AB và OI ⊥ CD. Thế thì H là trung điểm của dây AB và I là trung điểm của dây CD (đường kính vuông góc với một dây).
Ta có: AB = CD (gt)
⇒ AH = HB = CI = ID
Đồng thời OH = OI (liên hệ giữa dây và khoảng cách đến tâm dây).
Hai tam giác vuông OHE và OIE bằng nhau vì có một cạnh góc vuông bằng nhau và cạnh huyền chung.
Suy ra: HE = IE
Ta có: AH + HE = DI + IE ⇒ AE = DE
Mặt khác: BE = AB - AE = CD - DE = CE. |
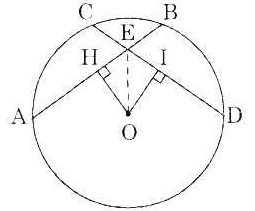 |
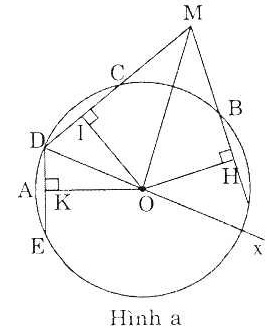
Bài 14. Cho đường tròn (O; R), các dây AB, CD, DE. Kẻ OH, OI, OK lần lượt vuông góc với AB, CD, DE tại H, I, K.
a) Chứng minh rằng nếu AB = CD thì OH = OI và ngược lại.
b) Chứng minh rằng nếu CD = DE thì tia Dx kẻ qua O là tia phân giác góc CDE.
c) Hai đường thẳng AB, DC cát nhau tại M. Giả sử B nằm giữa A và M; C nằm giữa D và M. Chứng minh rằng nếu MB = MC thì AB = CD và đảo lại.
d) Dựng hình bình hành có hai đỉnh là hai điểm A, B đã cho, hai đỉnh còn lại nằm trên (O; R).
Giải:
Ta có: HA = 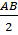 = = 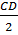 = ID = ID
Do đó:  OAH = OAH =  ODI ODI
Vậy OH = OI
Đảo lại với OH = OI,  OAH = OAH =  CDI và mệnh đề đảo cũng đúng (hình a) CDI và mệnh đề đảo cũng đúng (hình a)
b) Áp dụng câu a) ta có:
OK = OI
Vậy O ở trên đường phân giác của góc EDC, suy ra tia Dx kẻ qua O là tia phân giác góc 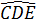 |
 |
c) Vì MB = MC và OB = R = OC nên OM là trung trực của BC mà  MBC cân đỉnh M nên OM cũng là phân giác góc DMA. MBC cân đỉnh M nên OM cũng là phân giác góc DMA.
Suy ra: OI = OH. Áp dụng phần đảo câu a) ta có:
AB = CD.
Đảo lại với AB = CD thì OI = OH
OM là phân giác góc 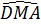 , ta có , ta có
 OMI = OMI =  OMH. OMH.
Suy ra MI = MH và MC = MI - CI = MH - BH = MB; hay MC = MB. |
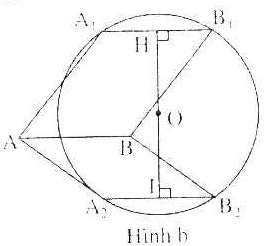 |
d) A, B là hai đỉnh kề nhau. Cần dựng dây A1B1, của (O) sao cho A1B1 song song và bằng AB.
Dựng một dây của (O) bằng AB, ta có khoảng cách từ dây đó với O bằng d chẳng hạn. Kẻ đường kính vuông góc với đường thẳng AB rồi lấy trên đó các điểm H, I sao cho OH = OI = d
Dựng các dây A1B1, A2B2 ⊥ HI tại H, I (hình b)
Theo câu a) A1B1 = AB = A2B2 . Hơn nữa chúng song song với AB (do cùng vuông góc với AH nên AA1B1B và AA2B2B là các đỉnh hình bình hành cần dựng).
Ngoài hai dây đó mọi dây song song với AB đều không bằng AB vì cách O một khoảng cách d. Vậy trường hợp này có hai nghiệm hình.
* A, B là hai đỉnh đối nhau, hai đỉnh kia phải là một dây nhận trung điểm K của AB làm trung điểm. Ta chỉ việc dựng dây CD ⊥ OK tại K. Với K trùng O thì có vô số nghiệm hình; Với OK < R, thì có một nghiệm hình. Với OK 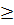 R, không có nghiệm hình.
R, không có nghiệm hình.
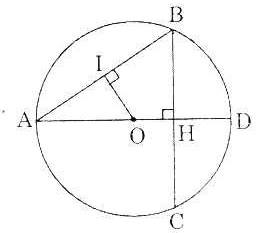
| Bài 15. Cho đường tròn tâm O đường kính AD, dây cung AB. Qua B kẻ đường vuông góc với AD cắt đường tròn ở C. Tính bán kính của đường tròn nếu biết AB = 10cm và BC = 12cm. |
 |
Giải:
Gọi H là giao điểm của BC với AD thì:
HB = HC =  BC = 6(cm)
Kẻ OI ⊥ AB, ta có IA – IB -
BC = 6(cm)
Kẻ OI ⊥ AB, ta có IA – IB -  AB = 5 (cm)
Trong tam giác vuông AHB, theo định lí Pitago:
Ta có: AH2 + HB2 = AB2
hay AH2 = 102 – 62 = 64 ⇒ AH = 8 (cm)
AB = 5 (cm)
Trong tam giác vuông AHB, theo định lí Pitago:
Ta có: AH2 + HB2 = AB2
hay AH2 = 102 – 62 = 64 ⇒ AH = 8 (cm)
 AIO
AIO 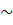
 AHB nên:
AHB nên:
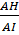 =
= 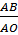 ⇒ AO =
⇒ AO = 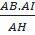 =
= 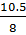 = 6,25 (cm)
Vậy bán kính đường tròn tâm O là R = 6,25 cm.
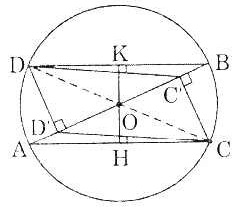
Bài 16. Cho đường tròn tâm O, đường kính AB. Từ A và B kẻ hai dây cung AC và BD song song với nhau.
a) So sánh AC và BD.
b) Chứng minh ha điểm C, O, D thẳng hàng.
c) Kẻ CC’ và DD’ vuông góc với AB. Chứng minh tứ giác CC’DD’ là hình bình hành.
Giải:
a) Vì AC // BD nên từ O kẻ OH vuông góc với AC thì OH ⊥ BD tại K.
Khi đó
= 6,25 (cm)
Vậy bán kính đường tròn tâm O là R = 6,25 cm.
Bài 16. Cho đường tròn tâm O, đường kính AB. Từ A và B kẻ hai dây cung AC và BD song song với nhau.
a) So sánh AC và BD.
b) Chứng minh ha điểm C, O, D thẳng hàng.
c) Kẻ CC’ và DD’ vuông góc với AB. Chứng minh tứ giác CC’DD’ là hình bình hành.
Giải:
a) Vì AC // BD nên từ O kẻ OH vuông góc với AC thì OH ⊥ BD tại K.
Khi đó  OHA và
OHA và  OKB bằng nhau.
Do đó HA = KB ⇒ AC = BD
b)
OKB bằng nhau.
Do đó HA = KB ⇒ AC = BD
b)  OHC =
OHC =  OKD ⇒
OKD ⇒ 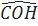 =
= 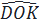 . Mà ba điểm A, O, B thẳng hàng, còn hai tia OC và OD trên hai nửa mặt phẳng đối nhau qua bờ là AB. Nên C, O, D thẳng hàng.
. Mà ba điểm A, O, B thẳng hàng, còn hai tia OC và OD trên hai nửa mặt phẳng đối nhau qua bờ là AB. Nên C, O, D thẳng hàng.
c) Kẻ DD’ và CC’ vuông góc với AB. Dễ thấy các tam giác DD’O và CC’O bằng nhau. ⇒ DD’ = CC’.
⇒ Tứ giác CC’DD’ là hình bình hành. |
 |
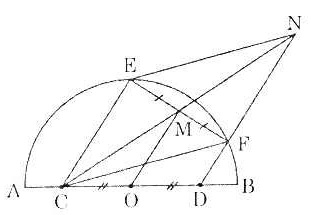
Bài 17. Cho nửa đường tròn tâm O đường kính AB, trên đoạn AB lấy hai điểm C và D sao cho OC = OD. Từ C và D vẽ hai tia song song với nhau và lần lượt cắt nửa đường tròn tại E và F. Gọi M là trung điểm của dây EF, gọi N là giao điểm của hai tia CM và DF. Chứng minh rằng:
a) Tứ giác CENF là hình bình hành.
b) OM // CE
c) CE và DF vuông góc với EF. |
 |
Giải:
a) CENF là hình bình hành:
Xét hai tam giác MCE và MNF có:
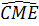 =
= 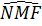 (đối đỉnh)
ME = MF (gt) (1)
(đối đỉnh)
ME = MF (gt) (1)
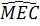 =
= 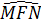 (so le trong)
⇒
(so le trong)
⇒  MCE =
MCE =  MNF (g.c.g) ⇒ MC- MN (2)
Từ (1) và (2) suy ra: CKNF là hình bình hành.
b) OM // CE:
Xét
MNF (g.c.g) ⇒ MC- MN (2)
Từ (1) và (2) suy ra: CKNF là hình bình hành.
b) OM // CE:
Xét  CDN có: OC = OD (gt) và MC = MN (cmt)
⇒ OM là đường trung bình của
CDN có: OC = OD (gt) và MC = MN (cmt)
⇒ OM là đường trung bình của  CDN
⇒ OM // DN mà DN // CE (gt) ⇒ OM // CE (đpcm).
c) CE và DF vuông góc với EF:
Ta có đường kính OM đi qua trung điểm M của EF. ⇒ OM ⊥ EF
Từ kết qua câu b) ⇒ CE và DF vuông góc với HF.
CDN
⇒ OM // DN mà DN // CE (gt) ⇒ OM // CE (đpcm).
c) CE và DF vuông góc với EF:
Ta có đường kính OM đi qua trung điểm M của EF. ⇒ OM ⊥ EF
Từ kết qua câu b) ⇒ CE và DF vuông góc với HF.
© Bản quyền thuộc về
Bài kiểm tra. Ghi rõ nguồn Bài kiểm tra.com khi sao chép nội dung này.