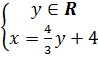Giải bài tập Toán 9, chương III, bài 1: Phương trình bậc nhất hai ẩn.
2019-08-22T04:02:07-04:00
2019-08-22T04:02:07-04:00
Giải bài tập Toán 9, chương III, bài 1: Phương trình bậc nhất hai ẩn: Tóm tắt kiến thức, ví dụ, hướng dẫn giải bài tập trong sách giáo khoa và bài tập luyện thêm.
/themes/cafe/images/no_image.gif
Bài Kiểm Tra
https://baikiemtra.com/uploads/bai-kiem-tra-logo.png
Thứ ba - 20/08/2019 22:19
Giải bài tập Toán 9, chương III, bài 1: Phương trình bậc nhất hai ẩn: Tóm tắt kiến thức, ví dụ, hướng dẫn giải bài tập trong sách giáo khoa và bài tập luyện thêm.
A. Tóm tắt kiến thức
1. Khái niệm về phương trình bậc nhất hai ẩn
Phương trình bậc nhất hai ẩn x, y là một hệ thức dạng: ax + by = c (1)
trong đó a, b, c là những số đã biết, a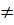 0 hoặc b
0 hoặc b 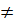 0.
Các số a, b, c được gọi lừ các hệ số của phương trình này.
Nghiệm của phương trình (1) là một cặp số(x0 ; y0) sao cho: ax0 + by0 = c.
Lưu ý. a) Khi (x0 ; y0) là một nghiệm của phương trình (1) ta cũng nói rằng cặp số này thỏa mãn phương trình (1).
b) Mỗi nghiệm (x0 ; y0) của phương trình (1) được biểu diễn trên mặt phẳng toạ độ bởi một điếm có toạ độ là (x0 ; y0).
c) Muốn tìm một nghiệm của phương trình ax + by = c, ta có thể làm như sau :
- Nếu a
0.
Các số a, b, c được gọi lừ các hệ số của phương trình này.
Nghiệm của phương trình (1) là một cặp số(x0 ; y0) sao cho: ax0 + by0 = c.
Lưu ý. a) Khi (x0 ; y0) là một nghiệm của phương trình (1) ta cũng nói rằng cặp số này thỏa mãn phương trình (1).
b) Mỗi nghiệm (x0 ; y0) của phương trình (1) được biểu diễn trên mặt phẳng toạ độ bởi một điếm có toạ độ là (x0 ; y0).
c) Muốn tìm một nghiệm của phương trình ax + by = c, ta có thể làm như sau :
- Nếu a 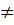 0 thì ta thay y bởi một giá trị y0 rồi từ ax + by0 = c suy ra giá trị tương ứng x0 của x. Cặp giá trị tương ứng (x0 ; y0) là một nghiệm của phương trình.
- Nếu b
0 thì ta thay y bởi một giá trị y0 rồi từ ax + by0 = c suy ra giá trị tương ứng x0 của x. Cặp giá trị tương ứng (x0 ; y0) là một nghiệm của phương trình.
- Nếu b 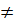 0 thì ta thay x bởi một giá trị x0 rồi từ ax0 + by = c suy ra giá trị tương ứng y0 của y. Cặp giá trị tương ứng (x0 ; y0) là một nghiệm của phương trình.
2. Tập nghiệm của phương trình bậc nhất hai ẩn
Nếu a
0 thì ta thay x bởi một giá trị x0 rồi từ ax0 + by = c suy ra giá trị tương ứng y0 của y. Cặp giá trị tương ứng (x0 ; y0) là một nghiệm của phương trình.
2. Tập nghiệm của phương trình bậc nhất hai ẩn
Nếu a 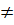 0 và b
0 và b 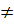 0 thì với mỗi x
0 thì với mỗi x 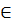 R, từ ax + by = c ta suy ra một giá trị tương ứng y = -
R, từ ax + by = c ta suy ra một giá trị tương ứng y = -  x +
x +  Như vậy, phương trình có vô số nghiệm có dạng
Như vậy, phương trình có vô số nghiệm có dạng 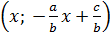 hay
hay 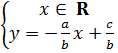 Ta gọi đó là công thức nghiệm tổng quát của phương trình.
Tương tự, với mỗi y
Ta gọi đó là công thức nghiệm tổng quát của phương trình.
Tương tự, với mỗi y 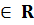 , ta cũng suy ra x =
, ta cũng suy ra x = 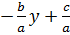 ; và cũng có nghiệm tổng quát là:
; và cũng có nghiệm tổng quát là:
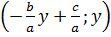 hay
hay 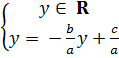 Tập nghiệm của phương trình ax + by = c được biểu diễn bởi đồ thị của hàm số bậc nhất
y = -
Tập nghiệm của phương trình ax + by = c được biểu diễn bởi đồ thị của hàm số bậc nhất
y = - 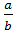 x +
x +  Đó là một đường thẳng cắt cả hai trục toạ độ.
+ Nếu a = 0 thì với mỗi A
Đó là một đường thẳng cắt cả hai trục toạ độ.
+ Nếu a = 0 thì với mỗi A 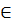 R ta đều có y =
R ta đều có y =  Nghiệm tổng quát của phương trình là
Nghiệm tổng quát của phương trình là 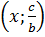 ; hay
; hay 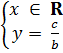 Tập nghiệm của phương trình là đường thẳng vuông góc với Oy và cắt Oy tại điểm có tung độ là
Tập nghiệm của phương trình là đường thẳng vuông góc với Oy và cắt Oy tại điểm có tung độ là  + Nếu b = 0 thì với mỗi y
+ Nếu b = 0 thì với mỗi y 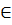 R ta đều có x =
R ta đều có x =  .
Nghiệm tổng quát của phương trình là
.
Nghiệm tổng quát của phương trình là 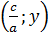 hay
hay 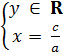 Tập nghiệm của phương trình là đường thẳng vuông góc với trục Ox và cắt Ox tại điểm có hoành độ là:
Tập nghiệm của phương trình là đường thẳng vuông góc với trục Ox và cắt Ox tại điểm có hoành độ là:  Tổng quát : Tập nghiệm của một phương trình ax + by = c được biểu diễn bởi một đường thẳng. Đường thẳng này được gọi là đường thẳng ax + by = c.
Lưu ý. Muốn vẽ dường thẳng ax + by = c, ta có thể làm như sau :
- Nếu a
Tổng quát : Tập nghiệm của một phương trình ax + by = c được biểu diễn bởi một đường thẳng. Đường thẳng này được gọi là đường thẳng ax + by = c.
Lưu ý. Muốn vẽ dường thẳng ax + by = c, ta có thể làm như sau :
- Nếu a 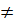 0, ta cho A hai giá trị phân biệt x1, x2, tính các giá trị tương ứng y1,y2 ; xác định hai điểm A(x1 ; y1), B(x2 ; y2), rồi kẻ đường thẳng AB.
- Nếu b
0, ta cho A hai giá trị phân biệt x1, x2, tính các giá trị tương ứng y1,y2 ; xác định hai điểm A(x1 ; y1), B(x2 ; y2), rồi kẻ đường thẳng AB.
- Nếu b 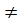 0, ta cho y hai giá trị phân biệt y1,y2, tính các giá trị tương ứng x1,x2 ; xác định hai điểm A(x1 ; y1), B(x2 ; y2), rồi kẻ đường thẳng AB.
B. Ví dụ
Ví dụ 1. Hãy cho biết những phương trình nào sau đây là phương trình bậc nhất hai ẩn và chỉ rõ hai ẩn :
3x - 5y = 7 ; 4u + 7v = - 5 ; 6s - 2t = 0 ; x2 - 4y = 1.
Giải: Phương trình 3x - 5y = 7 là một phương trình bậc nhất của hai ẩn x và y. Phương trình 4u + 7v = -5 là một phương trình bậc nhất của hai ẩn u và v.
Phương trình 6s - 2t = 0 là một phương trình bậc nhất của hai ẩn s và t.
Phương trình x2 - 4y = 1 không phải là một phương trình bậc nhất hai ẩn vì bậc của x là 2.
Ví dụ 2. Hãy chỉ rõ các hệ số a, b, c của mỗi phương trình bậc nhất hai ẩn sau :
2x + 7y = 5 ; 0x + 5y = -4 ; 3s - 0t = 2 ; 6u - 5v = 0.
Giải: Phương trình 2x + 7y - 5 có các hệ số a = 2, b = 7, c = 5.
Phương trình 0x + 5y = -4 có các hệ số : a = 0, b = 5 ; c - -4.
Phương trình 3s - 0t = 2 có các hệ số: a = 3, b = 0 ; c = 2.
Phương trình 6u - 5v = 0 có các hệ số : a = 6, b = -5, c = 0.
Ví dụ 3. Cho phương trình 4x - 3y - 6. Xét xem những cặp số nào sau đây là nghiệm của nó ?
(3 ; 2); (-6 ; -10); (5 ; -1);
0, ta cho y hai giá trị phân biệt y1,y2, tính các giá trị tương ứng x1,x2 ; xác định hai điểm A(x1 ; y1), B(x2 ; y2), rồi kẻ đường thẳng AB.
B. Ví dụ
Ví dụ 1. Hãy cho biết những phương trình nào sau đây là phương trình bậc nhất hai ẩn và chỉ rõ hai ẩn :
3x - 5y = 7 ; 4u + 7v = - 5 ; 6s - 2t = 0 ; x2 - 4y = 1.
Giải: Phương trình 3x - 5y = 7 là một phương trình bậc nhất của hai ẩn x và y. Phương trình 4u + 7v = -5 là một phương trình bậc nhất của hai ẩn u và v.
Phương trình 6s - 2t = 0 là một phương trình bậc nhất của hai ẩn s và t.
Phương trình x2 - 4y = 1 không phải là một phương trình bậc nhất hai ẩn vì bậc của x là 2.
Ví dụ 2. Hãy chỉ rõ các hệ số a, b, c của mỗi phương trình bậc nhất hai ẩn sau :
2x + 7y = 5 ; 0x + 5y = -4 ; 3s - 0t = 2 ; 6u - 5v = 0.
Giải: Phương trình 2x + 7y - 5 có các hệ số a = 2, b = 7, c = 5.
Phương trình 0x + 5y = -4 có các hệ số : a = 0, b = 5 ; c - -4.
Phương trình 3s - 0t = 2 có các hệ số: a = 3, b = 0 ; c = 2.
Phương trình 6u - 5v = 0 có các hệ số : a = 6, b = -5, c = 0.
Ví dụ 3. Cho phương trình 4x - 3y - 6. Xét xem những cặp số nào sau đây là nghiệm của nó ?
(3 ; 2); (-6 ; -10); (5 ; -1); 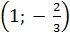 ; (-1 ; 4).
Phân tích. Muốn biết (3 ; 2) có phải là một nghiệm của phương trình đã cho hay không, ta thay x = 3 ; y = 2 vào phương trình rồi xét xem giá trị hai vế của phương trình có bằng nhau hay không.
Giải. Với cặp số (3 ; 2), thay x = 3, y = 2 vào phương trình đã cho thì vế trái có giá trị là :
4.3 - 3.2 = 12 - 6 = 6.
Do đó hai vế có cùng giá trị.
Vậy cặp số (3 ; 2) là một nghiệm của phương trình.
Với cặp số (-6; -10), vế trái của phương trình đã cho có giá trị là :
4.(-6) - 3.(-10) = -24 + 30 = 6.
Do đó hai vế có cùng giá trị.
Vậy cặp số (-6 ; -10) là một nghiệm của phương trình.
Với cặp số (5 ; -1), vế trái của phương trình đã cho có giá trị là : 4.5 - 3.(-1) = 20 + 3 = 23.
Vì vế phải của phương trình là 6 nên hai vế có giá trị khác nhau.
Vậy cặp số (5 ; -1) không phải là một nghiệm của phương trình.
Với cặp số
; (-1 ; 4).
Phân tích. Muốn biết (3 ; 2) có phải là một nghiệm của phương trình đã cho hay không, ta thay x = 3 ; y = 2 vào phương trình rồi xét xem giá trị hai vế của phương trình có bằng nhau hay không.
Giải. Với cặp số (3 ; 2), thay x = 3, y = 2 vào phương trình đã cho thì vế trái có giá trị là :
4.3 - 3.2 = 12 - 6 = 6.
Do đó hai vế có cùng giá trị.
Vậy cặp số (3 ; 2) là một nghiệm của phương trình.
Với cặp số (-6; -10), vế trái của phương trình đã cho có giá trị là :
4.(-6) - 3.(-10) = -24 + 30 = 6.
Do đó hai vế có cùng giá trị.
Vậy cặp số (-6 ; -10) là một nghiệm của phương trình.
Với cặp số (5 ; -1), vế trái của phương trình đã cho có giá trị là : 4.5 - 3.(-1) = 20 + 3 = 23.
Vì vế phải của phương trình là 6 nên hai vế có giá trị khác nhau.
Vậy cặp số (5 ; -1) không phải là một nghiệm của phương trình.
Với cặp số 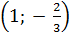 vế trái của phương trình đã cho có giá trị là :
4.1 -3.
vế trái của phương trình đã cho có giá trị là :
4.1 -3.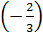 = 4 + 2 = 6.
Do đó hai vế có cùng giá trị.
Vậy cặp số
= 4 + 2 = 6.
Do đó hai vế có cùng giá trị.
Vậy cặp số 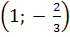 là một nghiệm của phương trình.
Với cặp số (-1 ; 4), vế trái của phương trình đã cho có giá trị là : 4.(-1) - 3.(4) = -4 - 12 = -16.
Vì vế phải của phương trình là 6 nên hai vế có giá trị khác nhau.
Vậy cặp số (-1 ; 4) không phải là một nghiệm của phương trình.
Ví dụ 4. Viết nghiệm tổng quát của mỗi phương trình sau :
a) 7x - 5y = 11 ;
b) 4x - 0y = 19 ;
c) 0x + 5y = 20.
Giải: a) Vì a = 7, b = -5 nên với mỗi x
là một nghiệm của phương trình.
Với cặp số (-1 ; 4), vế trái của phương trình đã cho có giá trị là : 4.(-1) - 3.(4) = -4 - 12 = -16.
Vì vế phải của phương trình là 6 nên hai vế có giá trị khác nhau.
Vậy cặp số (-1 ; 4) không phải là một nghiệm của phương trình.
Ví dụ 4. Viết nghiệm tổng quát của mỗi phương trình sau :
a) 7x - 5y = 11 ;
b) 4x - 0y = 19 ;
c) 0x + 5y = 20.
Giải: a) Vì a = 7, b = -5 nên với mỗi x 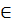 R, từ 7x - 5y = 11 ta suy ra:
-5y = -7x + 11 hay y =
R, từ 7x - 5y = 11 ta suy ra:
-5y = -7x + 11 hay y =  x -
x - 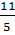 .
Vậy nghiệm tổng quát của phương trình là:
.
Vậy nghiệm tổng quát của phương trình là:
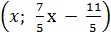 hay
hay 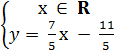 (Nếu ta lấy một giá trị tuỳ ý y
(Nếu ta lấy một giá trị tuỳ ý y 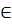 R thì từ 7x - 5y = 11 suy ra
7x = 5y + 11 hay x =
R thì từ 7x - 5y = 11 suy ra
7x = 5y + 11 hay x =  y +
y + 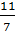 .
và có nghiệm tổng quát là
.
và có nghiệm tổng quát là 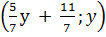 hay
hay 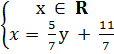 b) Với mỗi giá trị y
b) Với mỗi giá trị y 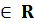 , từ 4x - 0y = 19, ta đều có x =
, từ 4x - 0y = 19, ta đều có x = 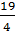 .
Vậy nghiệm tổng quát của phương trình là
.
Vậy nghiệm tổng quát của phương trình là 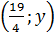 ; hay
; hay 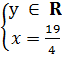 c) Với mỗi giá trị x
c) Với mỗi giá trị x 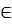 R, từ 0x + 5y = 20 suy ra y = 4.
Vậy nghiệm tổng quát của phương trình là (x ; 4) hay
R, từ 0x + 5y = 20 suy ra y = 4.
Vậy nghiệm tổng quát của phương trình là (x ; 4) hay 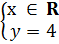 Ví dụ 5. Biểu diễn tập nghiệm của phương trình 3x + 2y = 6 trên một mặt phẳng toạ độ.
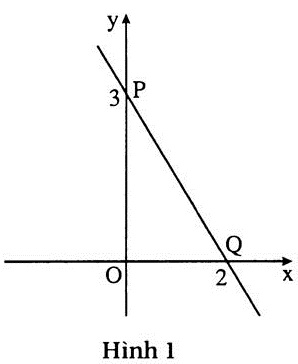
Ví dụ 5. Biểu diễn tập nghiệm của phương trình 3x + 2y = 6 trên một mặt phẳng toạ độ.
Giải. (h. 1) Từ 3x + 2y = 6 suy ra y = -  x + 3. x + 3.
Tập nghiệm của phương trình được biểu diễn bởi đồ thị của hàm số y = -  x + 3. Cho x = 0, ta có y = - x + 3. Cho x = 0, ta có y = -  .0 + 3 = 3. Chọn điểm P(0 ; 3). .0 + 3 = 3. Chọn điểm P(0 ; 3).
Cho y = 0, ta có 0 = -  x + 3. Suy ra x = 2. x + 3. Suy ra x = 2.
Chọn điểm Q(2 ; 0). Kẻ đường thẳng PQ. |
 |
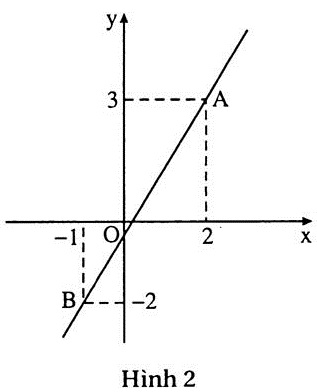
Ví dụ 6. Biểu diễn tập nghiệm của phương trình 5x - 3y = 1 trên một mặt phẳng toạ độ.
Phân tích. Nếu dùng cách giải như ví dụ 5 thì ta phải vẽ đường thẳng
y =  x - x -  . Khi đó các điểm P . Khi đó các điểm P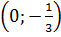 , Q , Q 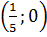 đều là nghiệm của phương trình. Nhưng việc xác định p và Q không thuận lợi. Để vẽ đường thẳng này ta chọn hai điểm khác có toạ độ là những số nguyên. đều là nghiệm của phương trình. Nhưng việc xác định p và Q không thuận lợi. Để vẽ đường thẳng này ta chọn hai điểm khác có toạ độ là những số nguyên.
Giải: (h.2) Thay x = 2, ta có 5.2 - 3y = 1.
Suy ra 3y = 9. Do đó y = 3.
Chọn điểm A(2 ; 3).
Thay x = - l, ta có5.(-1) -3y= 1 hay -5 - 3y = 1.
Suy ra y = -2.
Chọn điểm B(-1 ; -2).
Vẽ đường thẳng AB. |
 |
Ví dụ 7. Biểu diễn tập nghiệm của phương trình 0x + 2y = -4 trên một mặt phẳng toạ độ.
❖ Phân tích. Với mọi x 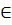 R, từ 0x + 2y = -4 suy ra y = -2. Như vậy mọi cặp số (x ; -2) đều là nghiệm của phương trình. Mọi điểm có toạ độ (x ; -2) nằm phía dưới trục Ox và cách trục Ox một khoảng là 2 đơn vị. Vì thế chúng tạo nên một đường thẳng song song với trục Ox và đi qua điểm (0 ; -2).
R, từ 0x + 2y = -4 suy ra y = -2. Như vậy mọi cặp số (x ; -2) đều là nghiệm của phương trình. Mọi điểm có toạ độ (x ; -2) nằm phía dưới trục Ox và cách trục Ox một khoảng là 2 đơn vị. Vì thế chúng tạo nên một đường thẳng song song với trục Ox và đi qua điểm (0 ; -2).
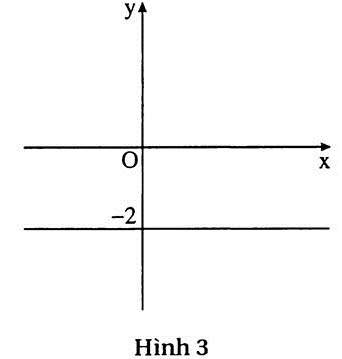
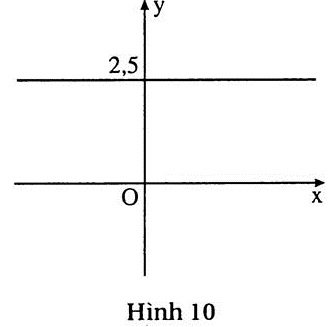
Giải: (h.3) Từ 0x + 2y = - 4 suy ra y = - 2.
Vậy tập nghiệm của phương trình đã cho là đường thẳng song song với Ox và cắt Oy tại điểm (0; -2). |
 |
Ví dụ 8. Biểu diễn tập nghiệm của phương trình 3x - 0y = 9 trên một mặt phẳng toạ độ.
❖ Phân tích. Với mọi y 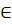 R, từ 3x - 0y = 9 suy ra x = 3. Như vậy mọi cặp số (3 ; y) đều là nghiệm của phương trình. Mọi điểm có toạ độ (3 ; y) đều nằm bên phải trục Oy và cách trục Oy một khoảng là 3 đơn vị. Vì thế chúng tạo nên một đường thẳng song song với trục Oy và đi qua điểm (3 ; 0).
R, từ 3x - 0y = 9 suy ra x = 3. Như vậy mọi cặp số (3 ; y) đều là nghiệm của phương trình. Mọi điểm có toạ độ (3 ; y) đều nằm bên phải trục Oy và cách trục Oy một khoảng là 3 đơn vị. Vì thế chúng tạo nên một đường thẳng song song với trục Oy và đi qua điểm (3 ; 0).
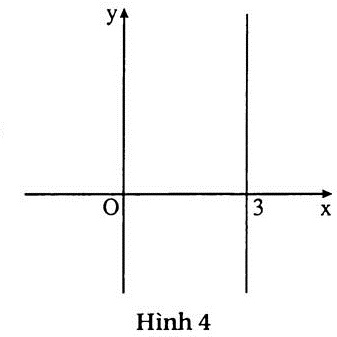
Giải: (h.4) Từ 3x - 0y = 9 suy ra x = 3.
Vậy tập nghiệm của phương trình đã cho là đường thẳng song song với Oy và cắt Ox tại điểm (3 ; 0). |
 |
C. Hướng dẫn giải bài tập trong sách giáo khoa
1. Hướng dẫn : Thay (x ; y) bởi (-2 ; 1) vào mỗi phương trình rồi so sánh giá trị hai vế của mỗi phương trình. Tương tự đối với các cặp số còn lại.
Trả lời : a) (0 ; 2), (4 ; -3) là nghiệm ; b) (-1 ; 0), (4 ; -3) là nghiệm.
2. Giải.
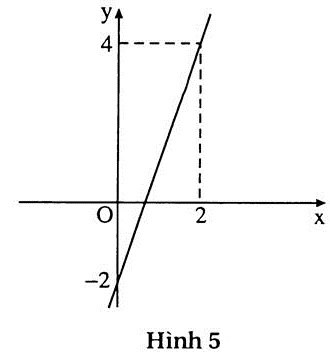
a) (h.5) Nghiệm tổng quát :
(x; 3x - 2) hay 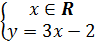
|
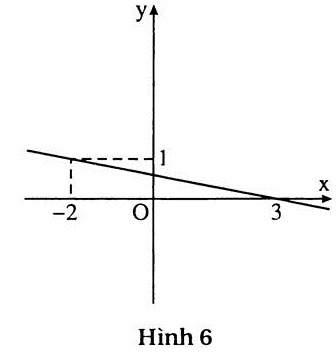
b) (h.6) Nghiệm tổng quát :
(3 – 5y; y) hay 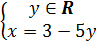
|
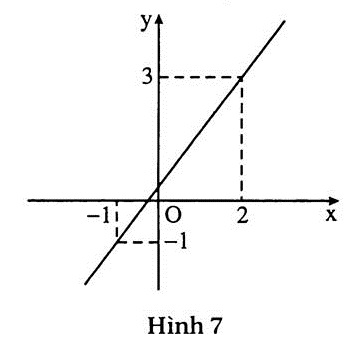
c) (h.7) Nghiệm tổng quát :
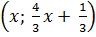 hay hay 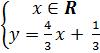
|
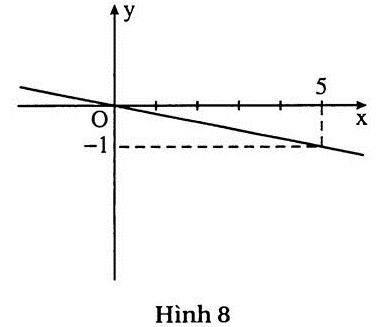
d) (h.8) Nghiệm tổng quát :
(-5y; y) hay 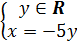
|
e) (h.9) Nghiệm tổng quát :
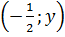 hay hay 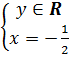
|
f) Nghiệm tổng quát :
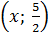 hay hay 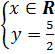
|
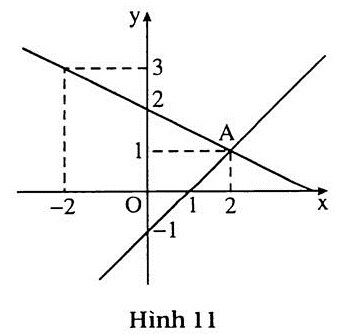
3. Giải (h. 11).
Toạ độ giao điểm của hai đường thẳng là A(2; 1).
Thử lại ta thấy cặp số này là nghiệm của cả hai phương trình đã cho. |
 |
D. Bài tập luyện thêm
1. Với mỗi phương trình sau hãy tìm một nghiệm của nó :
5x + 2y = 7 ; b) 3x - 0y = -9 ; c) 0x - 7y = 21.
2. Viết nghiệm tổng quát của mỗi phương trình sau và biểu diễn tập nghiệm của nó trên mặt phẳng toạ độ :
a)3x - 4y = 12; b) 5x + 0y = 10 ; c) 0x + 3y = - 9.
3. Tìm một phương trình bậc nhất hai ẩn ax + by = c mà tập nghiệm của nó được biểu diễn bởi đường thẳng song song với trục Ox và cắt trục Oy tại điểm P(0 ; 4).
4. Tìm một phương trình bậc nhất hai ẩn ax + by = c mà tập nghiệm của nó được biểu diễn bởi đường thẳng song song với trục Oy và cắt trục Ox tại điểm Q(-3 ; 0).
5. Tìm một phương trình bậc nhất hai ẩn ax + by = c mà tập nghiệm của nó được biểu diễn bởi đường thẳng đi qua gốc toạ độ và điểm M(-2 ; 4).
Hướng dẫn - Đáp số
1.Giải: a) Cho x = 1. Từ 5.1 + 2y = 7 suy ra 2y = 7 - 5 hay 2y = 2. Do đó y = 1.
Vậy (1 ; 1) là một nghiệm của phương trình.
b) Cho y = 0. Từ 3x - 0.0 = -9 suy ra x = -3. Cặp (-3 ; 0) là một nghiệm của phương trình.
c) Cho x = 0. Từ 0.0 – 1y = 21 suy ra y = -3. Cặp (0 ; -3) là một nghiệm của phương trình.
Trả lời: (h. 12) a) Nghiệm tổng quát:
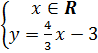 hoặc hoặc 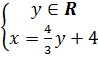 |
|
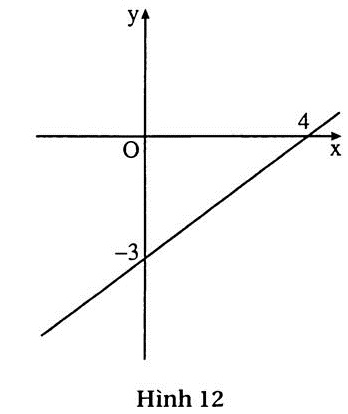
b) (h.13) 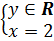
|
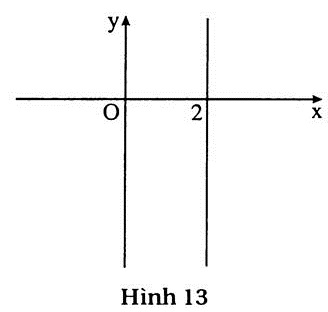
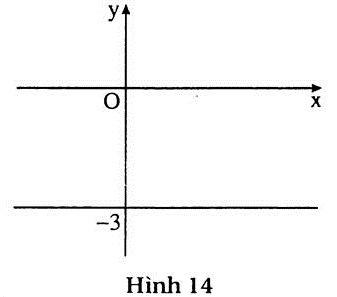
c) (h.14) 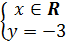
|
3. Giải. Vì tập nghiệm biểu diễn bởi đường thẳng song song với trục Ox nên phương trình có dạng 0x + by = c.
Vì đường thẳng cắt Oy tại điểm P(0 ; 4) nên toạ độ của P thoả mãn phương trình, tức là b.4 = c hay 4b = c. Nếu chọn b = 1, c = 4 thì phương trình 0x + y = 4 có tập nghiệm được biểu diễn bởi đường thẳng đã cho.
4. Giải. Vì tập nghiệm của phương trình được biểu diễn bởi đường thẳng song song với trục Oy nên phương trình có dạng ax + 0y = c.
Vì đường thẳng cắt Ox tại điểm Q(-3 ; 0) nên toạ độ của Q thoả mãn phương trình, tức là a.(-3) = c hay -3a = c. Nếu chọn a = 1, c = -3 thì phương trình x + 0y = -3 có tập nghiệm được biểu diễn bởi đường thẳng đã cho.
5. Giải. Vì tập nghiệm được biểu diễn bởi một đường thẳng đi qua O(0 ; 0) nên a.0 + b.0 = c. Từ đó suy ra c = 0.
Vì đường thẳng đi qua điểm M(-2 ; 4) nên a.(-2) + b.4 = 0 hay -2a + 4b = 0. Suy ra a - 2b. Nếu chọn b = 1, a = 2 thì phương trình 2x + y = 0 có tập nghiệm được biểu diễn bởi đường thẳng đã cho.
© Bản quyền thuộc về
Bài kiểm tra. Ghi rõ nguồn Bài kiểm tra.com khi sao chép nội dung này.
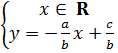
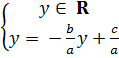
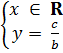
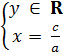
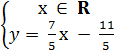
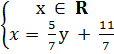
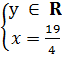




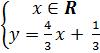
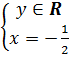
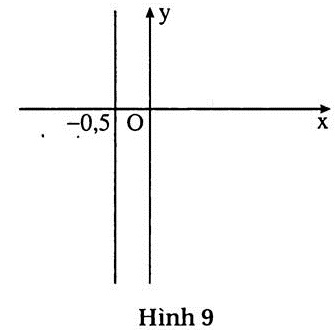
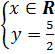

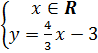 hoặc
hoặc