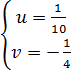Giải bài tập Toán 9, chương III, bài 4: Giải hệ phương trình bằng phương pháp cộng đại số.
2019-08-22T04:00:59-04:00
2019-08-22T04:00:59-04:00
Giải bài tập Toán 9, chương III, bài 4: Giải hệ phương trình bằng phương pháp cộng đại số: Tóm tắt kiến thức, ví dụ, hướng dẫn giải bài tập trong sách giáo khoa và bài tập luyện thêm.
/themes/cafe/images/no_image.gif
Bài Kiểm Tra
https://baikiemtra.com/uploads/bai-kiem-tra-logo.png
Thứ năm - 22/08/2019 04:00
Giải bài tập Toán 9, chương III, bài 4: Giải hệ phương trình bằng phương pháp cộng đại số: Tóm tắt kiến thức, ví dụ, hướng dẫn giải bài tập trong sách giáo khoa và bài tập luyện thêm.
A. Tóm tắt kiến thức
Muốn giải hệ hai phương trình bậc nhất hai ẩn bằng phương pháp cộng đại số, ta làm như sau:
Bước 1. Nhân hai vế của mỗi phương trình với một số thích hợp sao cho các hệ số của một ẩn nào đó trong hệ phương trình là những số bằng nhau (hoặc đối nhau).
Bước 2. Trừ (hoặc cộng) vế với vế hai phương trình để được một phương trình một ẩn. Thay thế một trong hai phương trình của hệ bởi phương trình một ẩn ta được một hệ mới.
Bước 3. Giải phương trình một ẩn ta tìm được giá trị của ẩn đó. Thay giá trị vừa tìm được của ẩn đó vào phương trình còn lại của hệ ta tìm được giá trị tương ứng của ẩn kia. Cặp giá trị tương ứng vừa tìm được của hai ẩn là một nghiệm của hệ phương trình đã cho.
B. Ví dụ
Ví dụ 1. Giải hệ phương trình
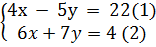 bằng phương pháp cộng đại số.
❖ Phân tích. Nếu làm cho các hệ số của ẩn y đối nhau thì ta phải nhân hai vế của phương trình (1) với 7, của phương trình (2) với 5.
Để làm cho các hệ số của ẩn x bằng nhau ta có thể nhân hai vế của phương trình (1) với 3 và của phương trình (2) với 2. Cách làm thứ hai đơn giản hơn.
Giải. Nhân hai vế của phương trình (1) với 3 ; nhân hai vế của phương trình
(2) với 2, ta được hệ:
bằng phương pháp cộng đại số.
❖ Phân tích. Nếu làm cho các hệ số của ẩn y đối nhau thì ta phải nhân hai vế của phương trình (1) với 7, của phương trình (2) với 5.
Để làm cho các hệ số của ẩn x bằng nhau ta có thể nhân hai vế của phương trình (1) với 3 và của phương trình (2) với 2. Cách làm thứ hai đơn giản hơn.
Giải. Nhân hai vế của phương trình (1) với 3 ; nhân hai vế của phương trình
(2) với 2, ta được hệ:
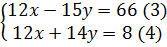 Trừ vế với vế của hai phương trình:
Trừ vế với vế của hai phương trình:
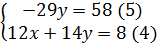 Từ phương trình (5) suy ra y = -2.
Thay y = -2 vào phương trình (4), ta được : 12x +14.(-2) - 8 hay 12x = 36.
Do đó x = 3.
Vậy hệ đã cho có nghiệm duy nhất là (x ; y) = (3 ; -2).
Lưu ý. Có thể trình bày bài giải bằng một dãy những hệ phương trình tương đương như sau :
Từ phương trình (5) suy ra y = -2.
Thay y = -2 vào phương trình (4), ta được : 12x +14.(-2) - 8 hay 12x = 36.
Do đó x = 3.
Vậy hệ đã cho có nghiệm duy nhất là (x ; y) = (3 ; -2).
Lưu ý. Có thể trình bày bài giải bằng một dãy những hệ phương trình tương đương như sau :
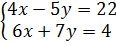 ⇔
⇔ 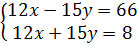 ⇔
⇔ 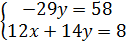 ⇔
⇔ 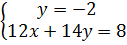 ⇔
⇔ 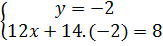 ⇔
⇔ 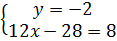 ⇔
⇔ 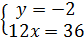 ⇔
⇔ 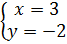 Ví dụ 2. Giải hệ phương trình
Ví dụ 2. Giải hệ phương trình 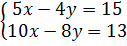 Giải.
Giải.
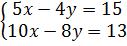 ⇔
⇔ 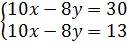 ⇔
⇔ 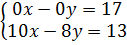 Vì không có giá trị nào của x và y để 0x - 0y = 17 nên phương trình 0x - 0y = 17 vô nghiệm.
Vậy hệ phương trình đã cho vô nghiệm.
Ví dụ 3. Giải hệ phương trình
Vì không có giá trị nào của x và y để 0x - 0y = 17 nên phương trình 0x - 0y = 17 vô nghiệm.
Vậy hệ phương trình đã cho vô nghiệm.
Ví dụ 3. Giải hệ phương trình 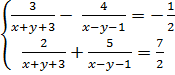 Phân tích. Nếu khử mẫu của các phương trình trong hệ ta sẽ được một hệ phương trình không phải là hệ bậc nhất. Ta chưa biết cách giải hệ phương trình như thế. Song nếu ta đặt ẩn phụ :
u =
Phân tích. Nếu khử mẫu của các phương trình trong hệ ta sẽ được một hệ phương trình không phải là hệ bậc nhất. Ta chưa biết cách giải hệ phương trình như thế. Song nếu ta đặt ẩn phụ :
u = 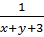 và v =
và v = 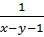 ta sẽ được một hệ phương trình bậc nhất hai ẩn u và v.
Giải hệ này ta tìm được u và v. Từ đó ta lại được hệ bậc nhất hai ẩn x và y.
Giải. Đặt u =
ta sẽ được một hệ phương trình bậc nhất hai ẩn u và v.
Giải hệ này ta tìm được u và v. Từ đó ta lại được hệ bậc nhất hai ẩn x và y.
Giải. Đặt u = 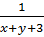 và v =
và v = 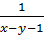 ta được:
ta được:
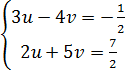 ⇔
⇔ 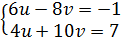 ⇔
⇔ 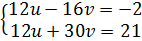 ⇔
⇔ 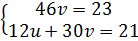 ⇔
⇔ 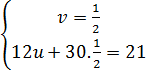 ⇔
⇔ 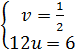 ⇔
⇔ 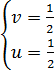 Bây giờ ta có hệ:
Bây giờ ta có hệ:
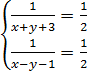 hay
hay 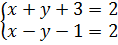 Giải hệ này :
Giải hệ này :
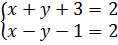 ⇔
⇔ 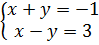 ⇔
⇔ 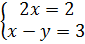 ⇔
⇔ 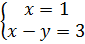 ⇔
⇔ 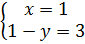 ⇔
⇔ 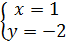 C. Hướng dẫn giải bài tập trong sách giáo khoa
20. Hướng dẫn :
C. Hướng dẫn giải bài tập trong sách giáo khoa
20. Hướng dẫn :
a) Cộng vế với vế hai phương trình.
b) Trừ vế với vế hai phương trình.
c) Nhân hai vế của phương trình thứ hai với 2 rồi trừ vế với vế hai phương trình.
d) Nhân hai vế của phương trình thứ nhất với 3, hai vế của phương trình thứ hai với 2 rồi trừ vế với vế hai phương trình.
e) Nhân hai vế của phương trình thứ nhất với 5 rồi trừ vế với vế hai phương trình.
Đáp số: a) (x ; y) = (2 ; -3); b) (x ; y) = 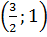 ; c) (x ; y) = (3 ; -2);
d) (x ; y) = (-1 ; 0); e) (x ; y) = (5 ; 3).
21. Giải.
a)
; c) (x ; y) = (3 ; -2);
d) (x ; y) = (-1 ; 0); e) (x ; y) = (5 ; 3).
21. Giải.
a) 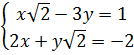 ⇔
⇔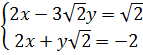 ⇔
⇔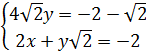 ⇔
⇔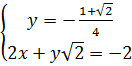 ⇔
⇔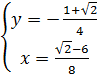 b)
b) 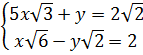 ⇔
⇔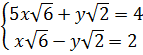 ⇔
⇔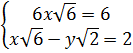 ⇔
⇔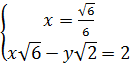 ⇔
⇔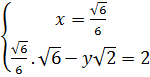 ⇔
⇔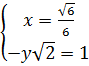 ⇔
⇔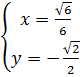 22. Hướng dẫn : a) Nhân hai vế của phương trình thứ nhất với 3, của phương trình thứ hai với 2 rồi cộng vế với vế.
b) Nhân hai vế của phương trình thứ nhất với 2 rồi cộng vế với vế.
c) Nhân hai vế của phương trình thứ hai với 3 rồi trừ vế với vế.
Đáp số: a) (x ; y) =
22. Hướng dẫn : a) Nhân hai vế của phương trình thứ nhất với 3, của phương trình thứ hai với 2 rồi cộng vế với vế.
b) Nhân hai vế của phương trình thứ nhất với 2 rồi cộng vế với vế.
c) Nhân hai vế của phương trình thứ hai với 3 rồi trừ vế với vế.
Đáp số: a) (x ; y) = 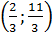 ; b) Vô nghiệm ; c) Vô số nghiệm.
23. Hướng dẫn : Trừ vế với vế.
Đáp số : (x ; y) =
; b) Vô nghiệm ; c) Vô số nghiệm.
23. Hướng dẫn : Trừ vế với vế.
Đáp số : (x ; y) =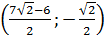 24. Giải. a)
24. Giải. a) 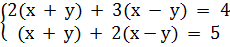 ⇔
⇔ 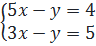 ⇔
⇔ 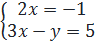 ⇔
⇔ 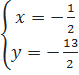 Lưu ý. Cũng có thể giải bằng cách đặt ẩn phụ :u = x + y, v = x - y.
b)
Lưu ý. Cũng có thể giải bằng cách đặt ẩn phụ :u = x + y, v = x - y.
b) 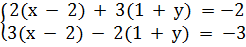 ⇔
⇔ 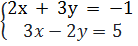 ⇔
⇔ 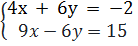 ⇔
⇔ 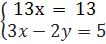 ⇔
⇔ 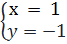 25. Giải. Đa thức P(x) = (3m - 5n + l)x + (4m - n - 10) = 0
25. Giải. Đa thức P(x) = (3m - 5n + l)x + (4m - n - 10) = 0 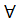 x khi và chỉ khi :
x khi và chỉ khi :
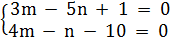 ⇔
⇔ 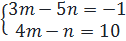 ⇔
⇔ 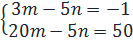 ⇔
⇔ 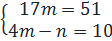 ⇔
⇔ 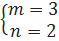 26. Hướng dẫn : Nếu một điểm nằm trên đồ thị của một hàm số thì toạ độ của điểm đó phải thoả mãn hàm số đã cho. Chẳng hạn :
a) Vì đồ thị của hàm số y = ax + b đi qua hai điểm A(2 ; -2) và B(-1 ; 3) nên
26. Hướng dẫn : Nếu một điểm nằm trên đồ thị của một hàm số thì toạ độ của điểm đó phải thoả mãn hàm số đã cho. Chẳng hạn :
a) Vì đồ thị của hàm số y = ax + b đi qua hai điểm A(2 ; -2) và B(-1 ; 3) nên
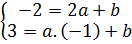 hay
hay 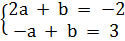 Giải hệ phương trình này với hai ẩn a và b ta được : (a ; b) =
Giải hệ phương trình này với hai ẩn a và b ta được : (a ; b) = 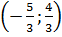 Đáp số: b) (a ; b) =
Đáp số: b) (a ; b) = 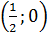 ; c) (a ; b) =
; c) (a ; b) = 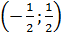 ; d) (a ; b) = (0 ; 2).
27. Giải: a) Đặt u =
; d) (a ; b) = (0 ; 2).
27. Giải: a) Đặt u =  , v =
, v =  ta được hệ phương trình (I)
ta được hệ phương trình (I) 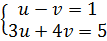 ⇔
⇔ 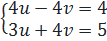 ⇔
⇔ 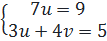 ⇔
⇔ 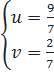 Thay u =
Thay u =  , v =
, v =  ta được x =
ta được x =  , v =
, v =  .
Vậy nghiệm của hệ đã cho là (x ; y) =
.
Vậy nghiệm của hệ đã cho là (x ; y) = 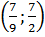 b) Đặt u =
b) Đặt u = 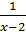 ; v =
; v = 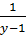 ta được : (II)
ta được : (II) 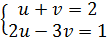 (II) ⇔
(II) ⇔ 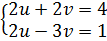 ⇔
⇔ 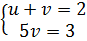 ⇔
⇔ 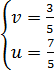 Thay u =
Thay u = 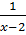 , v =
, v = 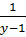 ta được
ta được 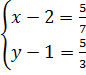 Vậy hệ phương trình đã cho có nghiệm là (x ; y) =
Vậy hệ phương trình đã cho có nghiệm là (x ; y) = 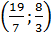 D. Bài tập luyện thêm
1. Giải hệ phương trình :
a)
D. Bài tập luyện thêm
1. Giải hệ phương trình :
a) 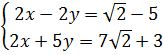 ; b)
; b) 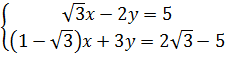 2. Tìm một phương trình bậc nhất hai ẩn sao cho nó có nghiệm là (3 ; -2) và tập nghiệm của nó được biểu diễn bởi một đường thẳng song song với đường thẳng y = 3x - 1.
3. Hãy lập một phương trình bậc nhất hai ẩn sao cho tập nghiệm của nó được biểu diễn bởi một đường thẳng đi qua điểm M(-4 ; 3) và cắt Ox tại điểm N có hoành dộ là 2.
4. Giải hệ phương trình
2. Tìm một phương trình bậc nhất hai ẩn sao cho nó có nghiệm là (3 ; -2) và tập nghiệm của nó được biểu diễn bởi một đường thẳng song song với đường thẳng y = 3x - 1.
3. Hãy lập một phương trình bậc nhất hai ẩn sao cho tập nghiệm của nó được biểu diễn bởi một đường thẳng đi qua điểm M(-4 ; 3) và cắt Ox tại điểm N có hoành dộ là 2.
4. Giải hệ phương trình 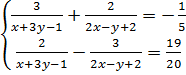 Hướng dẫn - Đáp số
1. Giải.
a)
Hướng dẫn - Đáp số
1. Giải.
a) 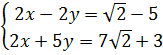 ⇔
⇔ 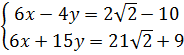 ⇔
⇔ 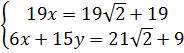 ⇔
⇔ 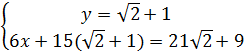 ⇔
⇔ 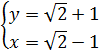 b)
b) 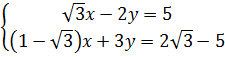 ⇔
⇔ 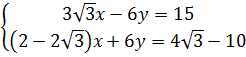 ⇔
⇔ 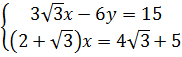 ⇔
⇔ 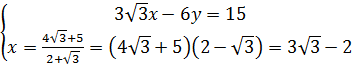 ⇔
⇔ 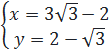 2. Giải. Vì tập nghiệm của phương trình cần tìm là đường thẳng song song với đồ thị y = 3x - 1 nên đường thẳng này cũng có phương trình là y = 3x + b. Vì phương trình này cỏ nghiệm là (3 ; -2) nên -2 = 3.3 + b. Suy ra b = -11.
Vậy phương trình cần tìm là y = 3x - 11 hay 3x - y = 11.
3. Giải. Vì đường biểu diễn tập nghiệm của phương trình cần tìm đi qua điểm M(-4 ; 3) và cắt trục Ox nên nó cắt cả hai trục toạ độ. Do đó nó là đồ thị của hàm số y = ax + b. Vì M(-4 ; 3) và điểm N(2 ; 0) thuộc đồ thị nên
2. Giải. Vì tập nghiệm của phương trình cần tìm là đường thẳng song song với đồ thị y = 3x - 1 nên đường thẳng này cũng có phương trình là y = 3x + b. Vì phương trình này cỏ nghiệm là (3 ; -2) nên -2 = 3.3 + b. Suy ra b = -11.
Vậy phương trình cần tìm là y = 3x - 11 hay 3x - y = 11.
3. Giải. Vì đường biểu diễn tập nghiệm của phương trình cần tìm đi qua điểm M(-4 ; 3) và cắt trục Ox nên nó cắt cả hai trục toạ độ. Do đó nó là đồ thị của hàm số y = ax + b. Vì M(-4 ; 3) và điểm N(2 ; 0) thuộc đồ thị nên
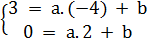 hay
hay 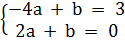 Giải hệ phương trình này ta được : (a ; b) =
Giải hệ phương trình này ta được : (a ; b) = 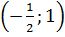 Vậy phương trình cần tìm là y = -
Vậy phương trình cần tìm là y = -  x + 1 hay x + 2y = 2.
4. Giải. Đặt u =
x + 1 hay x + 2y = 2.
4. Giải. Đặt u = 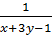 ; v =
; v = 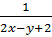 ta được hệ phương trình
(I)
ta được hệ phương trình
(I) 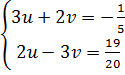 Ta có: (I) ⇔
Ta có: (I) ⇔ 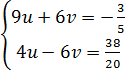 ⇔
⇔ 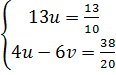 ⇔
⇔ 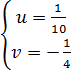 Thay u =
Thay u = 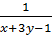 ; v =
; v = 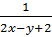 ta được hệ phương trình
ta được hệ phương trình
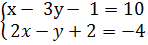 hay
hay 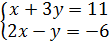 Giải hệ phương trình này ta được (x ; y) = (-1 ; 4).
Giải hệ phương trình này ta được (x ; y) = (-1 ; 4).
© Bản quyền thuộc về
Bài kiểm tra. Ghi rõ nguồn Bài kiểm tra.com khi sao chép nội dung này.
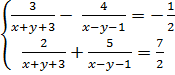
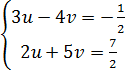 ⇔
⇔ 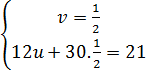 ⇔
⇔ 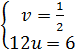 ⇔
⇔ 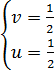
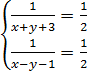 hay
hay 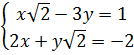 ⇔
⇔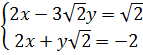 ⇔
⇔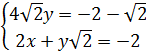
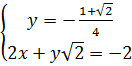 ⇔
⇔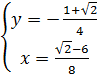
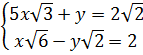 ⇔
⇔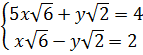 ⇔
⇔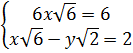
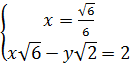 ⇔
⇔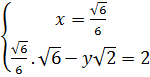 ⇔
⇔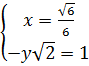 ⇔
⇔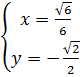
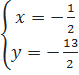
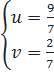
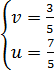
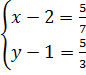
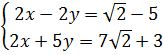 ; b)
; b) 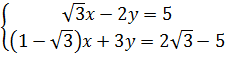
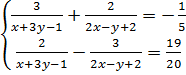
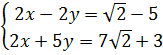 ⇔
⇔ 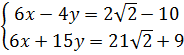 ⇔
⇔ 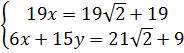
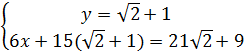 ⇔
⇔ 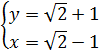
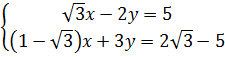 ⇔
⇔ 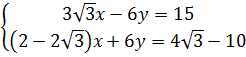
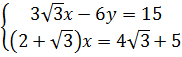 ⇔
⇔ 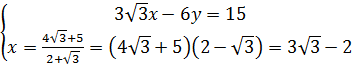
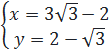
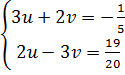
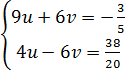 ⇔
⇔ 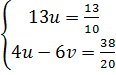 ⇔
⇔