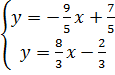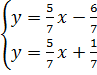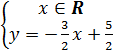Giải bài tập Toán 9, chương III, bài 2: Hệ hai phương trình bậc nhất hai ẩn
2019-08-22T04:02:19-04:00
2019-08-22T04:02:19-04:00
Giải bài tập Toán 9, chương III, bài 2: Hệ hai phương trình bậc nhất hai ẩn: Tóm tắt kiến thức, ví dụ, hướng dẫn giải bài tập trong sách giáo khoa và bài tập luyện thêm.
/themes/cafe/images/no_image.gif
Bài Kiểm Tra
https://baikiemtra.com/uploads/bai-kiem-tra-logo.png
Thứ tư - 21/08/2019 04:10
Giải bài tập Toán 9, chương III, bài 2: Hệ hai phương trình bậc nhất hai ẩn: Tóm tắt kiến thức, ví dụ, hướng dẫn giải bài tập trong sách giáo khoa và bài tập luyện thêm.
A. Tóm tắt kiến thức
1. Khái niệm về hệ hai phương trình bậc nhất hai ẩn
Với hai phương trình bậc nhất hai ẩn ax + by = c và a’x + b’y = c’ ta có một hệ hai phương trình bậc nhất hai ẩn
(I) 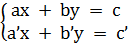 Mỗi nghiệm chung của hai phương trình trong hệ được gọi là một nghiệm của hệ. Nếu hai phương trình trong hệ không có nghiệm chung thì ta nói hệ vô nghiệm. Giải hệ phương trình (I) là tìm tất cả các nghiệm của nó.
2. Minh hoạ hình học tập nghiệm của hệ phương trình bậc nhất hai ẩn
Tập nghiệm của mỗi phương trình trong hệ (I) được biểu diễn bởi một đường thẳng trong mặt phẳng toạ độ. Do đó, trên cùng một mặt phẳng toạ độ, mỗi nghiệm của hệ (I) được biểu diễn bởi một điểm chung của hai đường thẳng (d) : ax + by = c và (d’) : a’x + b’y = c’.
Vì vậy :
- Nếu (d) cắt (d’) thì hệ có một nghiệm duy nhất và tập nghiệm của hệ được biểu diễn bởi giao điểm của (d) và (d’).
- Nếu (d) // (d’) thì hệ vô nghiệm và tập nghiệm là tập rỗng.
- Nếu (d) trùng với (d’) thì hệ có vô số nghiệm và tập nghiệm được biểu diễn bởi (d).
3. Hai hệ phương trình tương đương
Hai hệ phương trình được gọi là tương đương nếu chúng có cũng một tập nghiệm.
B. Ví dụ
Ví dụ 1. Xét xem mỗi cặp số (-2 ; 7), (3 ; -5) có phải là nghiệm của hệ phương trình:
Mỗi nghiệm chung của hai phương trình trong hệ được gọi là một nghiệm của hệ. Nếu hai phương trình trong hệ không có nghiệm chung thì ta nói hệ vô nghiệm. Giải hệ phương trình (I) là tìm tất cả các nghiệm của nó.
2. Minh hoạ hình học tập nghiệm của hệ phương trình bậc nhất hai ẩn
Tập nghiệm của mỗi phương trình trong hệ (I) được biểu diễn bởi một đường thẳng trong mặt phẳng toạ độ. Do đó, trên cùng một mặt phẳng toạ độ, mỗi nghiệm của hệ (I) được biểu diễn bởi một điểm chung của hai đường thẳng (d) : ax + by = c và (d’) : a’x + b’y = c’.
Vì vậy :
- Nếu (d) cắt (d’) thì hệ có một nghiệm duy nhất và tập nghiệm của hệ được biểu diễn bởi giao điểm của (d) và (d’).
- Nếu (d) // (d’) thì hệ vô nghiệm và tập nghiệm là tập rỗng.
- Nếu (d) trùng với (d’) thì hệ có vô số nghiệm và tập nghiệm được biểu diễn bởi (d).
3. Hai hệ phương trình tương đương
Hai hệ phương trình được gọi là tương đương nếu chúng có cũng một tập nghiệm.
B. Ví dụ
Ví dụ 1. Xét xem mỗi cặp số (-2 ; 7), (3 ; -5) có phải là nghiệm của hệ phương trình: 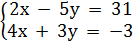 hay không.
Phân tích. Vì một nghiệm của hệ đã cho phải là nghiệm chung của cả hai phương trình trong hệ nên ta phải kiểm tra xem cặp số (-2 ; 7) có phải là một nghiệm của mỗi phương trình trong hệ hay không.
Giải. Thay x = -2, y = 7 vào phương trình đầu ta được :
2.(-2) - 5.7 = -4 - 35 = -39
hay không.
Phân tích. Vì một nghiệm của hệ đã cho phải là nghiệm chung của cả hai phương trình trong hệ nên ta phải kiểm tra xem cặp số (-2 ; 7) có phải là một nghiệm của mỗi phương trình trong hệ hay không.
Giải. Thay x = -2, y = 7 vào phương trình đầu ta được :
2.(-2) - 5.7 = -4 - 35 = -39 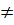 31.
Điều này chứng tỏ (-2 ; 7) không phải là một nghiệm của phương trình đầu nên nó không phải là một nghiệm của hệ phương trình đã cho.
+ Thay x = 3, y = -5 vào phương trình đầu, ta được :
- 5.(-5) = 6 + 25 = 31.
+ Thay x = 3, y = -5 vào phương trình thứ hai, ta được :
4. 3 + 3.(-5) = 12- 15 = - 3.
❖ Các kết quả vừa được chứng tỏ rằng cặp số (3 ; -5) là một nghiệm của hệ phương trình đã cho.
Ví dụ 2. Xét xem mỗi cặp số (4 ; -3), (-2 ; -18) có phải là những nghiệm của hệ phương trình:
31.
Điều này chứng tỏ (-2 ; 7) không phải là một nghiệm của phương trình đầu nên nó không phải là một nghiệm của hệ phương trình đã cho.
+ Thay x = 3, y = -5 vào phương trình đầu, ta được :
- 5.(-5) = 6 + 25 = 31.
+ Thay x = 3, y = -5 vào phương trình thứ hai, ta được :
4. 3 + 3.(-5) = 12- 15 = - 3.
❖ Các kết quả vừa được chứng tỏ rằng cặp số (3 ; -5) là một nghiệm của hệ phương trình đã cho.
Ví dụ 2. Xét xem mỗi cặp số (4 ; -3), (-2 ; -18) có phải là những nghiệm của hệ phương trình: 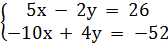 hay không. Hỏi hệ phương trình này có bao nhiêu nghiệm ?
Giải. Thay x = 4, y = -3 vào mỗi phương trình, ta được :
5.4 - 2.(-3) = 20 + 6 = 26 ;
-10.4 + 4.(-3) = -40 - 12 = -52.
Điều này chứng tỏ cặp số (4 ; -3) là một nghiệm của hệ phương trình đã cho.
+ Thay x = -2 ; y = -18 vào mỗi phương trình ta được :
5.(-2) - 2.(-18) = -10 + 36 = 26 ;
-10.(-2) + 4.(-18) = 20 - 72 = -52.
Điều này chứng tỏ cặp số (-2 ; -18) là một nghiệm của hệ phương trình đã cho. Vì hai cặp số (4 ; -3) và (-2 ; -18) là hai nghiệm của mỗi phương trình và tập nghiệm của mỗi phương trình được biểu diễn bởi một đường thẳng nên mỗi đường thẳng này đều đi qua hai điểm A(4 ; -3) và B(-2 ; -18). Như vậy hai đường thẳng biểu diễn tập nghiệm của hai phương trình trùng nhau. Vậy hệ đã cho có vô số nghiệm.
Ví dụ 3. Minh hoạ hình học tập nghiệm của mỗi hệ phương trình sau :
a)
hay không. Hỏi hệ phương trình này có bao nhiêu nghiệm ?
Giải. Thay x = 4, y = -3 vào mỗi phương trình, ta được :
5.4 - 2.(-3) = 20 + 6 = 26 ;
-10.4 + 4.(-3) = -40 - 12 = -52.
Điều này chứng tỏ cặp số (4 ; -3) là một nghiệm của hệ phương trình đã cho.
+ Thay x = -2 ; y = -18 vào mỗi phương trình ta được :
5.(-2) - 2.(-18) = -10 + 36 = 26 ;
-10.(-2) + 4.(-18) = 20 - 72 = -52.
Điều này chứng tỏ cặp số (-2 ; -18) là một nghiệm của hệ phương trình đã cho. Vì hai cặp số (4 ; -3) và (-2 ; -18) là hai nghiệm của mỗi phương trình và tập nghiệm của mỗi phương trình được biểu diễn bởi một đường thẳng nên mỗi đường thẳng này đều đi qua hai điểm A(4 ; -3) và B(-2 ; -18). Như vậy hai đường thẳng biểu diễn tập nghiệm của hai phương trình trùng nhau. Vậy hệ đã cho có vô số nghiệm.
Ví dụ 3. Minh hoạ hình học tập nghiệm của mỗi hệ phương trình sau :
a) 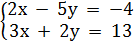 b)
b) 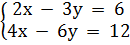 c)
c) 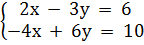 Phân tích. Để minh hoạ hình học tập nghiệm của mỗi hệ phương trình, ta phải vẽ hai đường thẳng biểu diễn hai tập nghiệm của hai phương trình trong mỗi hệ.
Phân tích. Để minh hoạ hình học tập nghiệm của mỗi hệ phương trình, ta phải vẽ hai đường thẳng biểu diễn hai tập nghiệm của hai phương trình trong mỗi hệ.
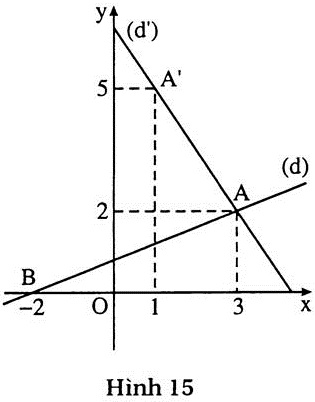
Giải. a) (h.15)
+ Vẽ đường thẳng (d) : 2x - 5y = -4.
Cho y = 2, từ 2x - 5.2 = - 4 suy ra 2x = 6.
Do đó x = 3.
Đường thằng (d) đi qua điểm A(3 ; 2).
Cho y = 0, từ 2x - 5.0 = - 4 suy ra 2x = - 4.
Do đó x = -2.
Đường thẳng (d) đi qua điểm B(-2 ; 0). |
|
+ Vẽ đường thẳng (d’) : 3x + 2y = 13.
Cho x = 1, từ 3.1 + 2y = 13 suy ra y = 5.
Đường thẳng (d’) đi qua điểm A’(1 ; 5).
Cho x = 3, từ 3.3 + 2y = 13 suy ra 2y = 4.
Do đó y = 2.
Đường thẳng (d’) đi qua điểm A(3 ; 2).
Tập nghiệm của hệ được biểu diễn bởi giao
điểm A(3 ; 2).
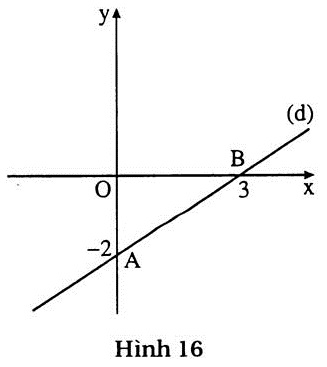
b) (h.16)
Vẽ đường thẳng (d): 2x - 3y = 6.
Cho x = 0, từ 2.0 - 3y = 6 suy ra y = - 2.
Cho y = 0, từ 2x - 3.0 = 6 suy ra x = 3.
Đường thẳng (d) đi qua hai điểm A (0; - 2) và B(3; 0)
+ Vẽ đường thẳng (d’): 4x – 6y = 12
Vì phương trình 4x - 6y - 12 tương đương với phương trình 2x - 3y = 6 nên (d’) trùng với (d).
Tập nghiệm của hệ được biểu diễn bởi đường thẳng (d). |
|
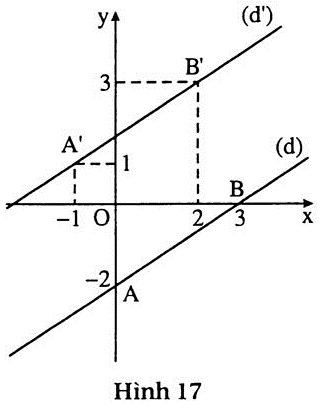
c) (h.17)
- Vẽ đường thẳng (d): 2x - 3y = 6 (theo câu b).
- Vẽ đường thẳng (d’) : -4x + 6y = 10.
Cho x = -1, từ -4.(-1) + 6y = 10 suy ra y = 1.
Cho x - 2, từ -4.2 + 6y = 10 suy ra y = 3.
Đường thằng (d’) đi qua hai điểm A’(-1; 1)và B’(2; 3).
Tập nghiệm của hệ này là tập rỗng. |
|
Ví dụ 4. Không vẽ hình hãy nhận xét số nghiệm của mỗi hệ phương trình sau
a) 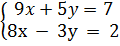 b)
b) 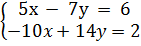 c)
c) 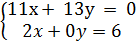 Phân tích. Muốn biết số nghiệm của hệ phương trình bậc nhất hai ẩn ta chỉ cần biết vị trí tương đối giữa hai đường thẳng biểu diễn tập nghiệm của hai phương trình trong hệ.
Giải: a) Hệ đã cho tương đương với hệ
Phân tích. Muốn biết số nghiệm của hệ phương trình bậc nhất hai ẩn ta chỉ cần biết vị trí tương đối giữa hai đường thẳng biểu diễn tập nghiệm của hai phương trình trong hệ.
Giải: a) Hệ đã cho tương đương với hệ 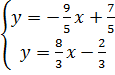 Vì
Vì 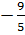
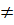
 nên hai đường thẳng
nên hai đường thẳng 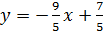 và
và 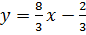 cắt nhau.
Vậy hệ đã cho có một nghiệm duy nhất.
b) Hệ đã cho tương đương với hệ
cắt nhau.
Vậy hệ đã cho có một nghiệm duy nhất.
b) Hệ đã cho tương đương với hệ 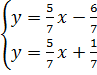 Vì
Vì  =
=  và
và 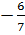
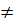
 nên hai đường thẳng y=
nên hai đường thẳng y=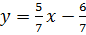 và
và 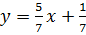 song song. Vậy hệ đã cho vô nghiệm.
c) Vì đường thẳng 11x - 13y = 0 cắt hai trục toạ độ và đường thẳng 2x + 0y = 6 song song với trục Oy nên hai đường thẳng này cắt nhau. Vậy hệ đã cho có một nghiệm duy nhất.
C. Hướng dẫn giải bài tập trong sách giáo khoa
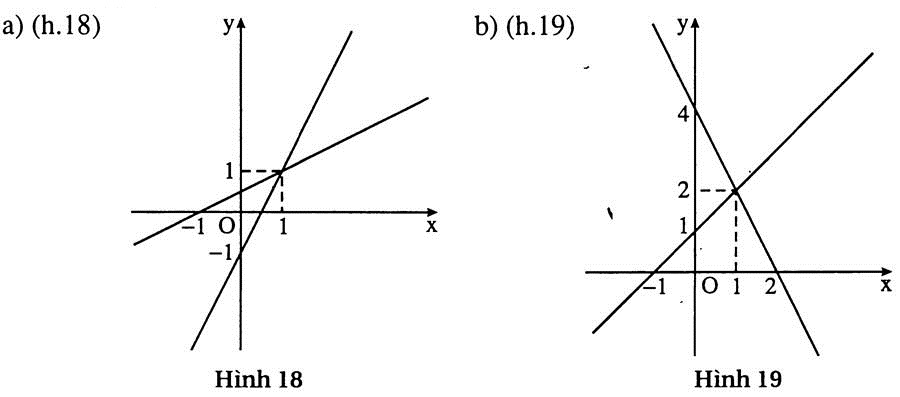
4. Trả lời: a) Một nghiệm vì hai đường thẳng y = 3 - 2x và y = 3x - 1 cắt nhau.
b) Vô nghiệm vì hai đường thẳng y = -
song song. Vậy hệ đã cho vô nghiệm.
c) Vì đường thẳng 11x - 13y = 0 cắt hai trục toạ độ và đường thẳng 2x + 0y = 6 song song với trục Oy nên hai đường thẳng này cắt nhau. Vậy hệ đã cho có một nghiệm duy nhất.
C. Hướng dẫn giải bài tập trong sách giáo khoa
4. Trả lời: a) Một nghiệm vì hai đường thẳng y = 3 - 2x và y = 3x - 1 cắt nhau.
b) Vô nghiệm vì hai đường thẳng y = -  x + 3 và y = -
x + 3 và y = -  x + 1 song song.
c) Một nghiệm vì hai đường thẳng 2y = -3x và 3y = 2x chính là hai đường thẳng y = -
x + 1 song song.
c) Một nghiệm vì hai đường thẳng 2y = -3x và 3y = 2x chính là hai đường thẳng y = -  x và y =
x và y =  x và chúng cắt nhau.
d) Vô số nghiệm vì hai đường thẳng 3x - y = 3 và x -
x và chúng cắt nhau.
d) Vô số nghiệm vì hai đường thẳng 3x - y = 3 và x -  y = 1 chính là cùng một đường thẳng y = 3x - 3.
5. Hướng dẫn : Vẽ hai đường thẳng biểu diễn các tập nghiệm của hai phương trình trong hệ.
6. Trả lời : Bạn Nga nói đúng. Hai hệ phương trình bậc nhất hai ẩn cùng vô nghiệm thì tập nghiệm của chúng đều là tập rỗng ; nghĩa là chúng có cùng tập nghiệm. Do đó chúng tương đương.
Bạn Phương nói sai. Ví dụ hai hệ phương trình :
(I)
y = 1 chính là cùng một đường thẳng y = 3x - 3.
5. Hướng dẫn : Vẽ hai đường thẳng biểu diễn các tập nghiệm của hai phương trình trong hệ.
6. Trả lời : Bạn Nga nói đúng. Hai hệ phương trình bậc nhất hai ẩn cùng vô nghiệm thì tập nghiệm của chúng đều là tập rỗng ; nghĩa là chúng có cùng tập nghiệm. Do đó chúng tương đương.
Bạn Phương nói sai. Ví dụ hai hệ phương trình :
(I) 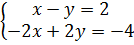 và (II)
và (II) 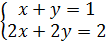 là hai hệ có vô số nghiệm ; nhưng tập nghiệm của hệ (I) được biểu diễn bởi đường thẳng y = x - 2 còn tập nghiệm của hệ (II) được biểu diễn bởi đường thẳng y = -x + 1. Như vậy hai hệ này có tập nghiệm khác nhau.
7. Trả lời : a) Nghiệm tổng quát của phương trình 2x + y = 4 là
là hai hệ có vô số nghiệm ; nhưng tập nghiệm của hệ (I) được biểu diễn bởi đường thẳng y = x - 2 còn tập nghiệm của hệ (II) được biểu diễn bởi đường thẳng y = -x + 1. Như vậy hai hệ này có tập nghiệm khác nhau.
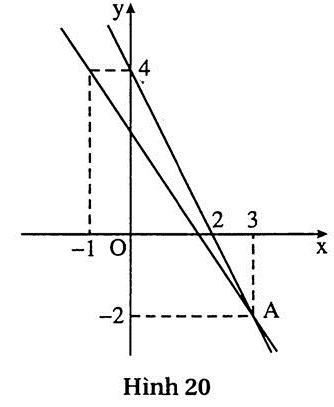
7. Trả lời : a) Nghiệm tổng quát của phương trình 2x + y = 4 là 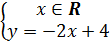 Nghiệm tổng quát của phương trình 3x + 2y = 5 là
Nghiệm tổng quát của phương trình 3x + 2y = 5 là 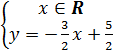 b) (h.20) Nghiệm chung của chúng là A(3; -2)
8. Giải:
b) (h.20) Nghiệm chung của chúng là A(3; -2)
8. Giải:
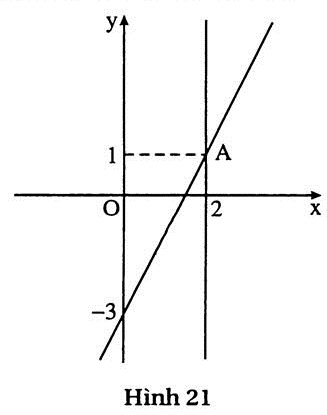
| a) (h.21) Vì đường thẳng x = 2 song song với trục Oy, đường thẳng 2x - y = 3 cắt hai trục toạ độ nên hai đường thẳng này cắt nhau. Do đó hệ có nghiệm duy nhất. Nghiệm của hệ là A(2 ; 1).
|
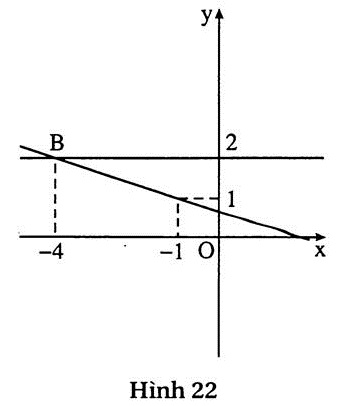
b) (h.22) Hệ có nghiệm duy nhất vì đường thẳng x + 3y = 2 cắt hai trục toạ độ, đường thẳng 2y - 4 song song với trục Ox. Nghiệm của hệ là B(- 4 ; 2).
|
9. Trả lời : a) Vô nghiệm. Đường thẳng 3x + 3y = 2 chính là đường thẳng y = -x +  ; đường thẳng x + y = 2 chính là đường thăng y = -x + 2 mà hai đường thẳng này song song với nhau.
b) Vô nghiệm. Đường thẳng 3x - 2y = 1 chính là đường thẳng y =
; đường thẳng x + y = 2 chính là đường thăng y = -x + 2 mà hai đường thẳng này song song với nhau.
b) Vô nghiệm. Đường thẳng 3x - 2y = 1 chính là đường thẳng y =  x -
x -  ; đường thẳng -6x + 4y = 0 chính là đường thẳng y =
; đường thẳng -6x + 4y = 0 chính là đường thẳng y =  x. Hai đường thẳng này song song với nhau.
10. Trả lời : a) Vô số nghiệm. Hai đường thẳng 4x - 4y = 2 và -2x + 2y = -1 đều là đường thẳng y = x -
x. Hai đường thẳng này song song với nhau.
10. Trả lời : a) Vô số nghiệm. Hai đường thẳng 4x - 4y = 2 và -2x + 2y = -1 đều là đường thẳng y = x -  b) Vô số nghiệm. Hai đường thẳng
b) Vô số nghiệm. Hai đường thẳng  x - y =
x - y =  và x - 3y = 2 đều là đường thẳng y =
và x - 3y = 2 đều là đường thẳng y =  x -
x -  11. Trả lời. Nếu hệ phương trình có hai nghiệm phân biệt thì hai nghiệm ấy đều là nghiệm của mỗi phương trình trong hệ. Do đó hai điểm biểu diễn bởi hai nghiệm ấy đều thuộc đường thẳng biểu diễn mỗi tập nghiệm. Như vậy hai đường thẳng này có hai điểm chung. Suy ra chúng trùng nhau. Vậy hệ có vô số nghiệm.
D. Bài tập luyện thêm
1. Tìm a và b để hệ phương trình
11. Trả lời. Nếu hệ phương trình có hai nghiệm phân biệt thì hai nghiệm ấy đều là nghiệm của mỗi phương trình trong hệ. Do đó hai điểm biểu diễn bởi hai nghiệm ấy đều thuộc đường thẳng biểu diễn mỗi tập nghiệm. Như vậy hai đường thẳng này có hai điểm chung. Suy ra chúng trùng nhau. Vậy hệ có vô số nghiệm.
D. Bài tập luyện thêm
1. Tìm a và b để hệ phương trình 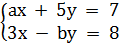 có một nghiệm là (-1 ; 1).
Với giá trị vừa tìm được của a và b thì hệ phương trình có bao nhiêu nghiệm ?
2. Không vẽ hình hãy cho biết số nghiệm của mỗi hệ phương trình sau :
3. Tìm a và b để hệ phương trình
có một nghiệm là (-1 ; 1).
Với giá trị vừa tìm được của a và b thì hệ phương trình có bao nhiêu nghiệm ?
2. Không vẽ hình hãy cho biết số nghiệm của mỗi hệ phương trình sau :
3. Tìm a và b để hệ phương trình 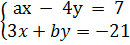 có vô số nghiệm.
4. Tìm a và c để hệ phương trình
có vô số nghiệm.
4. Tìm a và c để hệ phương trình 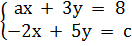 vô nghiệm.
5. Với giá trị nào của a và b thì hệ phương trình
vô nghiệm.
5. Với giá trị nào của a và b thì hệ phương trình 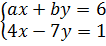 có nghiệm duy nhất ?
6. Tìm giá trị của a và b để hệ phương trình
có nghiệm duy nhất ?
6. Tìm giá trị của a và b để hệ phương trình 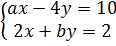 tương đương với hệ phương trình
tương đương với hệ phương trình 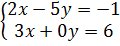 Hướng dẫn - Đáp số
1. Giải. Để (-1 ; 1) là nghiệm của hệ phương trình thì:
Hướng dẫn - Đáp số
1. Giải. Để (-1 ; 1) là nghiệm của hệ phương trình thì:
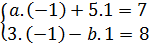 hay
hay 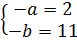 hay
hay 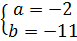 Vậy hệ đã cho là:
Vậy hệ đã cho là: 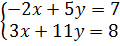 Vì các đường thẳng -2x + 5y = 7 và 3x + 11y = 8 lần lượt là các đường thẳng
y =
Vì các đường thẳng -2x + 5y = 7 và 3x + 11y = 8 lần lượt là các đường thẳng
y =  x +
x +  và y = -
và y = - 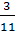 x +
x +  , do
, do 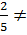 -
- 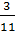 nên chúng cắt nhau. Do đó hệ chỉ có một nghiệm.
2. Trả lời: a) Có một nghiệm. b) Vô số nghiệm
c) Vô nghiệm. d) Có một nghiệm
3. Giải. Muốn cho hệ phương trình
nên chúng cắt nhau. Do đó hệ chỉ có một nghiệm.
2. Trả lời: a) Có một nghiệm. b) Vô số nghiệm
c) Vô nghiệm. d) Có một nghiệm
3. Giải. Muốn cho hệ phương trình 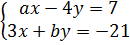 có vô số nghiệm thì tập nghiệm của hai phương trình trong hệ phải được biểu diễn bởi cùng một đường thẳng.
Đường thẳng ax - 4y = 7 chính là đường thẳng (d) : y =
có vô số nghiệm thì tập nghiệm của hai phương trình trong hệ phải được biểu diễn bởi cùng một đường thẳng.
Đường thẳng ax - 4y = 7 chính là đường thẳng (d) : y = x -
x -  .
Để đường thẳng 3x + by = -21 cũng là đường thẳng (d) thì b
.
Để đường thẳng 3x + by = -21 cũng là đường thẳng (d) thì b 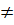 0 và
(d): y = -
0 và
(d): y = -  x -
x - 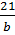 .
Do đó
.
Do đó  = -
= -  và
và  =
= 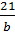 . Suy ra b = 12 và a = -1.
4. Giải. Muốn cho hệ phương trình
. Suy ra b = 12 và a = -1.
4. Giải. Muốn cho hệ phương trình 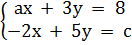 vô nghiệm thì hai đường thẳng biểu diễn các tập nghiệm của hai phương trình trong hệ song song với nhau.
Đường thẳng ax + 3y = 8 chính là đường thẳng (d): y = -
vô nghiệm thì hai đường thẳng biểu diễn các tập nghiệm của hai phương trình trong hệ song song với nhau.
Đường thẳng ax + 3y = 8 chính là đường thẳng (d): y = - 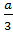 x +
x +  Đường thẳng -2x + 5y = c chính là đường thẳng (d’):y =
Đường thẳng -2x + 5y = c chính là đường thẳng (d’):y =  x +
x +  .
Để (d) // (d’) thì -
.
Để (d) // (d’) thì - 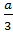 =
=  và
và 
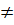
 hay a = -
hay a = -  và c
và c 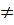
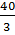 Vậy hệ vô nghiệm khi a = -
Vậy hệ vô nghiệm khi a = -  và c
và c 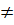
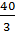 5. Muốn cho hệ phương trình
5. Muốn cho hệ phương trình 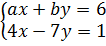 có nghiệm duy nhất thì hai đường thẳng biểu diễn các tập nghiệm của hai phương trình trong hệ cắt nhau.
Đường thẳng 4x - 7y = 1 chính là đường thẳng (d) : y =
có nghiệm duy nhất thì hai đường thẳng biểu diễn các tập nghiệm của hai phương trình trong hệ cắt nhau.
Đường thẳng 4x - 7y = 1 chính là đường thẳng (d) : y =  x -
x -  . Nó cắt cả hai trục.
Do đó nếu a = 0 thì hệ có nghiệm duy nhất với mọi b
. Nó cắt cả hai trục.
Do đó nếu a = 0 thì hệ có nghiệm duy nhất với mọi b 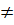 0.
Tương tự, nếu b = 0 thì hệ có nghiệm duy nhất với mọi a
0.
Tương tự, nếu b = 0 thì hệ có nghiệm duy nhất với mọi a 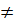 0.
Nếu a
0.
Nếu a 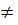 0 và b
0 và b 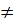 0 thì đường thẳng ax + by = 6 chính là đường thẳng
(d’): y = -
0 thì đường thẳng ax + by = 6 chính là đường thẳng
(d’): y = - x +
x +  .
Để (d) và (d’) cắt nhau thì -
.
Để (d) và (d’) cắt nhau thì - 
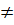
 hay a
hay a 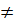
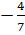 b.
Để ý rằng nếu a
b.
Để ý rằng nếu a 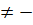
 b thì a
b thì a 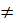 0 khi b = 0 và b
0 khi b = 0 và b 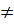 0 khi a = 0. Vì thế ta có kết luận chung :
Hệ đã cho có nghiệm duy nhất khi a
0 khi a = 0. Vì thế ta có kết luận chung :
Hệ đã cho có nghiệm duy nhất khi a 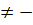
 b
6. Giải. Vì đường thẳng 3x + 0y = 6 chính là đường thẳng x + 0y = 2 ; nó song . song với Oy và cắt Ox tại điểm Q(2 ; 0). Do đó nó cũng cắt đường thẳng 2x - 5y = -1 tại điểm M(2 ; y0). Khi đó 2.2 - 5y0 = -1 hay 5y0 = 5.
Suy ra y0 = 1.
Vì toạ độ giao điểm M(2 ; 1) của hai đường thẳng là nghiệm của hệ phương trình
b
6. Giải. Vì đường thẳng 3x + 0y = 6 chính là đường thẳng x + 0y = 2 ; nó song . song với Oy và cắt Ox tại điểm Q(2 ; 0). Do đó nó cũng cắt đường thẳng 2x - 5y = -1 tại điểm M(2 ; y0). Khi đó 2.2 - 5y0 = -1 hay 5y0 = 5.
Suy ra y0 = 1.
Vì toạ độ giao điểm M(2 ; 1) của hai đường thẳng là nghiệm của hệ phương trình
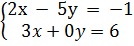 nên hệ này có nghiệm duy nhất là (2 ; 1).
Để hệ
nên hệ này có nghiệm duy nhất là (2 ; 1).
Để hệ 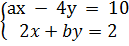 tương đương với hệ phương trình
tương đương với hệ phương trình 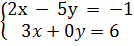 thì (2 ; 1) cũng là nghiệm duy nhất của hệ
thì (2 ; 1) cũng là nghiệm duy nhất của hệ 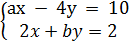 Muốn vậy ta phải có
Muốn vậy ta phải có 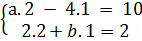 Suy ra
Suy ra 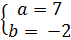 Vậy hai hệ đã cho tương đương khi a = 7, b = -2
Vậy hai hệ đã cho tương đương khi a = 7, b = -2
© Bản quyền thuộc về
Bài kiểm tra. Ghi rõ nguồn Bài kiểm tra.com khi sao chép nội dung này.