Giải bài tập Toán 9: Ôn tập chương II

Bài 1. a) Với những giá trị nào của m thì hàm số bậc nhất y = (m - 1)x + 3 đồng biến?
b) Với những giá trị nào của k thì hàm số bậc nhất y = (5 - k)x + 1 nghịch biến?

Giải:

(m - 1)x + 3 là hàm số bậc nhất đối với x khi  m – 1 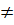0 hay m 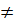1 . Do đó hàm số đồng biến khi hệ số của x là dương, nghĩa là: m -1 > 0 ⇔  m > 1
Vậy khi m > 1 thì hàm số y = (m - 1)x + 3 đồng biến.

b) Hàm số y = (5 - k)x + 1  là hàm số bậc nhất đối với x khi 5 - k 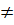0 hay k 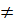5 do đó, hàm số nghịch biến khi hệ số của x âm, nghĩa là: 5 – k < 0 ⇔ k > 5
Vậy khi k > 5 thì hàm số y = (5 - k)x + 1 nghịch biến

Bài 2. Với những giá trị nào của m thì đồ thị các hàm số y = 2x + (3 + m) và y = 3x + (5 - m) cắt nhau tại một điểm trên trục tung?

Giải:

Các hàm số y = 2x + (3 + m) và y = 3x + (5 - m) đều là hàm số bậc nhất đối với x và hệ số của x đều khác 0. Đồ thị của chúng là các đường thẳng cắt trục tung tại một điểm có tung độ là b. Do đó, hai đường thẳng cắt nhau tại cùng một điểm trên trục tung, khi và chỉ khi tung độ gốc của chúng bằng nhau, nghĩa là:
3 + m = 5 – m ⇔ m = l Vậy khi m = 1 thì hai đường thẳng đã cho cắt nhau tại một điểm trên trục tung.

Bài 3. Tìm giá trị của a để hai đường thẳng y = (a - 1)x + 2 (a 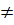1) và y = (3 - a)x + 1 (a 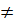3) song song với nhau.
 
Giải:

Hai đường thẳng y = (a - 1)x + 2 và y = (3 - a)x + 1 có tung độ gốc khác nhau (2 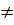1), do đó chúng khi hệ số của x bằng nhau, nghĩa là:
a - 1 = 3 – a ⇔ a = 2.
Vậy khi a = 2 thì hai dường thẳng song song với nhau.

Bài 4. Xác định k và m để hai dường thẳng sau đây trùng nhau:
y = kx + (m - 2) (k 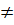0);    y = (5 - k)x + (4 - m) (k  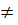 5).

Giải:

Hai đường thẳng y = kx + (m - 2) và y = (5 - k)x + (4 - m) trùng nhau khi và chỉ khi:
 
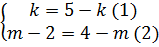Từ (1), ta có: 2k = 5 ⇔ k = 2,5
Từ (2), ta có: 2m = 6 ⇔ m = 3
Vậy điều kiện để hai đường thẳng trùng nhau là: k = 2,5 và m = 3.

Bài 5. a) Vẽ đồ thị hai hàm số sau trên cùng hệ trục tọa độ:
y = 0,5x + 2 (1);    y = 5 - 2x (2).

b) Gọi giao điểm của các đường thẳng (1) và (2) với trục hoành thứ tự là A, B và gọi giao điểm của hai đường thẳng đó là C. Tìm tọa độ của các điểm A, B, C.

c) Tính các khoảng cách AB, AC và BC (đơn vị đo trên trục tọa độ là xentirnét, làm tròn đến chữ số thập phân thứ hai).

d) Tính các góc tạo bởi các đường thẳng có phương trình (1) và (2) với trục Ox (làm tròn đến phút).

Giải:

a) Đồ thị, xem hình vẽ b) Dễ thấy A(-4; 0); B(2,5; 0) Hoành độ của C là nghiệm của phương trình: 0,5x + 2 = 5 – 2x ⇒ x =  = 1,2 Ta tính được y = 2,6.

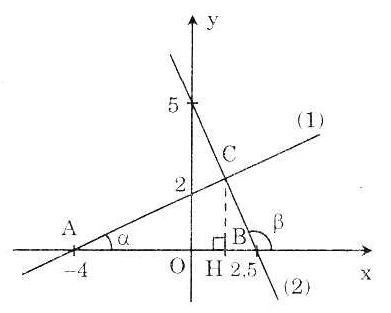c) Ta có AB = 6,5.
Kẻ CH ⊥ AB. Dễ thấy OH = 1,2 ⇒ HB = 1,3
                                                       HA = 5,2
AC² = AH² + CH² = (5,2)² + (2,6)² = 27,04 + 6,67 = 33,8
⇒ AC = 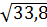 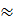  5,81.
Tương tự ta tính được BC 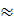 2,91.

d) Ta có: tgα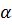  = 0,5  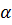⇒   = 26°33’
Tương tự ta tính được 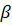 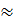 116°34’

Bài 6. a) Vẽ đồ thị các hàm số sau trên cùng một mặt phẳng toa độ:
y = 2x (1);                 y = 0,5x (2);            y = -x + 6 (3)
b) Gọi các giao điểm của đường thẳng có phương trình (3) với hai đường thẳng có phương trình (1) và (2) theo thứ tự là A và B.
Tìm tọa độ của hai điểm A và B.
Tính các góc của tam giác OAB.

Giải:

a) Đồ thị


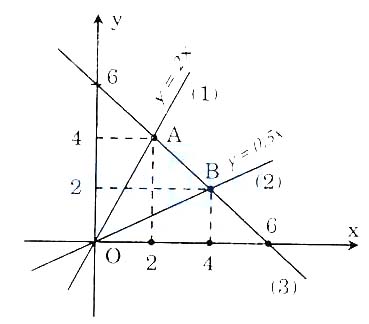b) Hoành độ điểm A là nghiệm của phương trình: 2x = -x + 6. Từ đó ta tính được: A(2; 4).
Hoành độ điểm B là nghiệm của phương trình: 0,5x = -x + 6.
Từ đó ta tính được: B(4; 2).

c) Ta có: OA² = 4² + 2² = 20 ⇒ OA =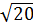
OB² = 2² + 4² = 20 ⇒ OB =
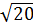OA = OB ⇒ AOB cân, đỉnh O.
Ta lại có: tgBOx = 2 ⇒ 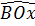 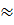  26°33’
tgAOx = 2 ⇒ 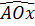 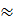   26°26’.
Vậy: 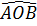   = 63^o26’ - 26°33’ = 36°53’
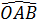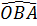   =    =  ( 180° - 36°53’) = 71°33