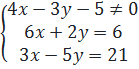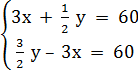Giải bài tập Toán 9: Ôn tập chương III
2019-08-22T22:53:45-04:00
2019-08-22T22:53:45-04:00
Giải bài tập Toán 9: Ôn tập chương III: Tóm tắt kiến thức, ví dụ, hướng dẫn giải bài tập trong sách giáo khoa và bài tập luyện thêm.
/themes/cafe/images/no_image.gif
Bài Kiểm Tra
https://baikiemtra.com/uploads/bai-kiem-tra-logo.png
Thứ năm - 22/08/2019 22:51
Giải bài tập Toán 9: Ôn tập chương III: Tóm tắt kiến thức, ví dụ, hướng dẫn giải bài tập trong sách giáo khoa và bài tập luyện thêm.
A. Tóm tắt kiến thức
Đọc bảng tóm tắt kiến thức cần nhớ và trả lời các câu hỏi trong phần ôn tập chương III, SGK, tr. 25, 26.
B. Ví dụ
Ví dụ 1. Với mỗi phương trình sau hãy tìm ba nghiệm của nó :
a) 5x - 2y = 7 ; b)  x +
x +  y = 2
Giải: a) Từ 5x - 2y = 7 suy ra y =
y = 2
Giải: a) Từ 5x - 2y = 7 suy ra y = 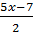 . Với mỗi giá trị của x ta có một giá trị tương ứng của y. Mỗi cặp giá trị tương ứng (x ; y) là một nghiệm của phương trình.
Chẳng hạn:
Với x = -1, ta có y =
. Với mỗi giá trị của x ta có một giá trị tương ứng của y. Mỗi cặp giá trị tương ứng (x ; y) là một nghiệm của phương trình.
Chẳng hạn:
Với x = -1, ta có y = 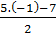 =
= 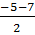 = - 6. Vậy (x ; y) = (-1; -6) là một nghiệm của phương trình.
Với x = 0, ta có y = -
= - 6. Vậy (x ; y) = (-1; -6) là một nghiệm của phương trình.
Với x = 0, ta có y = -  . Vậy (x; y) =
. Vậy (x; y) = 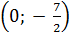 ; là một nghiệm của phương trình.
Với x =
; là một nghiệm của phương trình.
Với x =  , ta có y =
, ta có y = 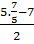 = 0. Vây (x ; y) =
= 0. Vây (x ; y) = 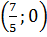 là một nghiệm của phương trình.
b) Từ
là một nghiệm của phương trình.
b) Từ  x +
x +  y = 2 suy ra 4x + 3y = 10. Do đó y =
y = 2 suy ra 4x + 3y = 10. Do đó y = 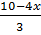 Cho x lần lượt các giá trị x = -1, x = 0, x = 1 ta tìm được các giá trị tương ứng
của y là: y =
Cho x lần lượt các giá trị x = -1, x = 0, x = 1 ta tìm được các giá trị tương ứng
của y là: y = 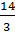 , y=
, y= 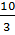 , y = 2.
Vậy ba cặp số
, y = 2.
Vậy ba cặp số 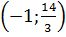 ,
, 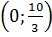 , (1 ; 2) là ba nghiệm của phương trình.
Ví dụ 2. Cho hệ phương trình
, (1 ; 2) là ba nghiệm của phương trình.
Ví dụ 2. Cho hệ phương trình 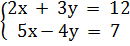 a) Chứng tỏ rằng (3 ; 2) là một nghiệm của hệ phương trình.
b) Minh hoạ hình học tập nghiệm của hệ phương trình.
Giải. Thay x = 3, y = 2 vào hai phương trình ta được :
2.3+ 3.2 = 6+ 6= 12;
5.3-4.2= 15-8 = 7.
Vậy (3 ; 2) là một nghiệm của hệ phương trình.
a) Chứng tỏ rằng (3 ; 2) là một nghiệm của hệ phương trình.
b) Minh hoạ hình học tập nghiệm của hệ phương trình.
Giải. Thay x = 3, y = 2 vào hai phương trình ta được :
2.3+ 3.2 = 6+ 6= 12;
5.3-4.2= 15-8 = 7.
Vậy (3 ; 2) là một nghiệm của hệ phương trình.
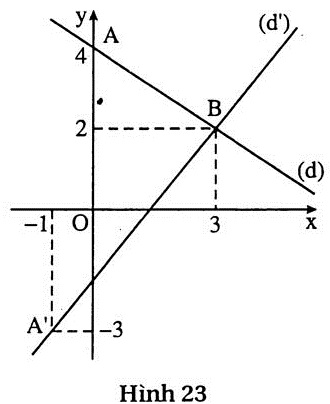
b) (h.23) Vẽ đường thẳng (d): 2x + 3y = 12.
Với x = 0 thì y = 4.
Với x = 3 thì y = 2.
Vậy (d) đi qua A(0 ; 4) và B(3 ; 2).
+ Vẽ đường thẳng (d’) : 5x - 4y = 7.
Với x = -1 thìy = -3.
Với x = 3 thì y = 2.
Vậy (d’) đi qua A’(-1; -3) và B (3; 2) |
|
Ví dụ 3. Giải hệ phương trình : 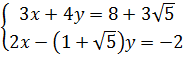 Giải.
Giải.
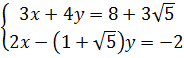 ⇔
⇔ 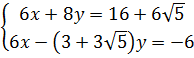 ⇔
⇔ 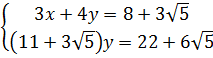 ⇔
⇔ 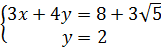 ⇔
⇔ 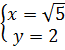 Ví dụ 4. Tìm hàm số bậc nhất biết rằng đồ thị của nó đi qua hai điểm A(4 ; -1), B(-2; 5).
Giải. Giả sử hàm số cần tìm là y = ax + b. Vì đồ thị của nó đi qua A(4 ; -1), B(-2; 5) nên
Ví dụ 4. Tìm hàm số bậc nhất biết rằng đồ thị của nó đi qua hai điểm A(4 ; -1), B(-2; 5).
Giải. Giả sử hàm số cần tìm là y = ax + b. Vì đồ thị của nó đi qua A(4 ; -1), B(-2; 5) nên
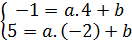 hay
hay 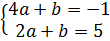 (I)
Giải hệ phương trình (I) với hai ẩn là a và b.
(I) ⇔
(I)
Giải hệ phương trình (I) với hai ẩn là a và b.
(I) ⇔ 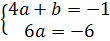 ⇔
⇔ 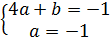 ⇔
⇔ 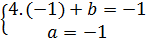 ⇔
⇔ 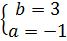 Vậy hàm số cần tìm là y = -x + 3.
C. Hướng dẫn giải bài tập trong sách giáo khoa
40. Giải, a)
Vậy hàm số cần tìm là y = -x + 3.
C. Hướng dẫn giải bài tập trong sách giáo khoa
40. Giải, a) 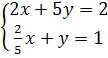 ⇔
⇔ 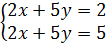 Vì
Vì  =
= 
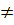
 nên hệ phương trình vô nghiệm.
nên hệ phương trình vô nghiệm.
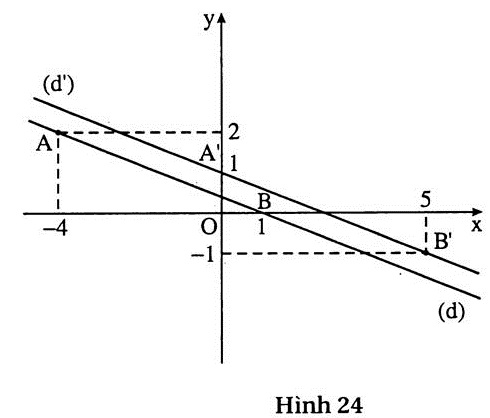
(h.24) Vẽ đường thẳng (d): 2x + 5y = 2.
Với x = - 4 thì y = 2.
Với y = 0 thì x = 1.
Đường thẳng (d) đi qua A(-4 ; 2), B(1 ; 0).
+ Vẽ đường thẳng (d’):  x + y = 1. x + y = 1.
Với x = 0 thì y = 1.
Với x = 5 thì y = -1.
Đường thẳng (d’) đi qua A’(0 ; 1), B’(5 ; -1). |
|
b) 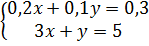 ⇔
⇔ 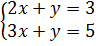 ⇔
⇔ 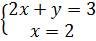 ⇔
⇔ 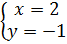
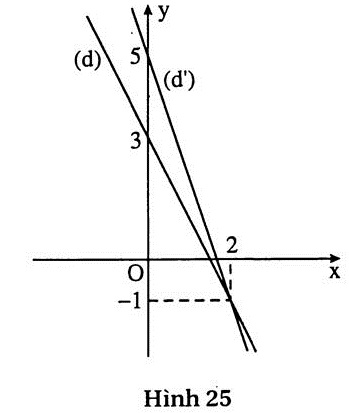
+ (h.25) Vẽ đường thẳng (d): 2x + y = 3.
Với x = 0 thì y = 3.
Với x = 2 thì y = -1.
+ Vẽ đường thẳng (d’): 3x + y = 5.
Với x = 0 thì y = 5.
Với x = 2 thì y = -1. |
|
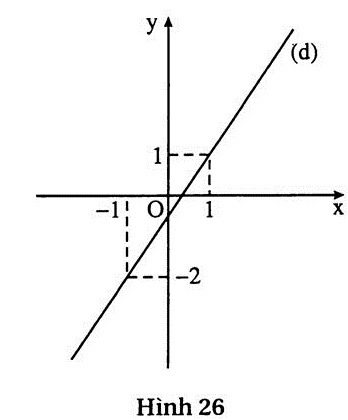
c) 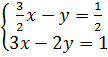 ⇔ ⇔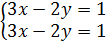
Hệ có vô số nghiệm (h.26).
Tập nghiệm của hệ phương trình là đường thẳng (d): 3x - 2y = 1.
Với x = 1 thì y = 1.
Với x = -1 thì y = -2. |
|
41. Giải, a) 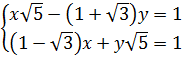 ⇔
⇔ 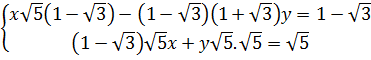 ⇔
⇔ 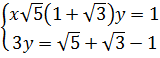 ⇔
⇔ 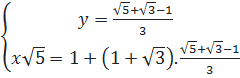 ⇔
⇔ 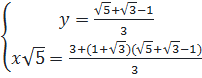 ⇔
⇔ 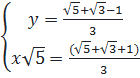 b) Đặt ẩn phụ : u =
b) Đặt ẩn phụ : u = 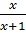 ; v =
; v = 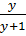 , ta có hệ phương trình
(I)
, ta có hệ phương trình
(I) 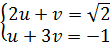 Giải hệ (I) ta được u =
Giải hệ (I) ta được u = 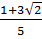 , v =
, v = 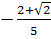 Do đó:
Do đó: 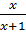 =
= 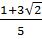 ;
; 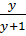 =
= 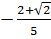 hay 5x = (1 + 3
hay 5x = (1 + 3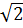 )x + 1 + 3
)x + 1 + 3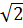 , 5y = -(2 +
, 5y = -(2 + 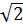 )y - (2 +
)y - (2 + 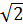 ).
Suy ra x =
).
Suy ra x = 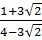 = -
= - 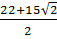 ; y =
; y = 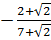 =
= 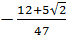 42. Trả lời
a) Vô nghiệm.
b) Vô số nghiệm.
c) (x ; y) =
42. Trả lời
a) Vô nghiệm.
b) Vô số nghiệm.
c) (x ; y) = 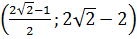 43. Hướng dẫn : Hai người gặp nhau cách A là 2km có nghĩa là người đi từ A đã đi được 2km, người đi từ B đã đi 1,6km và thời gian hai người đi bằng nhau.
Khi một người xuất phát trước 6 phút, họ gặp nhau ở chính giữa quãng đường có nghĩa là hai người đã đi 1,8km và thời gian người đi từ B nhiều hơn thời gian người đi từ A là 6 phút.
Trả lời : 3,6km/h và 4,5km/h.
44. Giải. Gọi khối lượng đồng trong 124g hợp kim là x (gam), khối lượng kẽm là y (gam);
43. Hướng dẫn : Hai người gặp nhau cách A là 2km có nghĩa là người đi từ A đã đi được 2km, người đi từ B đã đi 1,6km và thời gian hai người đi bằng nhau.
Khi một người xuất phát trước 6 phút, họ gặp nhau ở chính giữa quãng đường có nghĩa là hai người đã đi 1,8km và thời gian người đi từ B nhiều hơn thời gian người đi từ A là 6 phút.
Trả lời : 3,6km/h và 4,5km/h.
44. Giải. Gọi khối lượng đồng trong 124g hợp kim là x (gam), khối lượng kẽm là y (gam);
x > 0, y > 0. Ta có phương trình x + y = 124. (1)
Vì 89g đồng có thể tích 10cm3, 7g kẽm có thể tích 1cm3 nên mỗi gam đồng có thể tích 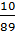 cm3, mỗi gam kẽm có thể tích
cm3, mỗi gam kẽm có thể tích  cm3.
Do đó trong miếng hợp kim này đồng có thể tích là
cm3.
Do đó trong miếng hợp kim này đồng có thể tích là 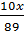 cm3, kẽm có thể tích là
cm3, kẽm có thể tích là  cm3 .
Ta có phương trình :
cm3 .
Ta có phương trình : 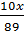 +
+  = 15 hay 70x + 89y = 9345. (2)
Giải hệ phương trình:
= 15 hay 70x + 89y = 9345. (2)
Giải hệ phương trình: 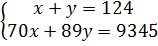 Ta được (x ; y) = (89 ; 35).
Trả lời: 89g đồng và 35g kẽm.
45. Giải. Gọi thời gian đội I làm một mình xong việc là x (ngày),
Thời gian đội II làm một mình xong việc là y (ngày).
Mỗi ngày đội I làm được
Ta được (x ; y) = (89 ; 35).
Trả lời: 89g đồng và 35g kẽm.
45. Giải. Gọi thời gian đội I làm một mình xong việc là x (ngày),
Thời gian đội II làm một mình xong việc là y (ngày).
Mỗi ngày đội I làm được  (công việc);
đội II làm được
(công việc);
đội II làm được  (công việc)
Khi làm chung mỗi ngày hai đội làm được
(công việc)
Khi làm chung mỗi ngày hai đội làm được 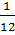 (công việc).
Do đó có phương trình :
(công việc).
Do đó có phương trình :  +
+  =
= 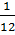 .
Hai đội làm chung 8 ngày được :
.
Hai đội làm chung 8 ngày được : 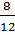 hay
hay  (công việc).
Đội II làm tiếp với năng suất cải tiến, mỗi ngày làm được
(công việc).
Đội II làm tiếp với năng suất cải tiến, mỗi ngày làm được  (công việc) nên họ chỉ làm trong 3,5 ngày nữa là xong việc. Do đó :
(công việc) nên họ chỉ làm trong 3,5 ngày nữa là xong việc. Do đó :
 +
+ 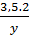 = 1 hay
= 1 hay  +
+  = 1.
Giải hệ phương trình:
= 1.
Giải hệ phương trình: 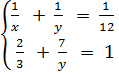 Ta được : (x ; y) = (28 ; 21).
Trả lời : Đội I làm một mình 28 ngày thì xong việc.
Đội II làm một mình 21 ngày thì xong việc.
46. Trả lời: Năm ngoái, đơn vị thứ nhất thu được 420 tấn ;
đơn vị thứ hai thu được 300 tấn.
Năm nay, đơn vị thứ nhất thu được 483 tấn ;
đơn vị thứ hai thu được 336 tấn.
D. Bài tập luyện thêm.
1. Giải các hệ phương trình :
a)
Ta được : (x ; y) = (28 ; 21).
Trả lời : Đội I làm một mình 28 ngày thì xong việc.
Đội II làm một mình 21 ngày thì xong việc.
46. Trả lời: Năm ngoái, đơn vị thứ nhất thu được 420 tấn ;
đơn vị thứ hai thu được 300 tấn.
Năm nay, đơn vị thứ nhất thu được 483 tấn ;
đơn vị thứ hai thu được 336 tấn.
D. Bài tập luyện thêm.
1. Giải các hệ phương trình :
a) 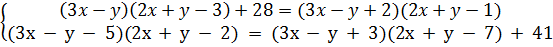 b)
b) 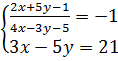 2. Tìm giá trị của a và b để đồ thị y = ax + b đi qua điểm M(-2 ; 4) và giao điểm của hai đường thẳng (d): x - 5y = 8 và (d’): 3x + 2y = 7.
3. Trên một con đường, thị trấn A nằm giữa hai thị trấn B và C. Một người đi xe đạp khởi hành từ A đến B. Sau đó 2 giờ 30 phút một người đi xe máy khởi hành từ B đi về phía A và nửa giờ sau thì gặp người đi xe đạp. Một lần khác, người đi xe đạp khởi hành từ A để đến C ; sau đó 1 giờ 30 phút người đi xe máy khởi hành từ B đuổi theo và đi được 1 giờ 30 phút thì đuổi kịp người đi xe đạp. Tính vận tốc của mỗi người, biết rằng khoảng cách giữa A và B là 60km, và trong cả hai lần vận tốc của mỗi người không thay đổi.
4. Để sửa chữa một ngôi nhà cần một số công nhân và làm trong một thời gian quy định. Nếu giảm đi 3 công nhân thì cần thêm 9 ngày mới xong việc. Nếu tăng thêm 4 công nhân thì làm xong việc sớm 6 ngày. Hỏi theo dự định cần bao nhiêu công nhân và bao nhiêu ngày ?
Hướng dẫn - Đáp số
1. a) Hướng dẫn : Đặt ẩn phụ : u = 3x - y ; v = 2x + y.
Đáp số: (x ; y) = (3 ; -1).
b) Giải:
2. Tìm giá trị của a và b để đồ thị y = ax + b đi qua điểm M(-2 ; 4) và giao điểm của hai đường thẳng (d): x - 5y = 8 và (d’): 3x + 2y = 7.
3. Trên một con đường, thị trấn A nằm giữa hai thị trấn B và C. Một người đi xe đạp khởi hành từ A đến B. Sau đó 2 giờ 30 phút một người đi xe máy khởi hành từ B đi về phía A và nửa giờ sau thì gặp người đi xe đạp. Một lần khác, người đi xe đạp khởi hành từ A để đến C ; sau đó 1 giờ 30 phút người đi xe máy khởi hành từ B đuổi theo và đi được 1 giờ 30 phút thì đuổi kịp người đi xe đạp. Tính vận tốc của mỗi người, biết rằng khoảng cách giữa A và B là 60km, và trong cả hai lần vận tốc của mỗi người không thay đổi.
4. Để sửa chữa một ngôi nhà cần một số công nhân và làm trong một thời gian quy định. Nếu giảm đi 3 công nhân thì cần thêm 9 ngày mới xong việc. Nếu tăng thêm 4 công nhân thì làm xong việc sớm 6 ngày. Hỏi theo dự định cần bao nhiêu công nhân và bao nhiêu ngày ?
Hướng dẫn - Đáp số
1. a) Hướng dẫn : Đặt ẩn phụ : u = 3x - y ; v = 2x + y.
Đáp số: (x ; y) = (3 ; -1).
b) Giải: 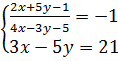 ⇔
⇔ 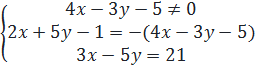 ⇔
⇔ 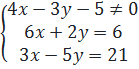 Giải hệ này ta được : (x ; y) = (2 ; -3).
Với x = 2, y = - 3 thì 4x - 3y - 5 = 4. 2 - 3. (-3) -5=12
Giải hệ này ta được : (x ; y) = (2 ; -3).
Với x = 2, y = - 3 thì 4x - 3y - 5 = 4. 2 - 3. (-3) -5=12 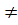 0.
Vậy hệ có nghiệm duy nhất là (x ; y) = (2 ; -3).
2. Hướng dẫn : Tìm giao điểm của (d) và (d’).
Trả lời: y = - x + 2.
3. Giải. Gọi vận tốc người đi xe đạp là x (km/h), vận tốc người đi xe máy là y (km/h),
0.
Vậy hệ có nghiệm duy nhất là (x ; y) = (2 ; -3).
2. Hướng dẫn : Tìm giao điểm của (d) và (d’).
Trả lời: y = - x + 2.
3. Giải. Gọi vận tốc người đi xe đạp là x (km/h), vận tốc người đi xe máy là y (km/h),
x > 0, y > 0.
Vì người đi xe máy khởi hành sau người đi xe đạp là 2 giờ 30 phút nên đến khi gặp nhau thì người đi xe đạp đã đi 3 giờ. Do đó có phương trình 3x +  y = 60.
Vì người đi xe đạp đi trước người đi xe máy 1 giờ 30 phút nên đến lúc gặp nhau người đi xe đạp đã đi 3 giờ. Hơn nữa, đến khi gặp nhau, quãng đường người đi xe máy đã đi dài hơn quãng đường của người đi xe đạp là 60km. Do đó có phương trình :
y = 60.
Vì người đi xe đạp đi trước người đi xe máy 1 giờ 30 phút nên đến lúc gặp nhau người đi xe đạp đã đi 3 giờ. Hơn nữa, đến khi gặp nhau, quãng đường người đi xe máy đã đi dài hơn quãng đường của người đi xe đạp là 60km. Do đó có phương trình :  y – 3x = 60
Giải hệ phương trình:
y – 3x = 60
Giải hệ phương trình: 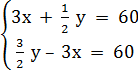 Ta được : (x ; y) = (10 ; 60).
Trả lời: Vận tốc của người đi xe đạp là 10km/h.
Vận tốc của người đi xe máy là 60km/h.
4. Giải. Gọi số công nhân theo dự định là x (người) và số thời gian dự định là y (ngày),
Ta được : (x ; y) = (10 ; 60).
Trả lời: Vận tốc của người đi xe đạp là 10km/h.
Vận tốc của người đi xe máy là 60km/h.
4. Giải. Gọi số công nhân theo dự định là x (người) và số thời gian dự định là y (ngày),
x > 0, y > 0, x 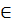 N*.
Coi toàn bộ công việc là 1 đơn vị.
Thế thì x công nhân làm việc trong 1 ngày được
N*.
Coi toàn bộ công việc là 1 đơn vị.
Thế thì x công nhân làm việc trong 1 ngày được  (công việc).
Do đó một công nhân làm việc trong 1 ngày được
(công việc).
Do đó một công nhân làm việc trong 1 ngày được  (công việc).
Nếu giảm 3 công nhân và tăng 9 ngày thì khối lượng công việc làm được là:
(x - 3)(y + 9).
(công việc).
Nếu giảm 3 công nhân và tăng 9 ngày thì khối lượng công việc làm được là:
(x - 3)(y + 9). (công việc) hay
(công việc) hay 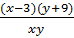 Vì khi đó hoàn thành toàn bộ công việc nên ta có phương trình :
Vì khi đó hoàn thành toàn bộ công việc nên ta có phương trình :
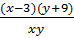 = 1 hay (x - 3)(y + 9) = xy
Tương tự, nếu tăng 4 công nhân và xong sớm 6 ngày thì ta có phương trình :
= 1 hay (x - 3)(y + 9) = xy
Tương tự, nếu tăng 4 công nhân và xong sớm 6 ngày thì ta có phương trình :
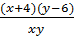 = 1 hay (x + 4)(y - 6) = xy
Giải hệ phương trình:
= 1 hay (x + 4)(y - 6) = xy
Giải hệ phương trình: 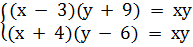 Ta được (x ; y) = (10 ; 21).
Trả lời : Theo dự định cần : 10 công nhân, và thời gian hoàn thành công việc trong 21 ngày.
Ta được (x ; y) = (10 ; 21).
Trả lời : Theo dự định cần : 10 công nhân, và thời gian hoàn thành công việc trong 21 ngày.
© Bản quyền thuộc về
Bài kiểm tra. Ghi rõ nguồn Bài kiểm tra.com khi sao chép nội dung này.
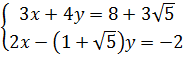
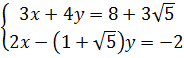 ⇔
⇔ 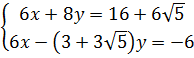
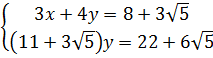 ⇔
⇔ 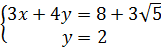 ⇔
⇔ 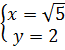
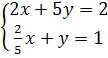 ⇔
⇔ 
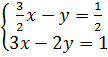 ⇔
⇔
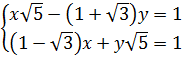
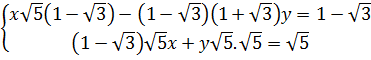
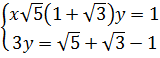 ⇔
⇔ 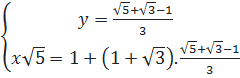
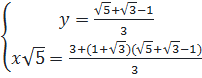 ⇔
⇔ 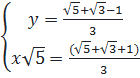
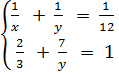
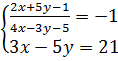
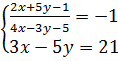 ⇔
⇔ 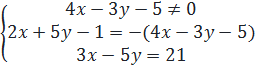 ⇔
⇔