Giải bài tập Toán 9: Ôn tập chương IV
2019-08-27T04:48:05-04:00
2019-08-27T04:48:05-04:00
Giải bài tập Toán 9: Ôn tập chương IV : Tóm tắt kiến thức, ví dụ, hướng dẫn giải bài tập trong sách giáo khoa và bài tập luyện thêm.
/themes/cafe/images/no_image.gif
Bài Kiểm Tra
https://baikiemtra.com/uploads/bai-kiem-tra-logo.png
Thứ ba - 27/08/2019 04:39
Giải bài tập Toán 9: Ôn tập chương IV : Tóm tắt kiến thức, ví dụ, hướng dẫn giải bài tập trong sách giáo khoa và bài tập luyện thêm.
A. Tóm tắt kiến thức
Trả lời các câu hỏi và học thuộc phần tóm tắt các kiến thức cần nhớ ở các trang 60-62, SGK.
B. Ví dụ
Ví dụ 1. Cho các hàm số y = 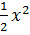 , y =
, y = 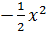 , y = x.
a) Vẽ các đồ thị của ba hàm số trên cùng một mặt phẳng toạ độ.
b) Tìm các giao điểm của các đồ thị.
Giải:
, y = x.
a) Vẽ các đồ thị của ba hàm số trên cùng một mặt phẳng toạ độ.
b) Tìm các giao điểm của các đồ thị.
Giải:
| x |
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
| y = x |
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
y = 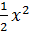 |
 |
2 |
 |
0 |
 |
2 |
 |
y = 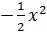 |
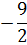 |
-2 |
 |
0 |
 |
-2 |
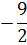 |
Giao điểm của cả ba đồ thị là O(0 ; 0) (h.38).
Giao điểm của hai đồ thị y = 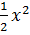 và y = x là O và M(2 ; 2). và y = x là O và M(2 ; 2).
Giao điểm của hai đồ thị y = 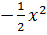 và y = x là O và M’(-2 ; -2). và y = x là O và M’(-2 ; -2). |
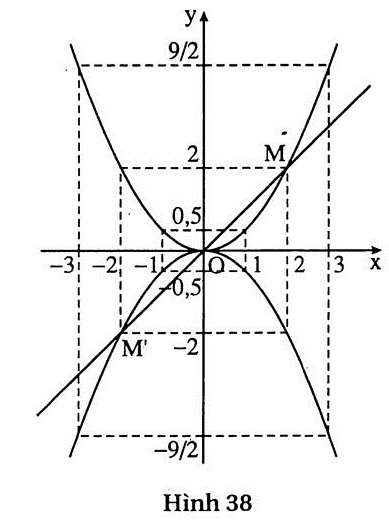 |
Ví dụ 2. Tìm các giá trị của m để phương trình mx2 - 4(m + 2)x + 4m -1 = 0.
a) Có nghiệm.
b) Có hai nghiệm phân biệt.
c) Có nghiệm kép.
d) Vô nghiệm.
Giải: a) Khi m = 0 thì phương trình đã cho trở thành -8x -1=0.
Nó có nghiệm x = 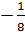 Khi m
Khi m 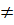 0, '
0, '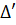 = 4(m2 + 4m + 4) - m(4m -1) = 4m2 + 16m + 16 - 4m2 + m = 17m + 16.
Phương trình có nghiệm khi 17m + 16
= 4(m2 + 4m + 4) - m(4m -1) = 4m2 + 16m + 16 - 4m2 + m = 17m + 16.
Phương trình có nghiệm khi 17m + 16 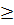 0 hay khi m
0 hay khi m 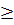
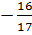 Vì m = 0 cũng thoả mãn điều kiện m
Vì m = 0 cũng thoả mãn điều kiện m 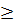
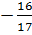 nên ta có kết luận chung :
Phương trình có nghiệm khi m
nên ta có kết luận chung :
Phương trình có nghiệm khi m 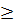
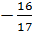 b) Phương trình có hai nghiệm phân biệt khi m >
b) Phương trình có hai nghiệm phân biệt khi m > 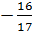 và m
và m 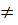 0.
c) Phương trình có nghiệm kép khi m =
0.
c) Phương trình có nghiệm kép khi m = 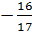 d) Phương trình vô nghiệm khi m <
d) Phương trình vô nghiệm khi m < 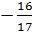 Ví dụ 3. Giải các phương trình :
a) 5x4 - 2x2 - 3 = 2x2 + 6 ;
b) (x2 - 5x)2 - 3x2 + 15x + 2 = 0.
Giải: a) 5x4 - 2x2 - 3 = 2x2 + 6 ⇔ 5x4 - 4x2 - 9 = 0.
Đặt t = x2, t
Ví dụ 3. Giải các phương trình :
a) 5x4 - 2x2 - 3 = 2x2 + 6 ;
b) (x2 - 5x)2 - 3x2 + 15x + 2 = 0.
Giải: a) 5x4 - 2x2 - 3 = 2x2 + 6 ⇔ 5x4 - 4x2 - 9 = 0.
Đặt t = x2, t 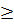 0, ta được : 5t2 - 4t - 9 = 0. (*)
Vì 5 - (-4) + (-9) = 0 nên phương trình (*) có nghiệm : t1 = -1 (loại), t2 =
0, ta được : 5t2 - 4t - 9 = 0. (*)
Vì 5 - (-4) + (-9) = 0 nên phương trình (*) có nghiệm : t1 = -1 (loại), t2 =  .
Với t =
.
Với t =  , ta có x2 =
, ta có x2 =  . Do đó x =
. Do đó x = 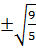 =
= 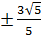 Vậy phương trình đã cho có hai nghiệm : x =
Vậy phương trình đã cho có hai nghiệm : x = 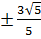 b) Phân tích. Nhận thấy -3x2 + 15x = -3(x2 - 5x) nên có thể đặt ẩn phụ t = x2 - 5x.
Đặt t = x2 - 5x, phương trình đã cho trở thành : t2 - 3t + 2 = 0. (*)
Vì 1 - 3 + 2 = 0 nên phương trình (*) có hai nghiệm là : t1 = 1, t2 = 2.
Với t = 1, ta có x2 - 5x = 1 hay x2 - 5x - 1 = 0.
Ta có:
b) Phân tích. Nhận thấy -3x2 + 15x = -3(x2 - 5x) nên có thể đặt ẩn phụ t = x2 - 5x.
Đặt t = x2 - 5x, phương trình đã cho trở thành : t2 - 3t + 2 = 0. (*)
Vì 1 - 3 + 2 = 0 nên phương trình (*) có hai nghiệm là : t1 = 1, t2 = 2.
Với t = 1, ta có x2 - 5x = 1 hay x2 - 5x - 1 = 0.
Ta có:  = 25 - 4.(-1) = 29.
Vậy x1 =
= 25 - 4.(-1) = 29.
Vậy x1 = 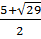 ; x2 =
; x2 = 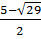 Với t = 2, ta có x2 - 5x = 2 hay x2 - 5x - 2 = 0.
Ta có:
Với t = 2, ta có x2 - 5x = 2 hay x2 - 5x - 2 = 0.
Ta có:  = 25 - 4.(-2) = 33
Vậy: x3 =
= 25 - 4.(-2) = 33
Vậy: x3 =  ; x4 =
; x4 = 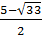 Phương trình đã cho có 4 nghiệm:
x1 =
Phương trình đã cho có 4 nghiệm:
x1 = 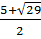 ; x2 =
; x2 = 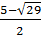 ; x3 =
; x3 = 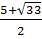 ; x4 =
; x4 = 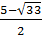 C. Hướng dẫn giải bài tập trong sách giáo khoa
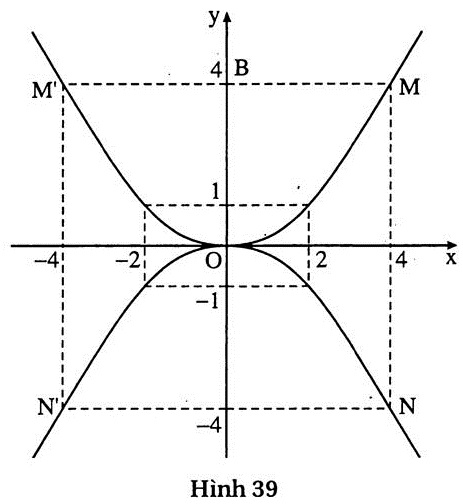
54. Giải: (h.39)
C. Hướng dẫn giải bài tập trong sách giáo khoa
54. Giải: (h.39)
| x |
-4 |
-2 |
0 |
2 |
4 |
y =  x2 x2 |
4 |
1 |
0 |
1 |
4 |
y = 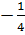 x2 x2 |
-4 |
-1 |
0 |
-1 |
-4 |
a) Hoành độ của M là 4, của M’ là -4.
b) Đường thẳng NN’ // MM’. Vì tung độ của N và N’ lần lượt là số đối của tung độ của M và M’. Do đó tung độ của N và N’ bằng nhau.
- Trên hình vẽ ta nhận thấy tung độ của N và N’ đều bằng -4.
- Vì hoành độ của N là 4 nên tung độ của N là y = 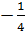 .42 = - 4. .42 = - 4.
Hoành độ của N’ là -4 nên tung độ của N’ là y = .(- 4)2 = - 4. .(- 4)2 = - 4. |
 |
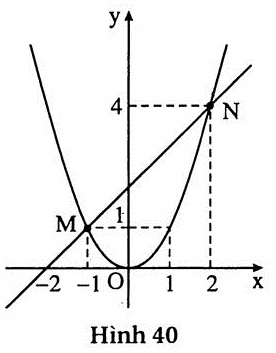
55. Giải: (h.40) a) Phương trình x2 - x - 2 = 0 có 1 - (-1) -2 = 0 nên có hai nghiệm là x1 = -1 và x2 = 2.
b), c) Trên hình vẽ ta nhận thấy nghiệm x1 = -1 và nghiệm x2 = 2 lần lượt là hoành độ của hai giao điểm M và N. |
 |
56. Giải. a) 3x4 - 12x2 + 9 = 0. Đặt t = x2 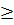 0, ta có : 3t2 - 12t + 9 = 0 hay t - 4t + 3 = 0. Phương trình thoả mãn điều kiện a + b + c = 0 nên có hai nghiệm t1 = 1, t2 = 3.
Vậy x1 = 1, x2 = -1, x3 =
0, ta có : 3t2 - 12t + 9 = 0 hay t - 4t + 3 = 0. Phương trình thoả mãn điều kiện a + b + c = 0 nên có hai nghiệm t1 = 1, t2 = 3.
Vậy x1 = 1, x2 = -1, x3 = 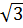 , x4 =
, x4 = 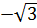 .
b) 2x4 + 3x2 - 2 = 0. Đặt t = x2
.
b) 2x4 + 3x2 - 2 = 0. Đặt t = x2 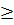 0, ta có : 2t2 + 3t - 2 = 0.
0, ta có : 2t2 + 3t - 2 = 0.
 = 9 + 16 = 25,
= 9 + 16 = 25, 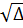 = 5; Ta có: t1 =
= 5; Ta có: t1 = 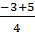 =
=  ; t2 = -2 (loại)
Vậy: x1 =
; t2 = -2 (loại)
Vậy: x1 = 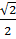 ; x2 =
; x2 = 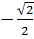 c) x4 + 5x2 +1= 0. Đặt t = x2
c) x4 + 5x2 +1= 0. Đặt t = x2 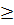 0, ta có : t2 + 5t + 1 = 0.
0, ta có : t2 + 5t + 1 = 0.  = 25 - 4 = 21.
Vậy t1 =
= 25 - 4 = 21.
Vậy t1 = 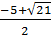 < 0 (loại), t2 =
< 0 (loại), t2 = 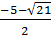 < 0 (loại)
Phương trình vô nghiệm.
57. Giải. a) 5x2 - 3x + 1 = 2x + 11 ⇔ 5x2 - 5x - 10 = 0 ⇔ x2 - x - 2 = 0.
Phương trình thoả mãn điều kiện a - b + c = 1 + 1 - 2 = 0 nên có hai nghiệm :
x1 = - 1, x2 = 2.
b)
< 0 (loại)
Phương trình vô nghiệm.
57. Giải. a) 5x2 - 3x + 1 = 2x + 11 ⇔ 5x2 - 5x - 10 = 0 ⇔ x2 - x - 2 = 0.
Phương trình thoả mãn điều kiện a - b + c = 1 + 1 - 2 = 0 nên có hai nghiệm :
x1 = - 1, x2 = 2.
b) 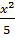 -
- 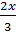 =
= 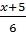 ⇔ 6x2 - 20x = 5x + 25 ⇔ 6x2 – 25x – 25 = 0
Ta có :
⇔ 6x2 - 20x = 5x + 25 ⇔ 6x2 – 25x – 25 = 0
Ta có :  = 252 + 4.6.25 = 25(25 + 24) = 25.49,
= 252 + 4.6.25 = 25(25 + 24) = 25.49, 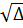 = 35.
Vậy x1 =5, x2 =
= 35.
Vậy x1 =5, x2 = 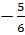 c) Điều kiện : x
c) Điều kiện : x 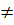 0, x
0, x 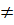 2.
2.
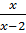 =
= 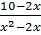 ⇔ x2 = 10 - 2x ⇔ x2 + 2x – 10 = 0. '
⇔ x2 = 10 - 2x ⇔ x2 + 2x – 10 = 0. '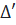 = 1 + 10 = 11
Vậy: x1 = -1 +
= 1 + 10 = 11
Vậy: x1 = -1 + 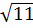 , x2 = -1 -
, x2 = -1 - 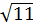 Cả hai giá trị này đều thoả mãn điều kiện của ẩn. Vậy phương trình có hai nghiệm là :
Cả hai giá trị này đều thoả mãn điều kiện của ẩn. Vậy phương trình có hai nghiệm là :
x1 = -1 + 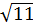 , x2 = -1 -
, x2 = -1 - 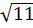 d) Điều kiện : x
d) Điều kiện : x 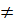
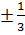
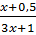 =
= 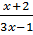 -
- 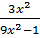 ⇔
⇔ 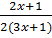 =
= 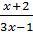 -
- 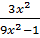 ⇔ (2x + 1 )(3x - 1) = 2(x + 2)(3x + 1) - 2.3x2
⇔ 6x2 + x - 1 = 6x2 + 14x + 4 - 6x2
⇔ 6x2 - 13x - 5 = 0.
Ta có :
⇔ (2x + 1 )(3x - 1) = 2(x + 2)(3x + 1) - 2.3x2
⇔ 6x2 + x - 1 = 6x2 + 14x + 4 - 6x2
⇔ 6x2 - 13x - 5 = 0.
Ta có :  = 169 + 120 = 289,
= 169 + 120 = 289, 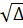 = 17 .
Vậy x1 =
= 17 .
Vậy x1 =  , x2 =
, x2 = 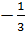 (loại).
Phương trình có một nghiệm : x =
(loại).
Phương trình có một nghiệm : x =  e) 2
e) 2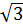 x2 + x + 1 =
x2 + x + 1 = 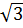 (x + 1) ⇔ 2
(x + 1) ⇔ 2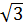 x2 - (
x2 - (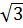 - 1)x + 1 -
- 1)x + 1 - 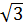 = 0.
= 0.
 = (
= (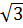 - 1)2 - 8
- 1)2 - 8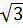 (1 -
(1 - 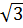 ) = 4 - 2
) = 4 - 2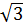 - 8
- 8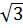 + 24 = 25 - 2.5
+ 24 = 25 - 2.5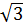 + 3 = (5 -
+ 3 = (5 - 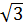 )2 .
Vậy x1 =
)2 .
Vậy x1 = 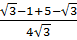 =
= 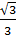 ; x2 =
; x2 = 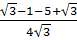 =
= 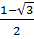 f) x2 +2
f) x2 +2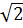 x + 4 = 3(x +
x + 4 = 3(x +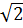 ) ⇔ x2 + (2
) ⇔ x2 + (2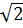 - 3)x + 4 - 3
- 3)x + 4 - 3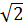 = 0.
Ta có :
= 0.
Ta có :  = 8 - 12
= 8 - 12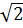 + 9 - 16 + 12
+ 9 - 16 + 12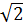 = 1.
Vậy x1 =
= 1.
Vậy x1 = 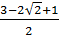 = 2 -
= 2 - 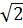 , x2 =
, x2 = 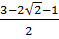 = 1 -
= 1 - 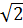 58. Giải. a) 1,2x3 – x2 - 0,2x = 0 ⇔ x(1,2x2 - x - 0,2) = 0
⇔
58. Giải. a) 1,2x3 – x2 - 0,2x = 0 ⇔ x(1,2x2 - x - 0,2) = 0
⇔ 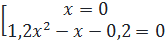 Phương trình có ba nghiệm : x1 = 0, x2 = 1, x3 =
Phương trình có ba nghiệm : x1 = 0, x2 = 1, x3 = 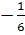 .
b) 5x3 – x2 - 5x + 1 = 0 ⇔ x2(5x - 1) - (5x - 1) = 0 ⇔ (5x - 1)(x2 - 1) = 0
⇔
.
b) 5x3 – x2 - 5x + 1 = 0 ⇔ x2(5x - 1) - (5x - 1) = 0 ⇔ (5x - 1)(x2 - 1) = 0
⇔ 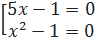 Phương trình có ba nghiệm : x1 =
Phương trình có ba nghiệm : x1 =  , x2 = 1, x3 = -1.
59. Giải: a) 2(x2 - 2x)2 + 3(x2 - 2x) +1=0. Đặt x2 - 2x = t, ta có : 2t2 + 3t + 1 = 0.
Ta có nghiệm t1 = -1, t2 =
, x2 = 1, x3 = -1.
59. Giải: a) 2(x2 - 2x)2 + 3(x2 - 2x) +1=0. Đặt x2 - 2x = t, ta có : 2t2 + 3t + 1 = 0.
Ta có nghiệm t1 = -1, t2 = 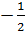 .
- Với t1 = -1, ta có : x2 - 2x = -1 hay x2 - 2x + 1 = 0.
Phương trình có nghiệm kép : x1 = x2 = 1.
- Với t1= -4, ta có : x - 2x =
.
- Với t1 = -1, ta có : x2 - 2x = -1 hay x2 - 2x + 1 = 0.
Phương trình có nghiệm kép : x1 = x2 = 1.
- Với t1= -4, ta có : x - 2x = 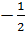 hay 2x2 - 4x + 1 = 0.
Phương trình có hai nghiệm phân biệt: x3 =
hay 2x2 - 4x + 1 = 0.
Phương trình có hai nghiệm phân biệt: x3 = 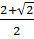 ; x4 =
; x4 = 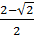 Vậy phương trình có ba nghiệm : x1 = x2 = 1; x3 =
Vậy phương trình có ba nghiệm : x1 = x2 = 1; x3 = 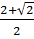 ; x4 =
; x4 = 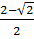 b)
b) 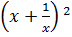 - 4
- 4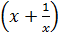 + 3 = 0 Điều kiện : x
+ 3 = 0 Điều kiện : x 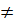 0.
Đặt x +
0.
Đặt x +  = t, ta có : t2 - 4t + 3 = 0 ⇒ t1 = 1, t2 = 3.
- Với t1 = 1, ta có : x +
= t, ta có : t2 - 4t + 3 = 0 ⇒ t1 = 1, t2 = 3.
- Với t1 = 1, ta có : x +  = 1 hay x2 - x + 1 = 0. Phương trình vô nghiệm.
- Với t2 = 3, ta có : x +
= 1 hay x2 - x + 1 = 0. Phương trình vô nghiệm.
- Với t2 = 3, ta có : x +  =3 hay x2 - 3x + 1 = 0. Phương trình có hai nghiệm :
x1 =
=3 hay x2 - 3x + 1 = 0. Phương trình có hai nghiệm :
x1 = 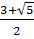 ; x2 =
; x2 = 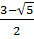 60. Giải: a) Theo hệ thức Vi-ét:
60. Giải: a) Theo hệ thức Vi-ét:  + x2 =
+ x2 = 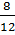 =
=  . Do đó x2 =
. Do đó x2 =  -
-  =
=  b) Theo hệ thức Vi-ét: -3.x2 =
b) Theo hệ thức Vi-ét: -3.x2 = 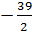 . Do đó x2 =
. Do đó x2 = 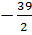 : (-3) =
: (-3) = 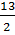 c) Theo hệ thức Vi-ét:
c) Theo hệ thức Vi-ét: 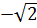 + x2 = -1. Do đó x2 = -1 +
+ x2 = -1. Do đó x2 = -1 + 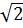 .
d) Vì phương trình có nghiệm là x1 = 2 nên 22 - 2m.2 + m - 1 = 0 hay -3m + 3=0. Suy ra m = 1. Theo hệ thức Vi-ét: 2 + x2 = 2. Do đó x2 = 0.
61. Giải: a) Biết u + v = 12, uv = 28 và u > v.
Ta có : u và v là hai nghiệm của phương trình :
x2 - 12x + 28 = 0. '
.
d) Vì phương trình có nghiệm là x1 = 2 nên 22 - 2m.2 + m - 1 = 0 hay -3m + 3=0. Suy ra m = 1. Theo hệ thức Vi-ét: 2 + x2 = 2. Do đó x2 = 0.
61. Giải: a) Biết u + v = 12, uv = 28 và u > v.
Ta có : u và v là hai nghiệm của phương trình :
x2 - 12x + 28 = 0. ' = 36 - 28 = 8.
Vậy x1 = 6 +2
= 36 - 28 = 8.
Vậy x1 = 6 +2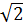 , x2 = 6 - 2
, x2 = 6 - 2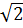 .
Vì 6+ 2
.
Vì 6+ 2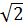 > 6 - 2
> 6 - 2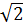 nên u = 6 + 2
nên u = 6 + 2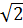 , v = 6 - 2
, v = 6 - 2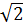 .
b) u + v = 3, uv = 6 ⇒ u và v là hai nghiệm của phương trình : x2 -3x + 6 = 0. Ta có : '
.
b) u + v = 3, uv = 6 ⇒ u và v là hai nghiệm của phương trình : x2 -3x + 6 = 0. Ta có : '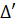 = 6 - 24 = -15 < 0. Phương trình vô nghiệm.
Vậy không có hai số u và v nào thoả mãn các điều kiện đã cho.
62. Giải, a) '
= 6 - 24 = -15 < 0. Phương trình vô nghiệm.
Vậy không có hai số u và v nào thoả mãn các điều kiện đã cho.
62. Giải, a) '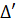 = (m - 1)2 + 7m2 > 0 với mọi giá trị của m. Do đó phương trình có nghiệm với mọi giá trị của m.
b) Gọi x1, x2 là hai nghiệm của phương trình ta có :
= (m - 1)2 + 7m2 > 0 với mọi giá trị của m. Do đó phương trình có nghiệm với mọi giá trị của m.
b) Gọi x1, x2 là hai nghiệm của phương trình ta có :
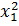 +
+ 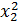 = (x1 + x2)2 - 2x1x2 =
= (x1 + x2)2 - 2x1x2 = 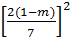 - 2
- 2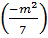 =
= 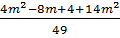 =
= 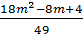 63. Giải. Gọi tỉ số tăng dân số trung bình mỗi năm là x(%), x > 0.
Sau một năm dân số của thành phố là :
2 000 000 + 2 000 000.
63. Giải. Gọi tỉ số tăng dân số trung bình mỗi năm là x(%), x > 0.
Sau một năm dân số của thành phố là :
2 000 000 + 2 000 000. 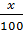 Hay 2 000 000 + 20 000x (người)
Sau hai năm dân số của thành phố là :
2 000 000 + 20 000x + (2 000 000 + 20 000x)
Hay 2 000 000 + 20 000x (người)
Sau hai năm dân số của thành phố là :
2 000 000 + 20 000x + (2 000 000 + 20 000x) 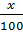 hay 2 000 000 + 40 000x + 200x2 (người).
Theo đầu bài ta có phương trình : 200x2 + 40 000x + 2 000 000 = 2 020 050
hay 2 000 000 + 40 000x + 200x2 (người).
Theo đầu bài ta có phương trình : 200x2 + 40 000x + 2 000 000 = 2 020 050
hay 4x2 + 800x - 401 = 0.
Giải phương trình : '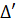 = 160 000 + 1604 =161 604, '
= 160 000 + 1604 =161 604, '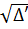 = 402.
⇒ x1 =
= 402.
⇒ x1 = 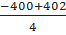 = 0,5; x2 =
= 0,5; x2 = 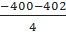 < 0
Vì x > 0 nên x2 không thoả mãn điều kiện của ẩn.
Trả lời : Tỉ số tăng dân số trung bình một năm của thành phố này là 0,5%.
64. Giải. Gọi số mà đầu bài đã cho là x, x dương.
Bạn Quân đã chọn số x - 2 để nhân với x.
Vì tích này là 120 nên ta có phương trình : x(x - 2) = 120 hay x2 - 2x - 120 = 0. Giải phương trình ta được số đã cho là 12.
Nhưng đầu bài yêu cầu tìm tích của x với x + 2. Vậy kết quả đúng phải là:
12.14= 168.
Trả lời : Kết quả đúng phải là 168.
65. Giải. Gọi vận tốc của xe lửa thứ nhất là : x (km/h), x > 0.
Khi đó vận tốc của xe lửa thứ hai là : x + 5 (km/h).
Thời gian xe lửa thứ nhất đi từ Hà Nội đến chỗ gặp nhau là :
< 0
Vì x > 0 nên x2 không thoả mãn điều kiện của ẩn.
Trả lời : Tỉ số tăng dân số trung bình một năm của thành phố này là 0,5%.
64. Giải. Gọi số mà đầu bài đã cho là x, x dương.
Bạn Quân đã chọn số x - 2 để nhân với x.
Vì tích này là 120 nên ta có phương trình : x(x - 2) = 120 hay x2 - 2x - 120 = 0. Giải phương trình ta được số đã cho là 12.
Nhưng đầu bài yêu cầu tìm tích của x với x + 2. Vậy kết quả đúng phải là:
12.14= 168.
Trả lời : Kết quả đúng phải là 168.
65. Giải. Gọi vận tốc của xe lửa thứ nhất là : x (km/h), x > 0.
Khi đó vận tốc của xe lửa thứ hai là : x + 5 (km/h).
Thời gian xe lửa thứ nhất đi từ Hà Nội đến chỗ gặp nhau là : 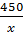 (giờ).
Thời gian xe lửa thứ hai đi từ Bình Sơn đến chỗ gặp nhau là :
(giờ).
Thời gian xe lửa thứ hai đi từ Bình Sơn đến chỗ gặp nhau là : 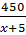 (giờ).
Vì xe lửa thứ hai đi sau 1 giờ ; nghĩa là thời gian đi đến chỗ gặp nhau ít hơn xe lửa thứ nhất 1 giờ. Do đó ta có phương trình :
(giờ).
Vì xe lửa thứ hai đi sau 1 giờ ; nghĩa là thời gian đi đến chỗ gặp nhau ít hơn xe lửa thứ nhất 1 giờ. Do đó ta có phương trình :
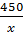 -
- 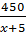 = 1
Giải phương trình : x2 + 5x = 2250 hay x2 + 5x - 2250 = 0.
Ta có :
= 1
Giải phương trình : x2 + 5x = 2250 hay x2 + 5x - 2250 = 0.
Ta có :  = 25 + 9000 = 9025,
= 25 + 9000 = 9025, 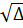 = 95. Vậy x1 = 45, x2 = -50.
Vì x > 0 nên x2 không thoả mãn điều kiện của ẩn.
Trả lời : Vận tốc của xe lửa thứ nhất là 45km/h.
Vận tốc của xe lửa thứ hai là 50km/h.
= 95. Vậy x1 = 45, x2 = -50.
Vì x > 0 nên x2 không thoả mãn điều kiện của ẩn.
Trả lời : Vận tốc của xe lửa thứ nhất là 45km/h.
Vận tốc của xe lửa thứ hai là 50km/h.
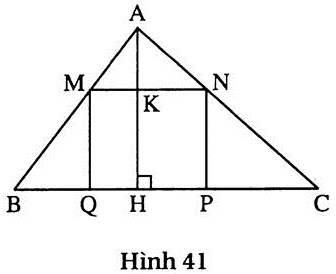
66. Giải. (h.41) Để xác định vị trí của M ta chỉ cần tính độ dài đoạn AK.
Gọi độ dài đoạn AK là x (cm), x > 0.
Vì  ABC đồng dạng với ABC đồng dạng với  AMN nên : AMN nên :
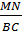 = = 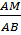 = = 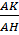 = = 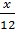
Suy ra : MN = 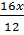 = = 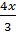
Mặt khác: MQ = KH= 12 - x.
Do đó diện tích của hình chữ nhật MNPQ là : (12 - x). 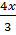
Theo đầu bài ta có phương trình : (12 - x).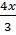 = 36 hay x2 - 12x + 27 = 0. = 36 hay x2 - 12x + 27 = 0.
Giải phương trình ta được : x1 = 3, x2 = 9.
Trả lời : Độ dài của AK bằng 3cm hoặc 9cm. |
 |
D. Bài tập luyện thêm
1. Cho hàm số y - f(x) - (1 - 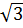 )x2.
a) Hàm số này đồng biến khi nào, nghịch biến khi nào ?
b) Không làm tính, hãy so sánh : f(-5) và f(-1); f(
)x2.
a) Hàm số này đồng biến khi nào, nghịch biến khi nào ?
b) Không làm tính, hãy so sánh : f(-5) và f(-1); f( 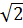 ) và f(
) và f(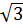 ); f(
); f(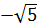 ) và f(1975).
c) Tìm các giá trị của x sao cho 1-
) và f(1975).
c) Tìm các giá trị của x sao cho 1- 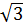
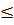 y
y 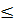 0.
2. Giải phương trình :
a)
0.
2. Giải phương trình :
a) 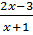 =
= 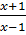 -
- 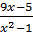 b) 2x3 + x2 + 2(x - 1)2 =14 - 3x2.
3. Một phân xưởng may phải sản xuất 400 sản phẩm trong một thời gian quy định. Làm được 5 ngày theo năng suất dự định thì phân xưởng phải nhận nhiệm vụ sản xuất thêm 70 sản phẩm nữa. Vì thế mỗi ngày phải làm thêm 5 sản phẩm nữa và thời gian phải kéo dài thêm một ngày so với dự định. Hỏi thời gian dự định theo kế hoạch là bao nhiêu ngày ?
Hướng dẫn - Đáp số
1. Giải. a) Vì 1 -
b) 2x3 + x2 + 2(x - 1)2 =14 - 3x2.
3. Một phân xưởng may phải sản xuất 400 sản phẩm trong một thời gian quy định. Làm được 5 ngày theo năng suất dự định thì phân xưởng phải nhận nhiệm vụ sản xuất thêm 70 sản phẩm nữa. Vì thế mỗi ngày phải làm thêm 5 sản phẩm nữa và thời gian phải kéo dài thêm một ngày so với dự định. Hỏi thời gian dự định theo kế hoạch là bao nhiêu ngày ?
Hướng dẫn - Đáp số
1. Giải. a) Vì 1 - 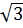 < 0 nên hàm số đống biến khi x < 0 và nghịch biến khi x > 0
b) Vì -5 < -1 < 0 và hàm số đồng biến khi x < 0 nên f(-5) < f(-1).
Vì hàm số nghịch biến khi x > 0 và
< 0 nên hàm số đống biến khi x < 0 và nghịch biến khi x > 0
b) Vì -5 < -1 < 0 và hàm số đồng biến khi x < 0 nên f(-5) < f(-1).
Vì hàm số nghịch biến khi x > 0 và 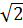 <
< 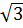 nên f (
nên f (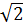 ) > f (
) > f (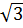 )
Ta có f(
)
Ta có f(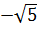 ) = f(
) = f( 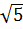 ). Mặt khác,
). Mặt khác, 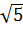 < 1975 và hàm số nghịch biến khi x > 0 nên f(
< 1975 và hàm số nghịch biến khi x > 0 nên f(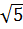 ) > f(1975). Do đó f(
) > f(1975). Do đó f( 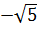 ) > f( 1975).
c) Khi y = 1 -
) > f( 1975).
c) Khi y = 1 - 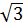 thì (1 -
thì (1 -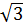 )x2 = 1 -
)x2 = 1 -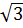 . Suy ra x = -1 hoặc x = 1.
Như vậy 1 -
. Suy ra x = -1 hoặc x = 1.
Như vậy 1 - 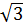 = f(-1) = f(1). Hơn nữa f(0) = 0.
Xét trường hợp x
= f(-1) = f(1). Hơn nữa f(0) = 0.
Xét trường hợp x 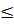 0. Vì hàm số đồng biến khi x < 0 nên khi 1 -
0. Vì hàm số đồng biến khi x < 0 nên khi 1 -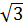
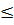 y
y 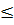 0, tức là khi f(-1)
0, tức là khi f(-1) 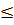 y
y 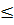 f(0) thì -1
f(0) thì -1 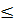 x
x 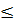 0.
Xét trường hợp x
0.
Xét trường hợp x 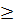 0. Vì hàm số nghịch biến khi x > 0 nên khi 1 -
0. Vì hàm số nghịch biến khi x > 0 nên khi 1 -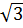
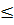 y
y 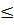 0.
tức là khi f(1)
0.
tức là khi f(1) 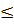 y
y 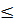 f(0) thì 1
f(0) thì 1 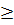 x
x 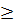 0.
Vậy khi 1 -
0.
Vậy khi 1 - 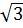
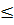 y
y 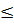 0 thì -1
0 thì -1 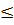 x
x 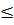 1.
2. a) Đáp số: x = -3.
b) Giải. 2x3 + x2 + 2(x - 1)2 = 14 - 3x2
⇔ 2x3 + x2 + 2(x2 - 2x + 1) - 14 + 3x2 = 0
⇔ 2x3 + 6x2 - 4x - 12 = 0 ⇔ 2x2(x + 3) - 4(x + 3) = 0
⇔ (x + 3)(2x2 - 4) = 0
⇔
1.
2. a) Đáp số: x = -3.
b) Giải. 2x3 + x2 + 2(x - 1)2 = 14 - 3x2
⇔ 2x3 + x2 + 2(x2 - 2x + 1) - 14 + 3x2 = 0
⇔ 2x3 + 6x2 - 4x - 12 = 0 ⇔ 2x2(x + 3) - 4(x + 3) = 0
⇔ (x + 3)(2x2 - 4) = 0
⇔ 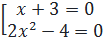 ⇔
⇔ 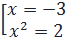 ⇔
⇔ 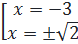 3. Giải. Gọi thời gian dự định là x (ngày), x > 0.
Thế thì năng suất dự định mỗi ngày là
3. Giải. Gọi thời gian dự định là x (ngày), x > 0.
Thế thì năng suất dự định mỗi ngày là 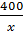 sản phẩm.
Số sản phẩm làm được trong 5 ngày là 5.
sản phẩm.
Số sản phẩm làm được trong 5 ngày là 5.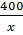 hay
hay 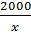 Số sản phẩm còn phải sản xuất tiếp là 470 -
Số sản phẩm còn phải sản xuất tiếp là 470 - 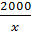 hay
hay 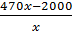 Vì thời gian kéo dài thêm 1 ngày nên thời gian thực làm là x + 1 ngày.
Do đó số thời gian phải làm tiếp sau 5 ngày là x + 1 - 5 hay x - 4 ngày.
Năng suất mỗi ngày sau là :
Vì thời gian kéo dài thêm 1 ngày nên thời gian thực làm là x + 1 ngày.
Do đó số thời gian phải làm tiếp sau 5 ngày là x + 1 - 5 hay x - 4 ngày.
Năng suất mỗi ngày sau là : 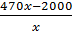 : (x - 4) hay
: (x - 4) hay  sản phẩm.
Theo đầu bài, mỗi ngày sau làm hơn mỗi ngày trong 5 ngày đầu là 5 sản phẩm nên ta có phương trình:
sản phẩm.
Theo đầu bài, mỗi ngày sau làm hơn mỗi ngày trong 5 ngày đầu là 5 sản phẩm nên ta có phương trình:
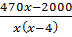 -
- 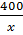 = 5 hay 470x - 2000 - 400(x - 4) = 5x(x - 4)
hay x2 – 18x + 80 = 0
Ta có: '
= 5 hay 470x - 2000 - 400(x - 4) = 5x(x - 4)
hay x2 – 18x + 80 = 0
Ta có: '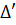 = 92 – 80 = l.
Vậy x1 = 9 + 1 = 10, x2 = 9 - 1 = 8.
Hai giá trị tìm được đều thoả mãn điều kiện của ẩn.
Trả lời : Thời gian dự định là 10 ngày hoặc 8 ngày.
Lưu ý. Trên đây ta đã dùng mối liên quan giữa năng suất dự định và năng suất làm việc trong những ngày sau để lập phương trình. Tuy nhiên trong đầu bài còn có mối liên quan giữa thời gian dự định và thời gian thực làm. Do đó ta cũng có thể dùng mối liên quan này để lập phương trình.
Ta biết thời gian dự định là x ngày và thời gian thực làm là x + 1 ngày. Thời gian thực làm này gồm 5 ngày đầu và thời gian hoàn thành nốt công việc. Vậy ta cần biểu diễn thời gian hoàn thành nốt công việc. Có thể lập luận như sau :
Trong 5 ngày đầu mỗi ngày sản xuất được
= 92 – 80 = l.
Vậy x1 = 9 + 1 = 10, x2 = 9 - 1 = 8.
Hai giá trị tìm được đều thoả mãn điều kiện của ẩn.
Trả lời : Thời gian dự định là 10 ngày hoặc 8 ngày.
Lưu ý. Trên đây ta đã dùng mối liên quan giữa năng suất dự định và năng suất làm việc trong những ngày sau để lập phương trình. Tuy nhiên trong đầu bài còn có mối liên quan giữa thời gian dự định và thời gian thực làm. Do đó ta cũng có thể dùng mối liên quan này để lập phương trình.
Ta biết thời gian dự định là x ngày và thời gian thực làm là x + 1 ngày. Thời gian thực làm này gồm 5 ngày đầu và thời gian hoàn thành nốt công việc. Vậy ta cần biểu diễn thời gian hoàn thành nốt công việc. Có thể lập luận như sau :
Trong 5 ngày đầu mỗi ngày sản xuất được 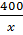 sản phẩm.
Như vậy trong 5 ngày sản xuất được
sản phẩm.
Như vậy trong 5 ngày sản xuất được 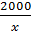 sản phẩm.
Số sản phẩm còn phải sản xuất tiếp là
sản phẩm.
Số sản phẩm còn phải sản xuất tiếp là 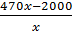 sản phẩm.
Vì năng suất ở thời gian sau tăng thêm 5 sản phẩn nên mỗi ngày sau sản xuất được:
sản phẩm.
Vì năng suất ở thời gian sau tăng thêm 5 sản phẩn nên mỗi ngày sau sản xuất được:
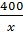 + 5 hay
+ 5 hay 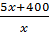 sản phẩm
Do đó thời gian cần làm nốt công việc là:
sản phẩm
Do đó thời gian cần làm nốt công việc là:
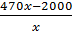 :
: 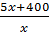 hay
hay 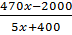 ngày.
Vì tổng thời gian làm việc là x + 1 nên ta có phương trình :
ngày.
Vì tổng thời gian làm việc là x + 1 nên ta có phương trình :
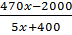 + 5 = x + 1 hay
+ 5 = x + 1 hay 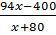 – x + 4 = 0 hay x2 – 18x + 80 = 0
– x + 4 = 0 hay x2 – 18x + 80 = 0
© Bản quyền thuộc về
Bài kiểm tra. Ghi rõ nguồn Bài kiểm tra.com khi sao chép nội dung này.



