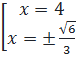Giải bài tập Toán 9, chương IV, bài 7: Phương trình quy về phương trình bậc hai
2019-08-26T06:03:16-04:00
2019-08-26T06:03:16-04:00
Giải bài tập Toán 9, chương IV, bài 7: Phương trình quy về phương trình bậc hai : Tóm tắt kiến thức, ví dụ, hướng dẫn giải bài tập trong sách giáo khoa và bài tập luyện thêm.
/themes/cafe/images/no_image.gif
Bài Kiểm Tra
https://baikiemtra.com/uploads/bai-kiem-tra-logo.png
Thứ hai - 26/08/2019 05:56
Giải bài tập Toán 9, chương IV, bài 7: Phương trình quy về phương trình bậc hai : Tóm tắt kiến thức, ví dụ, hướng dẫn giải bài tập trong sách giáo khoa và bài tập luyện thêm.
A. Tóm tắt kiến thức
1. Phương trình trùng phương
Phương trình trùng phương là phương trình có dạng
ax4 + bx2 + c = 0 (a 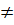 0). (1)
Cách giải. Đặt t = x2, t
0). (1)
Cách giải. Đặt t = x2, t 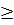 0, ta được phương trình bậc hai đối với ẩn t : at2 + bt + c = 0. (2)
Giải phương trình (2).
Thay mỗi giá trị không âm tìm được của t vào đẳng thức x2 = t, ta tìm được x =
0, ta được phương trình bậc hai đối với ẩn t : at2 + bt + c = 0. (2)
Giải phương trình (2).
Thay mỗi giá trị không âm tìm được của t vào đẳng thức x2 = t, ta tìm được x = 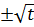 .
2. Phương trình chứa ẩn ở mẫu thức
Khi giải phương trình chứa ẩn ở mẫu thức ta làm như sau :
Bước 1. Tìm điều kiện xác định của phương trình ;
Bước 2. Quy đồng mẫu thức hai vế rồi khử mẫu ;
Bước 3. Giải phương trình vừa nhận được ;
Bước 4. Trong các giá trị tìm được của ẩn, loại các giá trị không thoả mãn điều kiện xác định, các giá trị thoả mãn điều kiện xác định là nghiệm của phương trình đã cho.
3. Phương trình tích
A(x).B(x) = 0 ⇔A(x) = 0 hoặc B(x) = 0.
4. Đặt ẩn phụ
Ta có thể giải phương trình A[f(x)]2 + Bf(x) + c = 0 bằng cách đặt ẩn phụ t =f(x).
B. Ví dụ
Ví dụ 1. Giải phương trình trùng phương :
.
2. Phương trình chứa ẩn ở mẫu thức
Khi giải phương trình chứa ẩn ở mẫu thức ta làm như sau :
Bước 1. Tìm điều kiện xác định của phương trình ;
Bước 2. Quy đồng mẫu thức hai vế rồi khử mẫu ;
Bước 3. Giải phương trình vừa nhận được ;
Bước 4. Trong các giá trị tìm được của ẩn, loại các giá trị không thoả mãn điều kiện xác định, các giá trị thoả mãn điều kiện xác định là nghiệm của phương trình đã cho.
3. Phương trình tích
A(x).B(x) = 0 ⇔A(x) = 0 hoặc B(x) = 0.
4. Đặt ẩn phụ
Ta có thể giải phương trình A[f(x)]2 + Bf(x) + c = 0 bằng cách đặt ẩn phụ t =f(x).
B. Ví dụ
Ví dụ 1. Giải phương trình trùng phương :
a) x4 - 8x2 + 7 = 0
c) 2x4 + 7x2 + 5 = 0;
e) 5x4 - 14x2 + 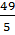 = 0. = 0. |
b) 3x4 + 10x2 - 8 = 0;
d)7x4 - 28x2 = 0;
|
Giải: a) Đặt t = x2, t 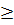 0, ta được : t2 - 8t + 7 = 0.
Vì 1 - 8 + 7 = 0 nên phương trình này có hai nghiệm : t1 = 1, t2 = 7.
Với t = 1, ta có x2 = 1. Do đó x1 = 1 ; x2 = -1.
Với t = 7, ta có x2 = 7. Do đó x3 =
0, ta được : t2 - 8t + 7 = 0.
Vì 1 - 8 + 7 = 0 nên phương trình này có hai nghiệm : t1 = 1, t2 = 7.
Với t = 1, ta có x2 = 1. Do đó x1 = 1 ; x2 = -1.
Với t = 7, ta có x2 = 7. Do đó x3 = 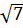 , x4 =
, x4 = 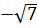 .
Vậy phương trình đã cho có bốn nghiệm : x1 = 1 ; x2 = -1, x3 =
.
Vậy phương trình đã cho có bốn nghiệm : x1 = 1 ; x2 = -1, x3 = 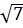 , x4 =
, x4 = 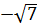 .
b) Đặt t = x2, t
.
b) Đặt t = x2, t 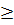 0, ta được : 3t2 + 10t - 8 = 0.
'
0, ta được : 3t2 + 10t - 8 = 0.
'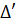 = 25 - 3.(-8) = 49.
t1 =
= 25 - 3.(-8) = 49.
t1 = 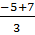 =
=  ; t2 =
; t2 = 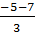 = - 4
Vì t
= - 4
Vì t 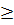 0 nên t2 = - 4 bị loại.
Với t =
0 nên t2 = - 4 bị loại.
Với t =  , ta có x2 =
, ta có x2 =  .
Vậy phương trình đã cho có hai nghiệm là :
x1 =
.
Vậy phương trình đã cho có hai nghiệm là :
x1 = 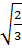 , x2 =
, x2 = 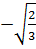 hay x1 =
hay x1 = 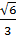 , x2 =
, x2 = 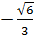 c) Đặt t = x2, t
c) Đặt t = x2, t 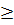 0, ta được : 2t2 + 7t + 5 = 0.
Vì 2 -7 + 5= 0 nên phương trình này có hai nghiệm là :
t1 = - 1 (loại), t2 = -1 (loại).
Vậy phương trình đã cho vô nghiệm.
d) Đặt t = x2, t
0, ta được : 2t2 + 7t + 5 = 0.
Vì 2 -7 + 5= 0 nên phương trình này có hai nghiệm là :
t1 = - 1 (loại), t2 = -1 (loại).
Vậy phương trình đã cho vô nghiệm.
d) Đặt t = x2, t 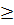 0, ta được : 7t2 - 28t = 0.
Phương trình này có hai nghiệm là t1 = 0, t2 = 4.
Với t = 0, ta có x2 = 0. Do đó x = 0.
Với t = 4, ta có x2 = 4. Do đó x = 2 hoặc x = -2.
Vậy phương trình đã cho có ba nghiệm là :
x1 = 0, x2 = 2, x3 = -2.
e) Đặt t = x2 , t ≥
0, ta được : 7t2 - 28t = 0.
Phương trình này có hai nghiệm là t1 = 0, t2 = 4.
Với t = 0, ta có x2 = 0. Do đó x = 0.
Với t = 4, ta có x2 = 4. Do đó x = 2 hoặc x = -2.
Vậy phương trình đã cho có ba nghiệm là :
x1 = 0, x2 = 2, x3 = -2.
e) Đặt t = x2 , t ≥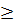 0, ta được : 5t2 - 14t +
0, ta được : 5t2 - 14t + 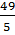 = 0 hay 25t - 70t + 49 = 0.
'
= 0 hay 25t - 70t + 49 = 0.
'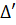 = 1225 - 1225 = 0.
Phương trình này có nghiệm kép: t1 = t2 =
= 1225 - 1225 = 0.
Phương trình này có nghiệm kép: t1 = t2 = 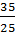 =
=  Với t =
Với t =  ; ta có x2 =
; ta có x2 =  Vậy phương trình đã cho có hai nghiệm là:
x1 =
Vậy phương trình đã cho có hai nghiệm là:
x1 = 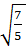 , x2 =
, x2 = 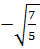 hay x1 =
hay x1 = 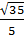 , x2 =
, x2 = 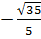 Ví dụ 2: Giải phương trình:
a)
Ví dụ 2: Giải phương trình:
a) 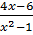 =
= 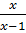 -
- 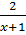 ; b)
; b) 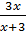 +
+ 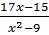 =
= 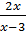 c)
c) 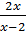 -
- 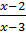 =
= 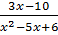 Giải: a) Điều kiện: x
Giải: a) Điều kiện: x 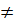
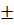 1
1
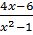 =
= 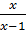 -
- 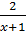 ⇒ 4x – 6 = x(x+1) – 2x(x -1)
⇔ 4x – 6 = x2 + x – 2x2 + 2x ⇔ x2 + x - 6 = 0
⇒ 4x – 6 = x(x+1) – 2x(x -1)
⇔ 4x – 6 = x2 + x – 2x2 + 2x ⇔ x2 + x - 6 = 0
 = 1 + 4.6 = 25
x1 =
= 1 + 4.6 = 25
x1 = 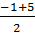 = 2 ; x2 =
= 2 ; x2 = 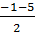 = -3
Vì x1 = 2, x2 = -3 đều thoả mãn điểu kiện của ẩn nên chúng là hai nghiệm của phương trình.
b) Điều kiện : x
= -3
Vì x1 = 2, x2 = -3 đều thoả mãn điểu kiện của ẩn nên chúng là hai nghiệm của phương trình.
b) Điều kiện : x 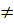
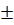 3.
3.
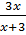 +
+ 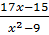 =
= 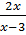 ⇒ 3x(x -3) + 17x – 15 = 2x(x+3)
⇔ 3x2 – 9x + 17x – 15 = 2x2 + 6x ⇔ x2 + 2x – 15 = 0
'
⇒ 3x(x -3) + 17x – 15 = 2x(x+3)
⇔ 3x2 – 9x + 17x – 15 = 2x2 + 6x ⇔ x2 + 2x – 15 = 0
'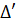 = 1 + 15 = 16
'
= 1 + 15 = 16
'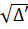 = 4
x1 = -1 + 4 = 3, x2 = - 1 – 4 = - 5
Vì x1 = 3 không thoả mãn điều kiện của ẩn nên phương trình chỉ có một nghiệm là x2 = -5.
c) Điều kiện : x
= 4
x1 = -1 + 4 = 3, x2 = - 1 – 4 = - 5
Vì x1 = 3 không thoả mãn điều kiện của ẩn nên phương trình chỉ có một nghiệm là x2 = -5.
c) Điều kiện : x 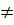 2, x
2, x 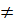 3.
3.
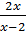 -
- 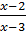 =
= 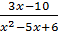 ⇒ 2x(x – 3) – (x – 2)(x - 2) = 3x – 10
⇔ 2x2 – 6x – x2 + 4x – 4 = 3x – 10 ⇔ x2 - 5x + 6 = 0.
⇒ 2x(x – 3) – (x – 2)(x - 2) = 3x – 10
⇔ 2x2 – 6x – x2 + 4x – 4 = 3x – 10 ⇔ x2 - 5x + 6 = 0.
 = 25 - 4.6 = 1
Cả hai giá trị tìm được của x đều không thoả mãn điều kiện của ẩn.
Vậy phương trình vô nghiệm.
Ví dụ 3. Giải phương trình :
a) (2x2 + 3x + 1)2 = (x2 + 2x + 1)2 ;
b) x4 - 5x3 + 20x - 16 = 0;
c) (2x2 - x + 1)2 - 4x2 + 2x- 1 = 0;
d) x4 + 2x3 + 5x2 + 4x - 5 = 0.
❖ Phân tích: a) Nếu chuyển vế ta được hiệu của hai bình phương. Do đó có thể đưa phương trình đã cho về phương trình tích.
b) Nhận thấy có thể phân tích vế trái thành nhân tử bằng cách nhóm nhiều hạng tử.
c) Nhận thấy - 4x2 + 2x = -2(2x2 - x). Do đó có thể viết:
-4x2 + 2x = -2(2x2 - x + 1) + 2 và có thể đặt ẩn phụ t = 2x2 - x + 1.
d) Nhận thấy x4 + 2x3 + x2 = (x2 + x)2. Cần xét xem có thể đặt ẩn phụ t = x2 + x hay không.
Giải: a) (2x2 + 3x + 1)2 = (x2 + 2x + 1)2 ⇔ (2x2 + 3x + 1)2 - (x2 + 2x + 1)2 = 0
⇔ (2x2 + 3x + 1 + x2 + 2x + 1)(2x2 + 3x + 1 – x2 - 2x - 1) = 0
⇔ (3x2 + 5x + 2)(x2 + x) = 0 ⇔ 3x2 + 5x + 2 = 0 hoặc x2 + x = 0.
Giải phương trình 3x2 + 5x + 2 = 0.
Vì 3 - 5 + 2 = 0 nên phương trình có hai nghiệm là x = -1, x =
= 25 - 4.6 = 1
Cả hai giá trị tìm được của x đều không thoả mãn điều kiện của ẩn.
Vậy phương trình vô nghiệm.
Ví dụ 3. Giải phương trình :
a) (2x2 + 3x + 1)2 = (x2 + 2x + 1)2 ;
b) x4 - 5x3 + 20x - 16 = 0;
c) (2x2 - x + 1)2 - 4x2 + 2x- 1 = 0;
d) x4 + 2x3 + 5x2 + 4x - 5 = 0.
❖ Phân tích: a) Nếu chuyển vế ta được hiệu của hai bình phương. Do đó có thể đưa phương trình đã cho về phương trình tích.
b) Nhận thấy có thể phân tích vế trái thành nhân tử bằng cách nhóm nhiều hạng tử.
c) Nhận thấy - 4x2 + 2x = -2(2x2 - x). Do đó có thể viết:
-4x2 + 2x = -2(2x2 - x + 1) + 2 và có thể đặt ẩn phụ t = 2x2 - x + 1.
d) Nhận thấy x4 + 2x3 + x2 = (x2 + x)2. Cần xét xem có thể đặt ẩn phụ t = x2 + x hay không.
Giải: a) (2x2 + 3x + 1)2 = (x2 + 2x + 1)2 ⇔ (2x2 + 3x + 1)2 - (x2 + 2x + 1)2 = 0
⇔ (2x2 + 3x + 1 + x2 + 2x + 1)(2x2 + 3x + 1 – x2 - 2x - 1) = 0
⇔ (3x2 + 5x + 2)(x2 + x) = 0 ⇔ 3x2 + 5x + 2 = 0 hoặc x2 + x = 0.
Giải phương trình 3x2 + 5x + 2 = 0.
Vì 3 - 5 + 2 = 0 nên phương trình có hai nghiệm là x = -1, x = 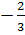 Giải phương trình x2 + x = 0.
Đưa về phương trình tích x(x + 1) = 0.
Phương trình có hai nghiệm : x = 0, x = -1.
Vậy phương trình có ba nghiệm : x1= -1, x2 = 0, x3 =
Giải phương trình x2 + x = 0.
Đưa về phương trình tích x(x + 1) = 0.
Phương trình có hai nghiệm : x = 0, x = -1.
Vậy phương trình có ba nghiệm : x1= -1, x2 = 0, x3 = 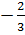 .
b) x4 - 5x3 + 20x - 16 = 0 ⇔ x4 - 16 - (5x3 - 20x) = 0
⇔ (x2 - 4)(x2 + 4) - 5x(x2 - 4) = 0 (x2 - 4)(x2 + 4 - 5x) = 0
⇔ (x - 2)(x + 2)(x2 -5x + 4) = 0 ⇔ x = 2 hoặc x = -2 hoặc x2 - 5x + 4 = 0.
Phương trình x2 - 5x + 4 = 0 có hai nghiệm là x = 1 và x = 4 vì 1 -5 + 4 = 0.
Vậy phương trình đã cho có bốn nghiệm : x = 2, x = -2, x = 1, x = 4.
c) Phương trình (2x2 - x + 1)2 - 4x2 + 2x- 1 = 0 có thể viết thành:
(2x2 - x + 1)2 - (4x2 - 2x + 2) + 1 =0 hay (2x2 – x + 1)2 - 2(2x2 - x+ 1)+ 1 = 0.
Đặt ẩn phụ t = 2x2 - x + 1, ta được :
t2 - 2t + 1 = 0 ⇔ (t - 1)2 = 0 ⇔ t = 1.
Do đó ta có phương trình : 2x2 - x + 1 = 1 hay 2x2 - x = 0 hay x(2x - 1) = 0.
Vậy phương trình có hai nghiệm là x = 0, x =
.
b) x4 - 5x3 + 20x - 16 = 0 ⇔ x4 - 16 - (5x3 - 20x) = 0
⇔ (x2 - 4)(x2 + 4) - 5x(x2 - 4) = 0 (x2 - 4)(x2 + 4 - 5x) = 0
⇔ (x - 2)(x + 2)(x2 -5x + 4) = 0 ⇔ x = 2 hoặc x = -2 hoặc x2 - 5x + 4 = 0.
Phương trình x2 - 5x + 4 = 0 có hai nghiệm là x = 1 và x = 4 vì 1 -5 + 4 = 0.
Vậy phương trình đã cho có bốn nghiệm : x = 2, x = -2, x = 1, x = 4.
c) Phương trình (2x2 - x + 1)2 - 4x2 + 2x- 1 = 0 có thể viết thành:
(2x2 - x + 1)2 - (4x2 - 2x + 2) + 1 =0 hay (2x2 – x + 1)2 - 2(2x2 - x+ 1)+ 1 = 0.
Đặt ẩn phụ t = 2x2 - x + 1, ta được :
t2 - 2t + 1 = 0 ⇔ (t - 1)2 = 0 ⇔ t = 1.
Do đó ta có phương trình : 2x2 - x + 1 = 1 hay 2x2 - x = 0 hay x(2x - 1) = 0.
Vậy phương trình có hai nghiệm là x = 0, x =  d) Phương trình x4 + 2x3 + 5x2 + 4x - 5 = 0 có thể viết thành:
x4 + 2x3 + x2 + 4x2 + 4x - 5 = 0 hay (x2 + x)2 + 4(x2 + x) - 5 = 0.
Đặt t = x2 + x, ta được : t2 + 4t - 5 = 0. (*)
Vì 1 + 4 - 5 = 0 nên phương trình (*) có hai nghiệm là : t = 1, t = -5.
+ Với t = l ta có x2 + x = 1 hay x2 + x - l = 0.
d) Phương trình x4 + 2x3 + 5x2 + 4x - 5 = 0 có thể viết thành:
x4 + 2x3 + x2 + 4x2 + 4x - 5 = 0 hay (x2 + x)2 + 4(x2 + x) - 5 = 0.
Đặt t = x2 + x, ta được : t2 + 4t - 5 = 0. (*)
Vì 1 + 4 - 5 = 0 nên phương trình (*) có hai nghiệm là : t = 1, t = -5.
+ Với t = l ta có x2 + x = 1 hay x2 + x - l = 0.
 = 12 - 4.1.(-1) = 5.
Phương trình có hai nghiệm là : x =
= 12 - 4.1.(-1) = 5.
Phương trình có hai nghiệm là : x = 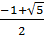 , x2 =
, x2 = 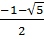 .
+ Với t = -5, ta có x2 + x = -5 hay x2 + x + 5 = 0.
.
+ Với t = -5, ta có x2 + x = -5 hay x2 + x + 5 = 0.
 = 12 - 4.1.5 = -19 < 0.
Phương trình này vô nghiệm.
Vậy phương trình đã cho có hai nghiệm là : x =
= 12 - 4.1.5 = -19 < 0.
Phương trình này vô nghiệm.
Vậy phương trình đã cho có hai nghiệm là : x = 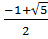 , x =
, x = 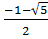 C. Hướng dẫn giải bài tập trong sách giáo khoa
34. Giải: a) Đặt t = x2, t
C. Hướng dẫn giải bài tập trong sách giáo khoa
34. Giải: a) Đặt t = x2, t 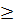 0, ta được : t2 - 5t + 4 = 0. (*)
Vì 1 - 5 + 4 = 0 nên phương trình (*) có hai nghiệm là t = 1, t = 4.
Với t = 1, ta có : x2 = 1 ⇔ x = 1 hoặc x =- l.
Với t = 4, ta có : x2 = 4 ⇔ x = 2, x = -2.
Vậy phương trình đã cho có bốn nghiệm : x = 1, x = - 1, x = 2, x = -2.
b) Đặt t = x2, t
0, ta được : t2 - 5t + 4 = 0. (*)
Vì 1 - 5 + 4 = 0 nên phương trình (*) có hai nghiệm là t = 1, t = 4.
Với t = 1, ta có : x2 = 1 ⇔ x = 1 hoặc x =- l.
Với t = 4, ta có : x2 = 4 ⇔ x = 2, x = -2.
Vậy phương trình đã cho có bốn nghiệm : x = 1, x = - 1, x = 2, x = -2.
b) Đặt t = x2, t 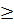 0, ta được : 2t2 - 3t - 2 = 0.
0, ta được : 2t2 - 3t - 2 = 0.
 = 9 - 4.2.(-2) = 25. Vậy
= 9 - 4.2.(-2) = 25. Vậy 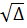 = 5.
Ta có : t1 =
= 5.
Ta có : t1 = 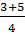 = 2, t2 =
= 2, t2 = 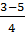 =
= 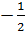 (loại).
Với t = 2, ta có x2 = 2 ⇔ x =
(loại).
Với t = 2, ta có x2 = 2 ⇔ x = 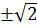 .
Vậy phương trình đã cho có hai nghiệm là x =
.
Vậy phương trình đã cho có hai nghiệm là x = 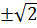 .
c) Đặt t = x2, t
.
c) Đặt t = x2, t 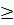 0, ta được : 3t2 + 10t + 3 = 0.
'
0, ta được : 3t2 + 10t + 3 = 0.
'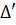 = 25 - 9 = 16. Vậy '
= 25 - 9 = 16. Vậy '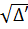 =4.
Ta có : t1 =
=4.
Ta có : t1 = 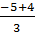 =
= 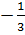 (loại), t2 =
(loại), t2 = 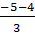 =
= 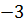 (loại).
Phương trình đã cho vô nghiệm.
35. Giải: a)
(loại).
Phương trình đã cho vô nghiệm.
35. Giải: a) 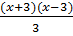 + 2 = x(1 - x) ⇔ x2 - 9 + 6 = 3x - 3x2
⇔ 4x2 - 3x - 3 = 0.
+ 2 = x(1 - x) ⇔ x2 - 9 + 6 = 3x - 3x2
⇔ 4x2 - 3x - 3 = 0.
 = 9 - 4.4.(-3) = 57,
= 9 - 4.4.(-3) = 57, 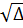 =
= 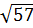 .
x1 =
.
x1 = 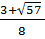 ; x2 =
; x2 = 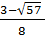 b) Điều kiện : x
b) Điều kiện : x 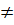 5, x
5, x 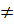 2.
2.
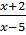 + 3 =
+ 3 = 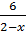 ⇒ (x + 2)(2 - x) + 3(x - 5)(2 - x) = 6(x - 5)
⇔ - x2 + 4 + 3(-x2 + 7x - 10) = 6x - 30 ⇔ 4x2 - 15x - 4 = 0.
⇒ (x + 2)(2 - x) + 3(x - 5)(2 - x) = 6(x - 5)
⇔ - x2 + 4 + 3(-x2 + 7x - 10) = 6x - 30 ⇔ 4x2 - 15x - 4 = 0.
 = 225 - 4.4.(-4) = 289. Vậy
= 225 - 4.4.(-4) = 289. Vậy 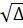 = 17.
x1 =
= 17.
x1 = 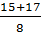 = 4 ; x2 =
= 4 ; x2 = 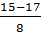 =
= 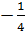 c) Điều kiện : x
c) Điều kiện : x 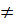 -1, x
-1, x 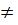 -2.
-2.
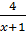 =
= 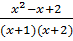 ⇒ 4(x+2) = -x2 - x + 2x2 + 5x + 6 = 0.
⇒ 4(x+2) = -x2 - x + 2x2 + 5x + 6 = 0.
 = 25 - 4.1.6 = 1.
x1 =
= 25 - 4.1.6 = 1.
x1 = 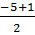 = -2 (loại), x2 =
= -2 (loại), x2 = 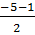 = -3 .
36. Giải. Lưu ý. Để trình bày lời giải gọn hơn, ta có thể dùng kí hiệu “[” thay cho từ hoặc.
a) (3x2 - 5x + 1)(x2 - 4) = 0 ⇔
= -3 .
36. Giải. Lưu ý. Để trình bày lời giải gọn hơn, ta có thể dùng kí hiệu “[” thay cho từ hoặc.
a) (3x2 - 5x + 1)(x2 - 4) = 0 ⇔ 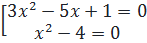 ⇔
⇔ 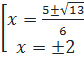 b) (2x2 + x - 4)2 - (2x - 1)2 = 0
⇔ (2x2 + x - 4 + 2x - 1)(2x2 + x – 4 - 2x + 1) = 0
⇔ (2x2+ 3x - 5)(2x2 - x - 3) = 0 ⇔
b) (2x2 + x - 4)2 - (2x - 1)2 = 0
⇔ (2x2 + x - 4 + 2x - 1)(2x2 + x – 4 - 2x + 1) = 0
⇔ (2x2+ 3x - 5)(2x2 - x - 3) = 0 ⇔ 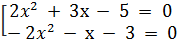 x1 = 1, x2 = -2,5, x3 = -1, x4 = 1,5.
37. Giải: a) 9x4 -10x2 +1= 0. Đặt t = x2
x1 = 1, x2 = -2,5, x3 = -1, x4 = 1,5.
37. Giải: a) 9x4 -10x2 +1= 0. Đặt t = x2 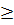 0, ta có : 9t2 - 10t + 1 = 0.
Vì a + b + c = 9 -10 +1= 0 nên t1 = 1, t2 =
0, ta có : 9t2 - 10t + 1 = 0.
Vì a + b + c = 9 -10 +1= 0 nên t1 = 1, t2 =  .
x1 = -1, x2= 1, x3 =
.
x1 = -1, x2= 1, x3 = 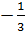 , x4 =
, x4 =  b) 5x4 + 2x2 - 16 = 10 – x2 ⇔ 5x4 + 3x2 - 26 = 0.
Đặt t = x2
b) 5x4 + 2x2 - 16 = 10 – x2 ⇔ 5x4 + 3x2 - 26 = 0.
Đặt t = x2 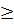 0, ta có : 5t2 + 3t - 26 = 0.
0, ta có : 5t2 + 3t - 26 = 0.
 = 9 + 4.5.26 = 529 = 232. Ta có : t1 = 2, t2 = -2,6 (loại).
x1 =
= 9 + 4.5.26 = 529 = 232. Ta có : t1 = 2, t2 = -2,6 (loại).
x1 = 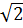 , x2 =
, x2 = 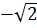 c) 0,3x4 + 1,8x2 + 1,5 = 0 ⇔ x4 + 6x2 + 5 = 0.
Đặt t = x2
c) 0,3x4 + 1,8x2 + 1,5 = 0 ⇔ x4 + 6x2 + 5 = 0.
Đặt t = x2 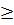 0, ta có : t2 + 6t + 5 = 0. Ta có : t1 = -1 (loại), t2 = -5 (loại).
Phương trình vô nghiệm.
Lưu ý. Cũng có thể nhận xét rằng vế trái x4 + 6x2 + 5
0, ta có : t2 + 6t + 5 = 0. Ta có : t1 = -1 (loại), t2 = -5 (loại).
Phương trình vô nghiệm.
Lưu ý. Cũng có thể nhận xét rằng vế trái x4 + 6x2 + 5 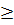 5, còn vế phải bằng 0. Vậy phương trình vô nghiệm.
d) Điều kiện : x
5, còn vế phải bằng 0. Vậy phương trình vô nghiệm.
d) Điều kiện : x 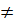 0.
2x2+1 =
0.
2x2+1 = 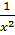 - 4 ⇔ 2x2 + 5 -
- 4 ⇔ 2x2 + 5 - 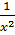 = 0 ⇒ 2x4+ 5x2 - 1 = 0.
Đặt t = x2
= 0 ⇒ 2x4+ 5x2 - 1 = 0.
Đặt t = x2 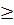 0, ta có : 2t2 + 5t - 1 = 0.
0, ta có : 2t2 + 5t - 1 = 0.
 = 25 + 8 = 33. Ta có : t1 =
= 25 + 8 = 33. Ta có : t1 = 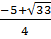 ; t2 =
; t2 = 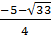 (loại).
x1 =
(loại).
x1 = 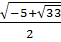 ; x2 =
; x2 = 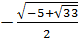 38. Giải: a) (x - 3)2 + (x + 4)2 = 23 - 3x ⇔ x2 - 6x + 9 + x2 + 8x + 16 = 23 - 3x
⇔ 2x2 + 5x + 2 = 0.
38. Giải: a) (x - 3)2 + (x + 4)2 = 23 - 3x ⇔ x2 - 6x + 9 + x2 + 8x + 16 = 23 - 3x
⇔ 2x2 + 5x + 2 = 0.
 = 25 - 16 = 9.
x1= - 2, x2 =
= 25 - 16 = 9.
x1= - 2, x2 = 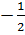 .
b) x3 + 2x2 - (x - 3)2 = (x - 1)(x2 - 2)
⇔ x3 + 2x2 – x2 + 6x - 9 = x3 – x2 - 2x + 2 ⇔ 2x2 + 8x - 11 = 0.
'
.
b) x3 + 2x2 - (x - 3)2 = (x - 1)(x2 - 2)
⇔ x3 + 2x2 – x2 + 6x - 9 = x3 – x2 - 2x + 2 ⇔ 2x2 + 8x - 11 = 0.
'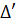 = 16 + 22 = 38.
x1 =
= 16 + 22 = 38.
x1 = 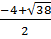 ; x2 =
; x2 = 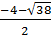 c) (x - 1)3 + 0,5x2 = x(x2 + 1,5) ⇔ x3 - 3x2 + 3x - 1 + 0,5x2 = x3 + 1,5x
⇔ 2,5x2 - 1,5x + 1 = 0 ⇔ 5x2 - 3x + 2 = 0. Ta có :
c) (x - 1)3 + 0,5x2 = x(x2 + 1,5) ⇔ x3 - 3x2 + 3x - 1 + 0,5x2 = x3 + 1,5x
⇔ 2,5x2 - 1,5x + 1 = 0 ⇔ 5x2 - 3x + 2 = 0. Ta có :  = 9 - 40 < 0.
Phương trình vô nghiệm.
d)
= 9 - 40 < 0.
Phương trình vô nghiệm.
d) 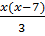 – 1 =
– 1 =  -
- 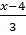 ⇔ 2x(x -7) - 6 = 3x - 2(x - 4)
⇔ 2x2 - 4x - 6 = 3x - 2x + 8 ⇔ 2x2 -15x -14 = 0.
⇔ 2x(x -7) - 6 = 3x - 2(x - 4)
⇔ 2x2 - 4x - 6 = 3x - 2x + 8 ⇔ 2x2 -15x -14 = 0.
 = 225 + 112 = 337.
x1 =
= 225 + 112 = 337.
x1 = 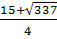 , x2 =
, x2 = 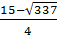 e) Điều kiện : x
e) Điều kiện : x 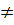
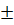 3. Ta có :
3. Ta có : 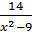 = 1 -
= 1 - 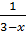 ⇒ 14 = x2 - 9 + x + 3
⇔ x2 + x - 20 = 0.
x1 = 4, x2 = -5.
f) Điều kiện : x
⇒ 14 = x2 - 9 + x + 3
⇔ x2 + x - 20 = 0.
x1 = 4, x2 = -5.
f) Điều kiện : x 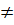 -1, x
-1, x 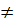 4. Ta có :
4. Ta có : 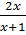 =
= 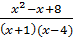 ⇒2x(x - 4) = x2 - x + 8 ⇔ 2x2 - 8x – x2 + x - 8 = 0 ⇔ x2 - 7x - 8 = 0.
x1 = -1, x2 = 8.
Vì x1 = -1 không thoả mãn điều kiện của ẩn nên loại.
Phương trình có một nghiệm là x2 = 8.
39. Giải: a) (3x2 -7x - 10)[2x2+(1 -
⇒2x(x - 4) = x2 - x + 8 ⇔ 2x2 - 8x – x2 + x - 8 = 0 ⇔ x2 - 7x - 8 = 0.
x1 = -1, x2 = 8.
Vì x1 = -1 không thoả mãn điều kiện của ẩn nên loại.
Phương trình có một nghiệm là x2 = 8.
39. Giải: a) (3x2 -7x - 10)[2x2+(1 - 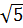 )x +
)x + 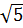 - 3] = 0
⇔
- 3] = 0
⇔ 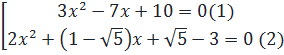 Giải(1) : x1 =-1, x2 =
Giải(1) : x1 =-1, x2 = 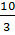 .
Giải (2): x3 = 1, x4 =
.
Giải (2): x3 = 1, x4 = 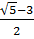 b) x3 + 3x2 - 2x - 6 = 0 ⇔ x2(x + 3) - 2(x + 3) = 0 ⇔ (x + 3)(x2 - 2) = 0
⇔
b) x3 + 3x2 - 2x - 6 = 0 ⇔ x2(x + 3) - 2(x + 3) = 0 ⇔ (x + 3)(x2 - 2) = 0
⇔ 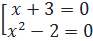 Vậy x1 = -3, x2=
Vậy x1 = -3, x2= 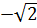 , x3 =
, x3 = 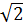 c) (x2 - 1)(0,6x + 1) = 0,6x2 + x ⇔ (0,6x + 1)(x2 - x - 1) = 0
⇔
c) (x2 - 1)(0,6x + 1) = 0,6x2 + x ⇔ (0,6x + 1)(x2 - x - 1) = 0
⇔ 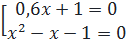 Vậy x1 =
Vậy x1 = 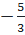 ; x2 =
; x2 = 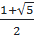 ; x3 =
; x3 = 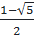 d) (x2 + 2x - 5)2 = (x2 - x + 5)2 ⇔ (x2 + 2x - 5)2 - (x2 - x + 5)2 = 0
⇔ (x2 + 2x - 5 + x2 - x + 5)(x2 + 2x – 5 – x2 + x - 5) = 0
⇔ (2x2 + x)(3x - 10) = 0 ⇔
d) (x2 + 2x - 5)2 = (x2 - x + 5)2 ⇔ (x2 + 2x - 5)2 - (x2 - x + 5)2 = 0
⇔ (x2 + 2x - 5 + x2 - x + 5)(x2 + 2x – 5 – x2 + x - 5) = 0
⇔ (2x2 + x)(3x - 10) = 0 ⇔ 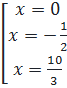 40. Hướng dẫn.
a) Đặt t = x2 + x, ta có phương trình 3t2 - 2t - 1 = 0. Giải phương trình này, ta tìm được hai giá trị của t. Thay mỗi giá trị của t vừa tìm được vào đẳng thức t = x2 + x, ta được một phương trình của ẩn x. Giải mỗi phương trình này sẽ tìm được giá trị của x.
Từ phương trình 3(x2 + x)2 - 2(x2 + x) - 1 = 0.
Đặt t = x2 + x, ta có : 3t2 - 2t - 1 = 0 ⇒ t1 = 1, t2 =
40. Hướng dẫn.
a) Đặt t = x2 + x, ta có phương trình 3t2 - 2t - 1 = 0. Giải phương trình này, ta tìm được hai giá trị của t. Thay mỗi giá trị của t vừa tìm được vào đẳng thức t = x2 + x, ta được một phương trình của ẩn x. Giải mỗi phương trình này sẽ tìm được giá trị của x.
Từ phương trình 3(x2 + x)2 - 2(x2 + x) - 1 = 0.
Đặt t = x2 + x, ta có : 3t2 - 2t - 1 = 0 ⇒ t1 = 1, t2 = 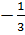 - Với t = 1, ta có : x2 + x = 1 hay x2 + x - 1 = 0, x1 =
- Với t = 1, ta có : x2 + x = 1 hay x2 + x - 1 = 0, x1 = 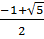 ; x2 =
; x2 = 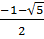 ;
Với t =
;
Với t = 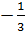 , ta có : x2 + x =
, ta có : x2 + x = 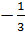 hay 3x2 + 3x + 1 = 0.
Phương trình này vô nghiệm.
Vậy phương trình đã cho có hai nghiệm : x1 =
hay 3x2 + 3x + 1 = 0.
Phương trình này vô nghiệm.
Vậy phương trình đã cho có hai nghiệm : x1 = 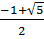 ; x2 =
; x2 = 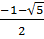 b) (x2 - 4x + 2)2 + x2 - 4x - 4 = 0.
Đặt t = x2 - 4x + 2 thì x2 - 4x = t - 2. Ta có phương trình t2 + t - 6 = 0.
Nghiệm của phượng trình là t1 = 2, t2 = -3.
Với t = 2, ta có : x2 - 4x + 2 = 2 hay x2 - 4x = 0. Suy ra x1 = 0, x2 = 4.
Với t = -3, ta có : x2 - 4x + 2 = -3 hay x2 - 4x + 5 = 0.
Phương trình này vô nghiệm.
Vậy phương trình đã cho có hai nghiệm x1 = 0, x2 = 4.
c) Điều kiện : x
b) (x2 - 4x + 2)2 + x2 - 4x - 4 = 0.
Đặt t = x2 - 4x + 2 thì x2 - 4x = t - 2. Ta có phương trình t2 + t - 6 = 0.
Nghiệm của phượng trình là t1 = 2, t2 = -3.
Với t = 2, ta có : x2 - 4x + 2 = 2 hay x2 - 4x = 0. Suy ra x1 = 0, x2 = 4.
Với t = -3, ta có : x2 - 4x + 2 = -3 hay x2 - 4x + 5 = 0.
Phương trình này vô nghiệm.
Vậy phương trình đã cho có hai nghiệm x1 = 0, x2 = 4.
c) Điều kiện : x 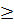 0. Ta có : x -
0. Ta có : x - 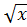 = 5
= 5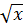 + 7 ⇔x - 6
+ 7 ⇔x - 6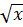 -7=0.
Đặt t =
-7=0.
Đặt t = 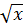 , t
, t 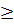 0, ta có : t2 - 6t -7 - 0. Suy ra : t1 = -1 (loại), t2 = 7.
Với t = 7, ta có :
0, ta có : t2 - 6t -7 - 0. Suy ra : t1 = -1 (loại), t2 = 7.
Với t = 7, ta có : 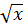 = 7. Suy ra x = 49.
Vậy phương trình đã cho có một nghiệm : x = 49.
d) Điều kiện : x
= 7. Suy ra x = 49.
Vậy phương trình đã cho có một nghiệm : x = 49.
d) Điều kiện : x 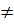 -1, x
-1, x 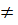 0.
0. 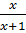 – 10 .
– 10 . 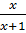 = 3
Đặt
= 3
Đặt 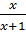 = t, ta có :
= t, ta có : 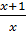 =
=  Vậy có phương trình t -
Vậy có phương trình t -  - 3 = 0 hay : t2 - 3t - 10 = 0.
Suy ra t1 = 5, t2 = -2.
- Với t = 5, ta có
- 3 = 0 hay : t2 - 3t - 10 = 0.
Suy ra t1 = 5, t2 = -2.
- Với t = 5, ta có 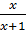 hay x = 5x + 5. Suy ra x =
hay x = 5x + 5. Suy ra x = 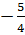 - Với t = -2, ta có
- Với t = -2, ta có 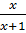 = -2 hay x = -2x - 2. Suy ra x =
= -2 hay x = -2x - 2. Suy ra x = 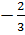 Vậy phương trình đã cho có hai nghiệm :x1 =
Vậy phương trình đã cho có hai nghiệm :x1 = 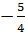 , x2 =
, x2 = 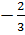 .
D. Bài tập luyện thêm
1. Giải phương trình :
a) x4 - 2x2 + 3 = 4x2 - 5 ;
b) 2x2 (x2 - 3) = x4 – x2 + 14.
2. Giải phương trình :
a)
.
D. Bài tập luyện thêm
1. Giải phương trình :
a) x4 - 2x2 + 3 = 4x2 - 5 ;
b) 2x2 (x2 - 3) = x4 – x2 + 14.
2. Giải phương trình :
a) 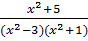 =
= 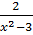 -
- 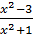 b)
b) 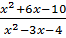 -
- 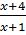 =
= 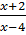 c)
c) 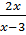 -
- 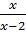 =
= 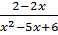 3. Giải phương trình :
a) 3x3 - 12x2 - 2x + 8 = 0 ;
b) (x2 - 3x + 1)2 = 3x2 - 9x+ 1.
Hướng dẫn - Đáp số
1. Đáp số:
a) x =
3. Giải phương trình :
a) 3x3 - 12x2 - 2x + 8 = 0 ;
b) (x2 - 3x + 1)2 = 3x2 - 9x+ 1.
Hướng dẫn - Đáp số
1. Đáp số:
a) x = 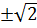 , x =
, x = 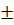 2 ; b) x =
2 ; b) x = 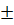
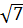 2. Giải: a) Điều kiện : x
2. Giải: a) Điều kiện : x 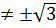
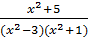 =
= 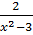 -
- 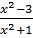 ⇒ x2 + 5 = 2(x2 + 1) – (x2 - 3)(x2 -3)
⇔ x2 + 5 = 2x2 + 2 – x4 + 6x2 – 9 ⇔ x4 – 7x2 + 12 = 0
Đặt t = x2; t
⇒ x2 + 5 = 2(x2 + 1) – (x2 - 3)(x2 -3)
⇔ x2 + 5 = 2x2 + 2 – x4 + 6x2 – 9 ⇔ x4 – 7x2 + 12 = 0
Đặt t = x2; t 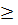 0, ta có: t2 – 7t + 12 = 0
0, ta có: t2 – 7t + 12 = 0
 = 49 – 4.1.12 = 1
t1 =
= 49 – 4.1.12 = 1
t1 = 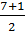 = 4 ; t2 =
= 4 ; t2 = 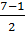 = 3
- Với t = 4; ta có: x2 = 4; suy ra: x =
= 3
- Với t = 4; ta có: x2 = 4; suy ra: x =  2
- Với t = 3; ta có: x2 = 3; suy ra: x =
2
- Với t = 3; ta có: x2 = 3; suy ra: x = 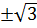 Vì x =
Vì x = 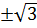 không thỏa mãn điều kiện nên phương trình có hai nghiệm: x =
không thỏa mãn điều kiện nên phương trình có hai nghiệm: x = 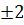 b) Điều kiện: x
b) Điều kiện: x 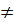 -1; x
-1; x 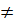 4
4
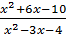 -
- 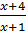 =
= 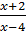 ⇒ x2 + 6x -10 – (x + 4)(x - 4) = (x+2)(x +1)
⇔ x2 + 6x -10 – x2 + 16 = x2 + 3x + 2 ⇔ x2 – 3x – 4 = 0
Vì: 1+3 – 4 =0 nên x = -1 (loại); x = 4 (loại)
Phương trình vô nghiệm.
c) Điều kiện: x
⇒ x2 + 6x -10 – (x + 4)(x - 4) = (x+2)(x +1)
⇔ x2 + 6x -10 – x2 + 16 = x2 + 3x + 2 ⇔ x2 – 3x – 4 = 0
Vì: 1+3 – 4 =0 nên x = -1 (loại); x = 4 (loại)
Phương trình vô nghiệm.
c) Điều kiện: x 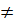 2; x
2; x 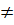 3
3
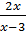 -
- 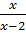 =
= 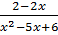 ⇒ 2x(x-2) – x (x - 3) = 2 – 2x
⇔ 2x2 – 4x – x2 + 3x = 2 – 2x ⇔ x2 + x – 2 = 0
Vì phương trình có 1 + 1 – 2 = 0 nên x1 =1; x2 = -2
Hai giá trị tìm được của x đều thỏa mãn điều kiện của ẩn nên phương trình có hai nghiệm là: x1 =1; x2 = -2
3. Giải: a) 3x3 - 12x2 - 2x + 8 = 0 ⇔ 3x2 (x - 4) - 2(x - 4) = 0
⇔ (x - 4)(3x2 - 2) = 0 ⇔
⇒ 2x(x-2) – x (x - 3) = 2 – 2x
⇔ 2x2 – 4x – x2 + 3x = 2 – 2x ⇔ x2 + x – 2 = 0
Vì phương trình có 1 + 1 – 2 = 0 nên x1 =1; x2 = -2
Hai giá trị tìm được của x đều thỏa mãn điều kiện của ẩn nên phương trình có hai nghiệm là: x1 =1; x2 = -2
3. Giải: a) 3x3 - 12x2 - 2x + 8 = 0 ⇔ 3x2 (x - 4) - 2(x - 4) = 0
⇔ (x - 4)(3x2 - 2) = 0 ⇔ 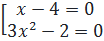 ⇔
⇔ 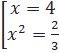 ⇔
⇔ 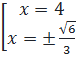 b) (x2 - 3x + 1)2 = 3x2 - 9x + 1 (x2 - 3x + 1)2 = 3(x2 - 3x + 1) - 2
⇔ (x2 - 3x + 1)2 - 3(x2 - 3x + 1) + 2 = 0.
Đặt t = x2 - 3x + 1, ta có : t2 - 3t + 2 = 0
- Với t = 1, ta có x2 - 3x + 1 = 1 ⇔ x2 - 3x = 0 ⇔ x(x - 3) = 0 ⇔
b) (x2 - 3x + 1)2 = 3x2 - 9x + 1 (x2 - 3x + 1)2 = 3(x2 - 3x + 1) - 2
⇔ (x2 - 3x + 1)2 - 3(x2 - 3x + 1) + 2 = 0.
Đặt t = x2 - 3x + 1, ta có : t2 - 3t + 2 = 0
- Với t = 1, ta có x2 - 3x + 1 = 1 ⇔ x2 - 3x = 0 ⇔ x(x - 3) = 0 ⇔ 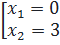 - Với t = 2, ta có x2 - 3x + 1 = 2 ⇔ x2 - 3x – 1 = 0.
- Với t = 2, ta có x2 - 3x + 1 = 2 ⇔ x2 - 3x – 1 = 0.
 = 9 – 4.1.(-1) = 13. Ta có: x3 =
= 9 – 4.1.(-1) = 13. Ta có: x3 =  ; x4 =
; x4 = 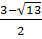 Vậy phương trình có bốn nghiệm x1 = 0, x2 = 3, x3 =
Vậy phương trình có bốn nghiệm x1 = 0, x2 = 3, x3 = 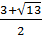 ; x4 =
; x4 = 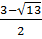
© Bản quyền thuộc về
Bài kiểm tra. Ghi rõ nguồn Bài kiểm tra.com khi sao chép nội dung này.
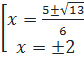
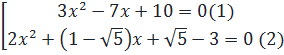
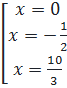
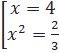 ⇔
⇔