Giải bài tập Hình học 9, chương III, bài 3: Góc nội tiếp
2019-08-28T04:51:27-04:00
2019-08-28T04:51:27-04:00
Giải bài tập Hình học 9, chương III, bài 3: Góc nội tiếp: Tóm tắt kiến thức, ví dụ, hướng dẫn giải bài tập trong sách giáo khoa và bài tập luyện thêm.
/themes/cafe/images/no_image.gif
Bài Kiểm Tra
https://baikiemtra.com/uploads/bai-kiem-tra-logo.png
Thứ tư - 28/08/2019 04:39
Giải bài tập Hình học 9, chương III, bài 3: Góc nội tiếp: Tóm tắt kiến thức, ví dụ, hướng dẫn giải bài tập trong sách giáo khoa và bài tập luyện thêm.
A. Tóm tắt kiến thức
1. Định nghĩa
Góc nội tiếp là góc có đỉnh nằm bên trên đường tròn và hai cạnh chứa hai dây cung của đường tròn đó (h.30).
2. Định lí
Trong một đường tròn, số đo của góc nội tiếp bằng nửa số đo của cung bị chắn.
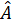 = =  sđ sđ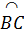 . . |
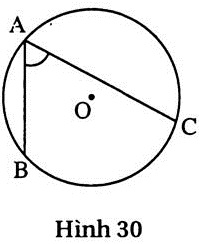 |
3. Hệ quả
Trong một đường tròn :
a) Các góc nội tiếp bằng nhau chắn các cung bằng nhau.
b) Các góc nội tiếp cùng chắn một cung hoặc chắn các bằng nhau.
c) Góc nội tiếp (nhỏ hơn hoặc bằng 90o) có số đo bằng nửa số đo của góc ở tâm cùng chắn một cung.
d) Góc nội tiếp chắn nửa đường tròn là góc vuông.
B. Ví dụ
Cho đường tròn (O) dây AB. Gọi C là, điểm chính giữa của cung nhỏ AB. Vẽ dây CD bất kì cắt AB tại M.
a) Chứng minh rằng tích CM.CD không đổi.
b) Vẽ đường tròn (K) ngoại tiếp tam giác AMD. Chứng minh rằng 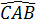 =
= 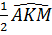 .
c) Chứng minh rằng AC là tiếp tuyến của đường tròn (K).
d) Vẽ đường kính COE. Chứng minh ba điểm A, K, E thẳng hàng.
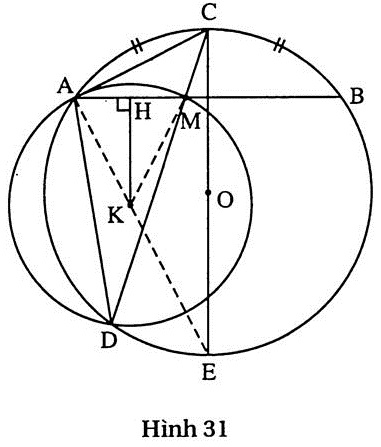
Giải (h.31)
.
c) Chứng minh rằng AC là tiếp tuyến của đường tròn (K).
d) Vẽ đường kính COE. Chứng minh ba điểm A, K, E thẳng hàng.
Giải (h.31)
a)  CAM và CAM và  CDA có : CDA có : 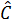 chung ; chung ; 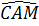 = = 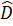 (vì hai góc nội tiếp cùng chắn hai cung bằng nhau). (vì hai góc nội tiếp cùng chắn hai cung bằng nhau).
Do đó  CAM CAM 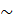  CDA (g.g). CDA (g.g).
Suy ra 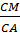 = = 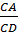 ⇒ CM.CD = CA2 (không đổi). ⇒ CM.CD = CA2 (không đổi).
b) Xét đường tròn (K) ta có 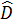 = = 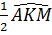 (góc nội tiếp bằng nửa góc ở tâm cùng chắn cung AM). (góc nội tiếp bằng nửa góc ở tâm cùng chắn cung AM).
Mặt khác 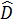 = = 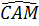 (chứng minh trên) (chứng minh trên)
nên 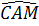 = = 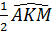 . .
c) Vẽ KH ⊥ AM thì 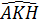 = = 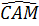 (= (= 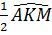 ). ).
Xét  AKH vuông tại H, ta có : AKH vuông tại H, ta có :
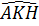 + + 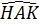 = 90o, suy ra = 90o, suy ra 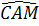 + + 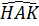 = 90o. = 90o.
Do đó AK ⊥ AC, dẫn tới CA là tiếp tuyến của đường tròn (K).
d) Ta có 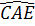 = 90o (góc nội tiếp chắn nửa đường tròn). Suy ra AE ⊥ AC. Mặt khác AK ⊥ AC nên hai tia AE và AK trùng nhau. Do đó ba điểm A, K, E thẳng hàng. = 90o (góc nội tiếp chắn nửa đường tròn). Suy ra AE ⊥ AC. Mặt khác AK ⊥ AC nên hai tia AE và AK trùng nhau. Do đó ba điểm A, K, E thẳng hàng. |
 |
Nhận xét: Ở câu c) ta đã chứng minh AC là tiếp tuyến theo dấu hiệu nhận biết đã học. Ngoài cách này, còn có thể chứng minh theo cách khác sau khi học §4.
C. Hướng dẫn giải bài tập trong sách giáo khoa
15. Trả lời: a) Đúng ; b) Sai.
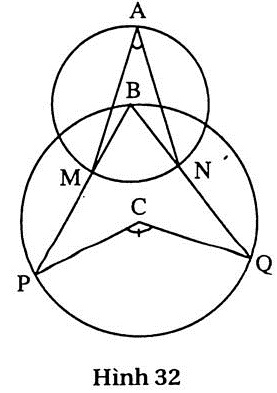
16. Hướng dẫn (h.32)
a) 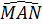 = 30o ⇒ = 30o ⇒ 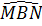 = 60o ⇒ = 60o ⇒ 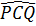 = 120o. = 120o.
b) 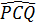 = 136o ⇒ = 136o ⇒ 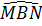 = 68o ⇒ = 68o ⇒ 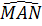 = 34o. = 34o. |
|
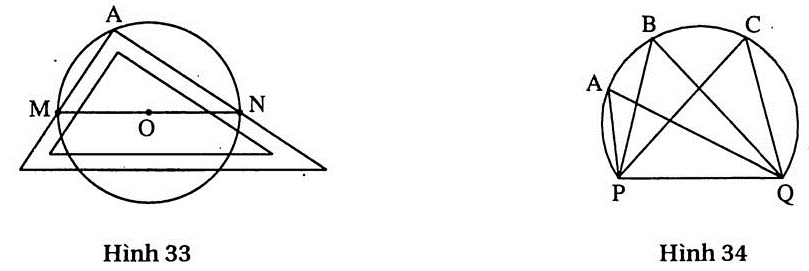
17. Giải (h.33)
- Đặt êke sao cho đỉnh góc vuông A của nó nằm trên đường tròn hai cạnh góc vuông (hai mép ngoài) cắt đường tròn tại M và N. Vẽ đoạn thẳng MN ta được một đường kính của đường tròn.
- Làm tương tự như trên để có một đường kính thứ hai.
- Giao điểm của hai đường kính là tâm của đường tròn.
18. Trả lời: 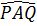 =
= 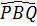 =
= 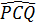 (h.34) (các góc nội tiếp cùng chắn cung PQ).
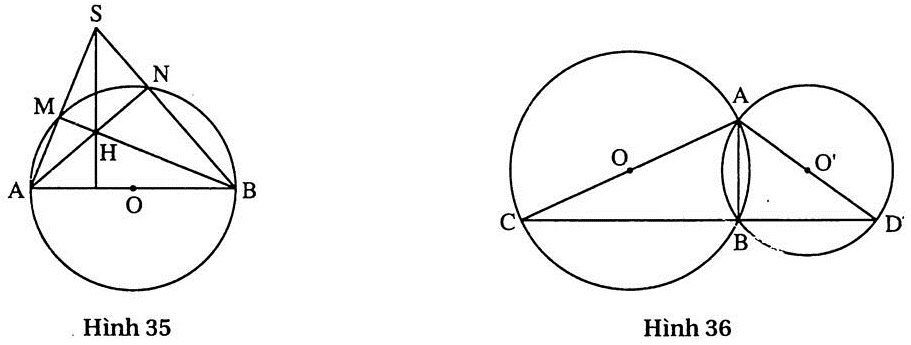
19. Giải (h.35)
Ta có:
(h.34) (các góc nội tiếp cùng chắn cung PQ).
19. Giải (h.35)
Ta có: 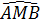 =
= 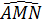 = 90o (góc nội tiếp chắn nửa đường tròn).
Do đó: AN ⊥ SB ; BM ⊥ SA. Xét
= 90o (góc nội tiếp chắn nửa đường tròn).
Do đó: AN ⊥ SB ; BM ⊥ SA. Xét  SAB có H là trực tâm, suy ra SH ⊥ AB.
20. Giải (h.36)
Vẽ các dây BC, BD và BA.
Ta có
SAB có H là trực tâm, suy ra SH ⊥ AB.
20. Giải (h.36)
Vẽ các dây BC, BD và BA.
Ta có 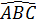 =
= 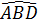 = 90o (góc nội tiếp chắn nửa đường tròn).
Do đó BC ⊥ BA ; BD ⊥ BA. Qua điểm B chỉ vẽ được một đường thẳng vuông góc với BA, suy ra ba điểm C, B, D thẳng hàng.
= 90o (góc nội tiếp chắn nửa đường tròn).
Do đó BC ⊥ BA ; BD ⊥ BA. Qua điểm B chỉ vẽ được một đường thẳng vuông góc với BA, suy ra ba điểm C, B, D thẳng hàng.
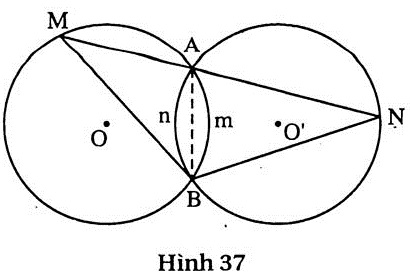
21. Giải (h.37)
Vì hai đường tròn (O) và (O’) bằng nhau nên 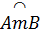 = = 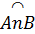 (cùng căng dây AB). (cùng căng dây AB).
Suy ra 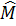 = = 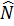 (hai góc nội tiếp chắn hai cung bằng nhau). Do đó (hai góc nội tiếp chắn hai cung bằng nhau). Do đó  BMN là tam giác cân. BMN là tam giác cân.
Cảnh báo! Nếu hai đường tròn (O) và (O’) không bằng nhau thì các cung AmB và AnB không bằng nhau mặc dù chúng cùng căng một dây. |
|
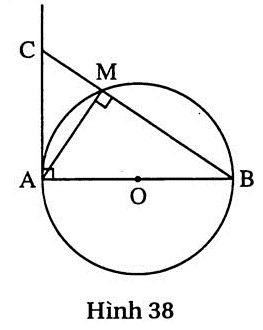
22. Hướng dẫn (h.38)
Áp dụng hệ thức h2 = b’c’ đối với tam giác vuông ABC. |
|
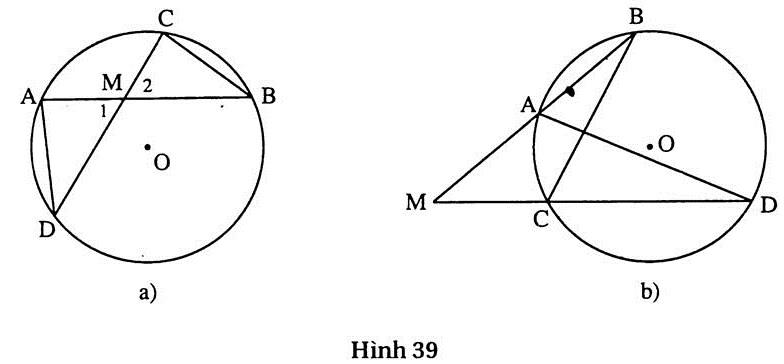
23. Hướng dẫn. Xét cả hai trường hợp điểm M nằm bên trong và bên ngoài đường tròn. Trong mỗi trường hợp, xét hai tam giác đồng dạng.
- Trường hợp điểm M nằm bên trong đường tròn (h.39a)
Xét  MAD và
MAD và  MBC, ta có :
MBC, ta có :
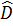 =
= 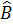 (hai góc nội tiếp cùng chắn cung AC),
(hai góc nội tiếp cùng chắn cung AC),
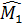 =
= 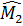 (đối đỉnh).
Vậy
(đối đỉnh).
Vậy  MAD
MAD 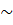
 MCB (g.c).
Suy ra:
MCB (g.c).
Suy ra: 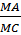 =
= 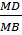 do đó MA.MB = MC.MD.
- Trường hợp điểm M nằm bên ngoài đường tròn (h.39b) cũng chứng minh tương tự.
do đó MA.MB = MC.MD.
- Trường hợp điểm M nằm bên ngoài đường tròn (h.39b) cũng chứng minh tương tự.
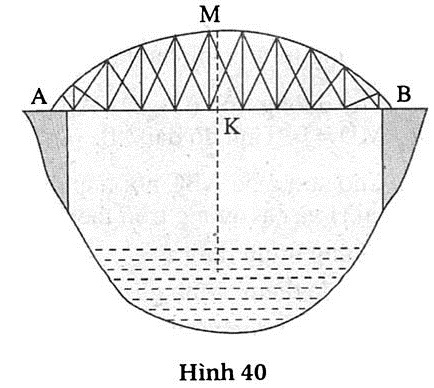
24. Giải (h.40)
Vẽ đường kính MON của đường tròn chứa cung AMB. Ta đặt MN = 2R thì KN = 2R - 3.
Theo Bài 23 ta có
KA.KB = KM.KN
hay KA.KB = KM.(2R - 3).
Thay số : 20.20 = 3.(2R - 3) ⇒ R = 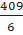 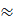 68,2 (m) 68,2 (m) |
|
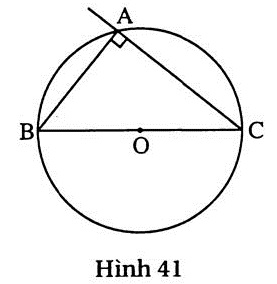
25. Hướng dẫn (h.41)
- Dựng đường tròn (O) đường kính BC = 4cm.
- Dựng cung tròn (B ; 2,5cm) cắt đường tròn (O) tại A.
- Nối AB, AC ta được  ABC phải dựng. Bạn đọc giải tiếp các bước còn lại. ABC phải dựng. Bạn đọc giải tiếp các bước còn lại. |
|
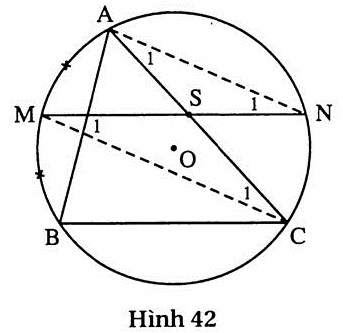
26. Giải (h.42)
Ta có MN // BC, suy ra 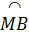 = = 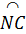 . .
Mặt khác 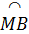 = = 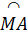 nên nên 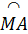 = = 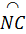 . .
Ta có 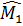 = = 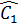 và và 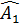 = = 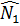 (hai góc nội tiếp chắn hai cung bằng nhau). (hai góc nội tiếp chắn hai cung bằng nhau).
Do đó  SMC và SMC và  SAN là những tam giác cân. SAN là những tam giác cân.
Suy ra SM = SC, SA = SN. |
|
D. Bài tập luyện thêm
1. Cho tam giác ABC nội tiếp đường tròn (O). Vẽ các bán kính OD ⊥ BC, OE ⊥ AC, OF ⊥ AB?
Chứng minh rằng ba đường thẳng AD, BE, CF đồng quy.
2. Cho đường tròn (O), dây AB. Vẽ OM ⊥ AB. Qua M vẽ dây CD. Giả sử MC = 4, MD = 9. Tính độ dài AB.
3. Cho tam giác ABC nội tiếp đường tròn (O). Các đường cao BD và CE cắt nhau tại H và cắt đường tròn theo thứ tự tại F và G.
Chứng minh rằng :
a) A là điểm chính giữa của cung GF.
b) F đối xứng với H qua AC, G đối xứng với H qua AB.
c) OA ⊥ DE.
4. Cho tam giác ABC nội tiếp đường tròn (O), góc A nhọn, cạnh BC cố định. Gọi K là tâm đường tròn nội tiếp  ABC. Khi điểm A di động trên cung lớn BC, chứng minh rằng :
a) Đường thẳng AK luôn đi qua một điểm cố định.
b) Điểm K di động trên một đường tròn cố định.
c) Cho hai đường tròn (O ; R) và (O’; R’) cắt nhau tại A và B. Vẽ các đường kính AOC và AO’D.
a) Chứng minh ba điểm C, B, D thẳng hàng.
b) Qua B vẽ một đường thẳng cắt đường tròn (O) và (O’) lần lượt tại M và N. Chứng minh rằng
ABC. Khi điểm A di động trên cung lớn BC, chứng minh rằng :
a) Đường thẳng AK luôn đi qua một điểm cố định.
b) Điểm K di động trên một đường tròn cố định.
c) Cho hai đường tròn (O ; R) và (O’; R’) cắt nhau tại A và B. Vẽ các đường kính AOC và AO’D.
a) Chứng minh ba điểm C, B, D thẳng hàng.
b) Qua B vẽ một đường thẳng cắt đường tròn (O) và (O’) lần lượt tại M và N. Chứng minh rằng  AMN
AMN 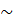
 ACD.
c) Cho biết '
ACD.
c) Cho biết '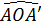 = 120o. Tính diện tích lớn nhất của tam giác AMN.
Hướng dẫn - đáp số
= 120o. Tính diện tích lớn nhất của tam giác AMN.
Hướng dẫn - đáp số
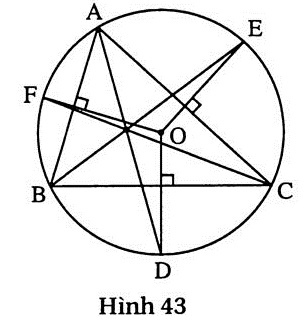
1. (h.43). Ta có OD ⊥ BC, suy ra 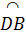 = = 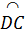 , do đó , do đó 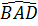 = = 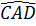 . Vậy AD là tia phân giác của góc A. Chứng minh tương tự ta được BE, CF theo thứ tự là các tia phân giác của góc B, góc C. . Vậy AD là tia phân giác của góc A. Chứng minh tương tự ta được BE, CF theo thứ tự là các tia phân giác của góc B, góc C.
Ba đường thẳng AD, BE, CF là ba đường phân giác của AABC nên chúng đồng quy. |
|
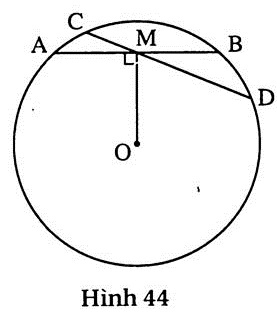
2. (h.44). Vì OM ⊥ AB nên MA = MB.
Ta có MA.MB = MC.MD (xem bài 23).
Do đó MA2 = 4.9 = 36, suy ra MA = 6, dẫn tới AB= 12. |
|
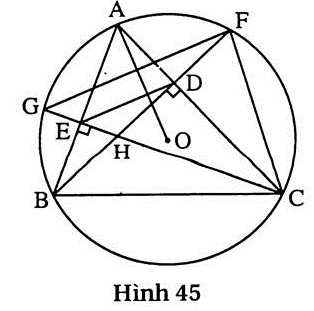
3. (h.45)
a) Ta có 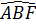 = = 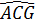 (cùng phụ với góc A). (cùng phụ với góc A).
Suy ra 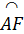 = = 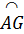 (hai góc nội tiếp bằng nhau thì hai cung bị chắn bằng nhau). (hai góc nội tiếp bằng nhau thì hai cung bị chắn bằng nhau).
b) Ta có  CDF = CDF =  CDH (g.c.g). Suy ra DF = DH. CDH (g.c.g). Suy ra DF = DH.
Mặt khác HF ⊥ AC nên F và H đối xứng với nhau qua AC.
Chứng minh tương tự ta được G và H đối xứng với nhau qua AB.
c) Xét  HGF có DE là đường trung bình nên DE // GF. Vì HGF có DE là đường trung bình nên DE // GF. Vì 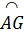 = = 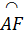 nên OA ⊥ GF, do đó OA ⊥ DE nên OA ⊥ GF, do đó OA ⊥ DE
|
|
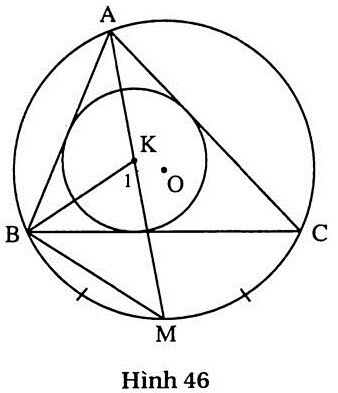
4. (h.46)
a) Tia AK cắt đường tròn (O) tại một điểm thứ hai là M.
Vì 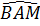 = = 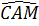 nên nên 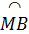 = = 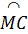
Vậy đường thẳng AK luôn đi qua một điểm cố định là điểm chính giữa M của cung BC.
b) Ta có 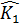 = = 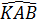 + + 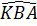 , ,
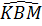 = = 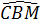 + + 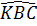 . .
Mặt khác 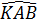 = = 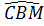 (hai góc nội tiếp chắn hai cung bằng nhau). (hai góc nội tiếp chắn hai cung bằng nhau).
Ta lại có 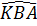 = = 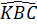 (vì tia BK là tia phân giác của góc ABC). Do đó Kị = KBM. Vậy AMBK cân, suy ra MK = MB. Điểm K cách điểm M cho trước một khoảng bằng MB nên K (vì tia BK là tia phân giác của góc ABC). Do đó Kị = KBM. Vậy AMBK cân, suy ra MK = MB. Điểm K cách điểm M cho trước một khoảng bằng MB nên K 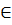 (M ; MB). (M ; MB). |
|
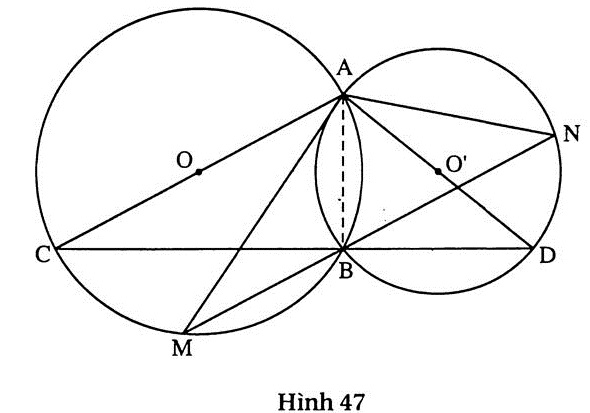
5. (h. 47)
a) Xem cách giải bài 20
b) Ta có 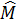 =
= 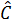 ;
; 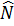 =
= 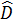 (hai góc nội tiếp cùng chắn một cung).
Do đó
(hai góc nội tiếp cùng chắn một cung).
Do đó  AMN
AMN 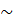
 ACD.
c) Ta có
ACD.
c) Ta có 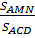 =
= 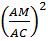 . vì AM
. vì AM 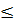 AC (sự liên hệ giữa dây và đường kính)
nên:
AC (sự liên hệ giữa dây và đường kính)
nên: 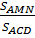
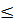 1 (dấu “=” xảy ra ⇔ M
1 (dấu “=” xảy ra ⇔ M 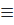 C và N
C và N 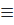 D)
Do đó max
D)
Do đó max 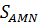 =
= 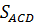 =
=  AC.ADsin60o =
AC.ADsin60o =  .2R.2R’.
.2R.2R’.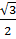 =
= 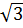 RR’.
RR’.
© Bản quyền thuộc về
Bài kiểm tra. Ghi rõ nguồn Bài kiểm tra.com khi sao chép nội dung này.