Giải bài tập Hình học 9, chương III, bài 9: Độ dài đường tròn, cung tròn
2019-08-30T05:17:55-04:00
2019-08-30T05:17:55-04:00
Giải bài tập Hình học 9, chương III, bài 9: Độ dài đường tròn, cung tròn: Tóm tắt kiến thức, ví dụ, hướng dẫn giải bài tập trong sách giáo khoa và bài tập luyện thêm.
/themes/cafe/images/no_image.gif
Bài Kiểm Tra
https://baikiemtra.com/uploads/bai-kiem-tra-logo.png
Thứ sáu - 30/08/2019 05:15
Giải bài tập Hình học 9, chương III, bài 9: Độ dài đường tròn, cung tròn: Tóm tắt kiến thức, ví dụ, hướng dẫn giải bài tập trong sách giáo khoa và bài tập luyện thêm.
A. Tóm tắt kiến thức
1. Công thức tính độ dài đường tròn
C = 2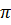 R hoặc C =
R hoặc C = 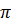 d
trong đó R là bán kính ; d là dường kính.
2. Công thức tính độ dài cung tròn
l =
d
trong đó R là bán kính ; d là dường kính.
2. Công thức tính độ dài cung tròn
l = 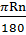 (R là bán kính, n là số đo cung).
B. Ví dụ
Hình chữ nhật ABCD có AB = 2
(R là bán kính, n là số đo cung).
B. Ví dụ
Hình chữ nhật ABCD có AB = 2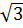 cm ; BC = 2cm.
a) Tính chu vi của đường tròn ngoại tiếp hình chữ nhật.
b) Tính độ dài cung nhỏ BC.
cm ; BC = 2cm.
a) Tính chu vi của đường tròn ngoại tiếp hình chữ nhật.
b) Tính độ dài cung nhỏ BC.
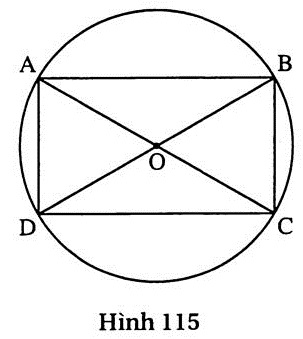
Giải (h. 115)
a) Trong hình chữ nhật, giao điểm O của hai đường chéo là tâm của đường tròn ngoại tiếp.
Ta có AC2 = AB2 + BC2 = (2 ) + 22. ) + 22.
Vậy AC2 = 16, suy ra AC = 4 (cm).
Vậy bán kính đường tròn ngoại tiếp là R = 2cm.
Chu vi đường tròn ngoại tiếp là :
C = 2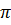 R = R = 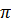 .4 = 4 .4 = 4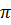 (cm). (cm). |
|
b) Tam giác BOC có ba cạnh bằng nhau nên là tam giác đều, do đó 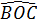 = 60o, sđ
= 60o, sđ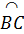 = 60o.
Độ dài cung nhỏ BC là :
l =
= 60o.
Độ dài cung nhỏ BC là :
l = 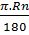 =
= 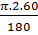 =
= 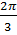 (cm)
Nhận xét:
- Để tính được độ dài của một đường tròn, yếu tố duy nhất cần xác định là bán kính R.
- Để tính được độ dài cung tròn, ngoài bán kính của đường tròn ta cần biết thêm số đo của cung tròn đó.
C. Hướng dẫn giải bài tập trong sách giáo khoa
65. Đáp số:
(cm)
Nhận xét:
- Để tính được độ dài của một đường tròn, yếu tố duy nhất cần xác định là bán kính R.
- Để tính được độ dài cung tròn, ngoài bán kính của đường tròn ta cần biết thêm số đo của cung tròn đó.
C. Hướng dẫn giải bài tập trong sách giáo khoa
65. Đáp số:
Cột 1 : 20 ; 62,80 ;
Cột 3 : 6; 18,84;
Cột 5 : 3,18 ; 6,37 ; |
Cột 2 : 5 ; 31,40.
Cột 4: 1,50; 9,42.
Cột 6 : 4 ; 8. |
66. Đáp số:
a) 2,09dm ; b) 2041mm.
67. Đáp số:
Cột 1 : 15,7cm ;
Cột 3 : 57° ;
Cột 5 : 21,1cm. |
Cột 2 : 40,8cm ;
Cột 4 : 4,4cm ; |
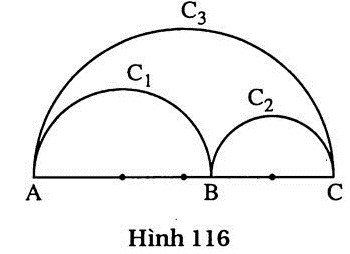
68. Giải (h. 116)
Ta đặt AB = 2a ; BC = 2b thì AC = 2(a + b).
Độ dài nửa đường tròn đường kính AB là :
C1 = 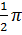 .2a = .2a = 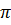 a. (1) a. (1)
Độ dài nửa đường tròn đường kính BC là :
C2 = 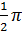 .2b = .2b = 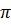 b. (2) b. (2)
Độ dài nửa đường tròn đường kính AC là :
C3 = 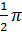 .2(a + b) = .2(a + b) = 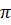 (a + b) = (a + b) = 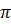 a + a + 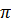 b b
Từ(1), (2), (3)suy ra C1+ C2 = C3 |
|
Nhận xét: Việc đặt AB = 2a ; BC = 2b làm cho biểu thức tính độ dài các nửa đường tròn được gọn gàng hơn là đặt AB = a, BC = b.
69. Hướng dẫn: 
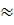 19(vòng).
70. Hướng dẫn:
+ Cách vẽ các hình :
- Vẽ hình vuông cạnh 4cm
- Vẽ hai đoạn thẳng nối trung điểm các cặp cạnh đối diện
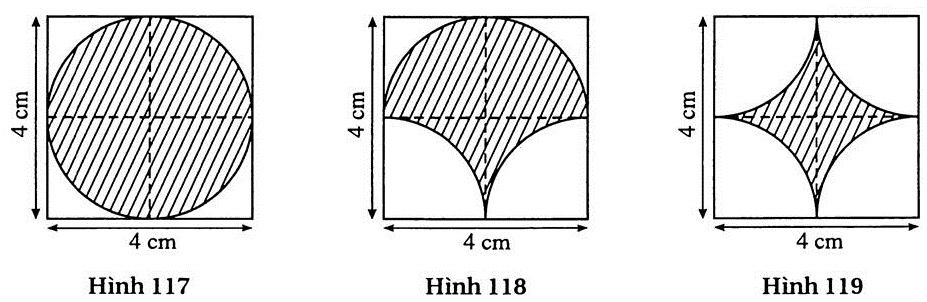
Hình 117: Vẽ đường tròn có tâm là tâm hình vuông, bán kính 2cm.
Hình 118 : Vẽ nửa đường tròn có tâm là tâm hình vuông, bán kính 2cm. Vẽ tiếp hai cung “phần tư” có tâm là hai đỉnh hình vuông và cùng bán kính 2cm.
Hình 119 : Vẽ bốn cung “phần tư” có tâm là bốn đỉnh hình vuông, bán kính 2cm.
+ Tính chu vi mỗi hình :
Mỗi hình gồm bốn cung “phần tư” ghép lại thành một đường tròn có đường kính 4cm.
Chu vi của mỗi hình là : C =
19(vòng).
70. Hướng dẫn:
+ Cách vẽ các hình :
- Vẽ hình vuông cạnh 4cm
- Vẽ hai đoạn thẳng nối trung điểm các cặp cạnh đối diện
Hình 117: Vẽ đường tròn có tâm là tâm hình vuông, bán kính 2cm.
Hình 118 : Vẽ nửa đường tròn có tâm là tâm hình vuông, bán kính 2cm. Vẽ tiếp hai cung “phần tư” có tâm là hai đỉnh hình vuông và cùng bán kính 2cm.
Hình 119 : Vẽ bốn cung “phần tư” có tâm là bốn đỉnh hình vuông, bán kính 2cm.
+ Tính chu vi mỗi hình :
Mỗi hình gồm bốn cung “phần tư” ghép lại thành một đường tròn có đường kính 4cm.
Chu vi của mỗi hình là : C = 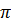 .4
.4 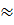 12,56 (cm).
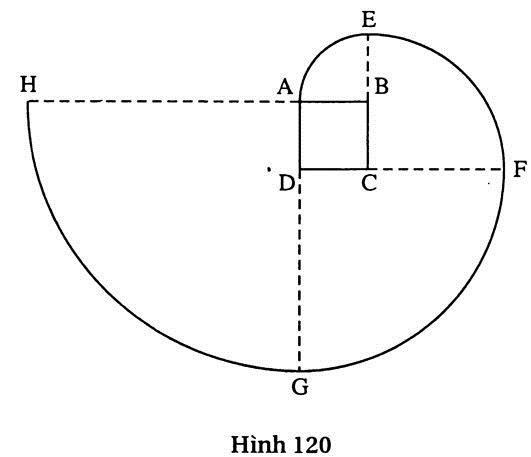
71. Hướng dẫn (h.120) :
Độ dài đường xoắn AEFGH là :
l =
12,56 (cm).
71. Hướng dẫn (h.120) :
Độ dài đường xoắn AEFGH là :
l =  .2
.2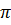 ( 1 + 2 + 3 + 4) = 5
( 1 + 2 + 3 + 4) = 5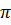 (cm).
(cm).
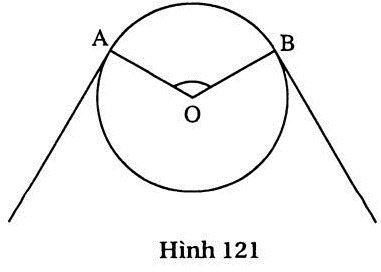
72. Giải (h. 121)
Ta có l = 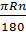 = = 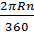
Thay số : 200 = 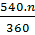 ⇒ n = ⇒ n = 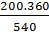 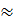 133 133
Vậy 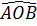 = sđ = sđ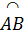 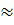 133o. 133o. |
|
73. Hướng dẫn
Từ công thức C = 2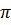 R, suy ra R =
R, suy ra R = 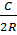 Đáp số: 6369km.
Đáp số: 6369km.
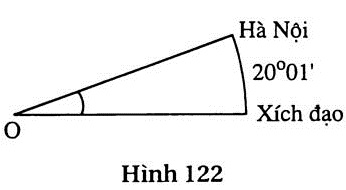
74. Giải: (h.122)
Vĩ độ của Hà Nội là 20o01’ có nghĩa là cung kinh tuyến từ xích đạo đến Hà Nội có số đo là: 20o01’ = 20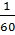 độ. độ.
Độ dài của cung đó là:
l = 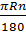 = = 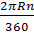 = = 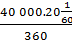 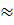 2224 (km) 2224 (km) |
|
Nhận xét: Trong công thức 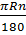 có
có 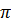 R là độ dài của một nửa đường tròn. Trong đề bài có cho độ dài của cả đường tròn nên ta biến đổi
R là độ dài của một nửa đường tròn. Trong đề bài có cho độ dài của cả đường tròn nên ta biến đổi 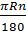 =
= 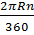 để có điều kiện thay thế 2
để có điều kiện thay thế 2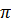 R = 40 000km.
R = 40 000km.
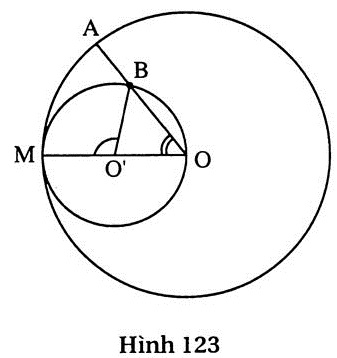
75. Giải (h. 123)
Xét đường tròn (O’) ta có 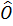 = = 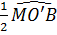 (quan hệ giữa góc nội tiếp và góc ở tâm). (quan hệ giữa góc nội tiếp và góc ở tâm).
Ta đặt 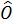 = no thì = no thì 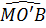 = 2no . Suy ra sđ = 2no . Suy ra sđ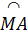 = no ; sđ = no ; sđ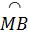 = 2no. = 2no.
Ta có 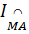 = = 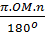 (1) (1)
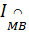 = = 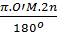 = = 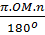 (2) (2)
Từ (1) và (2) suy ra: 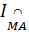 = = 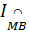 |
|
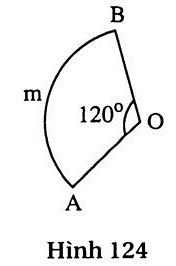
76. Giải (h.124)
Gọi bán kính của cung tròn là R. Ta có
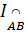 = =  = 2R. = 2R. > 2R (1) (vì > 2R (1) (vì  > 1) > 1)
Độ dài của đường gấp khúc AOB là
l = R + R = 2R. (2)
Từ (1) và (2) suy ra 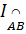 > l > l |
|
D. Bài tập luyện thêm
1. Cho hình thoi ABCD có AB = AO = 3cm. Vẽ đường tròn ngoại tiếp tam giác ABC.
a) Tính độ dài của đường tròn này.
b) Tính độ dài của cung BAC.
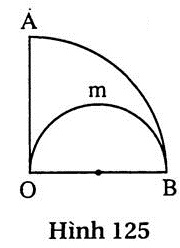
| 2. So sánh độ dài của cung OmB với độ dài của cung AB (h.125). |
|
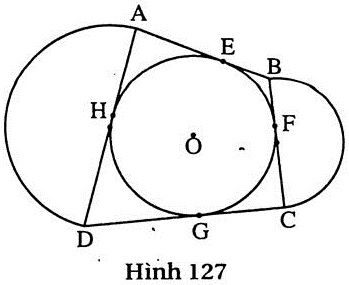
3. Tứ giác ABCD ngoại tiếp đường tròn (O). Vẽ các nửa đường tròn đường kính AD và BC ra phía ngoài của tứ giác. Biết AB + CD = 10cm. Tính tổng các độ dài của hai nửa đường tròn này.
Hướng dẫn - Đáp số
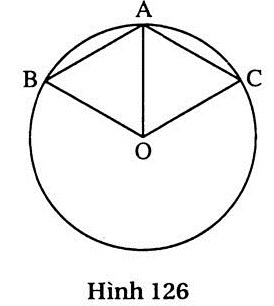
1. (h.126).
a) Ta có OB = OC = AB = AO = 3cm. Do đó đường tròn ngoại tiếp  ABC là đường tròn (O ; 3cm). Độ dài đường tròn này là : C = 2 ABC là đường tròn (O ; 3cm). Độ dài đường tròn này là : C = 2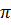 .R = 6 .R = 6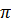 (cm). (cm).
b) Tam giác AOB, AOC đều.
Do đó 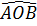 = =  = 60o, suy ra = 60o, suy ra 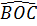 = 120o, = 120o, 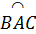 = 120o. = 120o.
Độ dài của cung BAC là :
l = 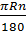 = =  = 2 = 2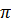 (cm) (cm) |
|
2. Ta đặt OA = OB = 2a.
Độ dài của cung OmB là :
l1 =  .
.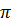 .2a =
.2a = 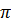 a (cm)
Độ dài của cung AB là:
l2 =
a (cm)
Độ dài của cung AB là:
l2 =  .
.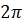 .2a =
.2a = 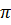 a (cm)
Vậy: l1 = l2
a (cm)
Vậy: l1 = l2
3. (h.127) Gọi E, F, G, H lần lượt là các tiếp điểm của đường tròn (O) với các cạnh AB, BC, CD, DA. Ta có: AH = AE; DH = DG; BF = BE; CF = CG
Do đó AD + BC = AB + CD = 10cm |
|
Tổng độ dài của hai nửa đường tròn đường kính AD và BC là :
C =  .
.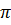 .AD +
.AD +  .
.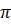 .BC =
.BC =  .
.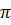 ( AD + BC) =
( AD + BC) =  .
.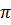 .10 = 5
.10 = 5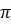 (cm).
Nhận xét: Qua bài giải trên ta thấy một tính chất của tứ giác ngoại tiếp là : Tổng các cặp cạnh đối diện bằng nhau.
(cm).
Nhận xét: Qua bài giải trên ta thấy một tính chất của tứ giác ngoại tiếp là : Tổng các cặp cạnh đối diện bằng nhau.
© Bản quyền thuộc về
Bài kiểm tra. Ghi rõ nguồn Bài kiểm tra.com khi sao chép nội dung này.