Giải bài tập Toán 9, chương I: bài 3: Liên hệ giữa phép nhân và phép khai phương
2019-07-30T04:35:02-04:00
2019-07-30T04:35:02-04:00
Giải bài tập Toán 9, chương I: bài 3: Liên hệ giữa phép nhân và phép khai phương
/themes/cafe/images/no_image.gif
Bài Kiểm Tra
https://baikiemtra.com/uploads/bai-kiem-tra-logo.png
Thứ tư - 17/07/2019 22:30
Giải bài tập Toán 9, chương I: bài 3: Liên hệ giữa phép nhân và phép khai phương
Bài 1. Áp dụng quy tắc khai phương một tích, hãy tính:
a) 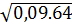 b)
b) 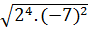 c)
c) 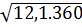 d)
d) 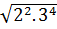 Giải:
a)
Giải:
a)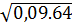 =
= 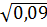 .
. 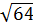 = 0,3.8 = 2,4;
b)
= 0,3.8 = 2,4;
b) 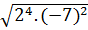 =
= 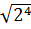 .
. 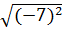 = 22. |-7| = 28;
c)
= 22. |-7| = 28;
c) 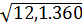 =
=  = 11.6 = 66;
d)
= 11.6 = 66;
d) 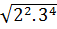 =
= 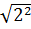 .
. 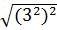 = 2.9 = 18
Bài 2. Áp dụng quy tắc nhân các căn bậc hai, hãy tính:
a)
= 2.9 = 18
Bài 2. Áp dụng quy tắc nhân các căn bậc hai, hãy tính:
a) 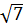 .
. 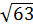 ; b)
; b) 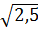 .
. 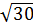 .
. 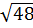 c)
c) 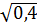 .
. 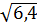 d)
d) 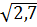 .
. 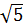 .
. 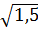 Giải:
a)
Giải:
a) 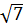 .
. 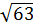 =
= 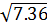 =
= 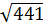 =
= 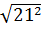 = 21
b)
= 21
b) 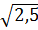 .
.  .
. 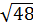 =
= 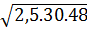 =
= 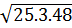 =
= 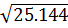 =
= 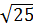 .
. 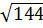 =
= 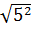 .
. 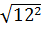 = 5.12 = 60
c)
= 5.12 = 60
c) 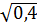 .
. 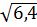 =
= 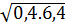 =
= 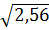 =
= 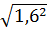 = 1,6
d)
= 1,6
d) 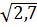 .
. 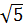 .
. 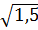 =
= 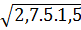 =
= 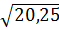 =
= 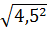 = 4,5
Bài 3. Rút gọn các biểu thức sau:
a)
= 4,5
Bài 3. Rút gọn các biểu thức sau:
a) 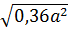 với a < 0 b)
với a < 0 b) 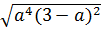 với a
với a 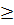 3
c)
3
c) 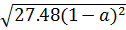 với a > 1 d)
với a > 1 d) 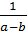 .
. 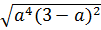 với a > b
Giải:
a)
với a > b
Giải:
a) 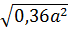 =
= 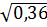 .
. 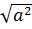 = 0,6.| a | = -0,6a (với a
= 0,6.| a | = -0,6a (với a 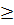 3)
b)
3)
b) 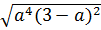 =
= 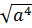 .
. 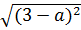 = |
= | 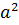 | . | 3 - a| = -a2. (3 - a) (với a
| . | 3 - a| = -a2. (3 - a) (với a 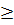 3)
c)
3)
c) 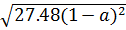 =
= 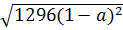 =
= 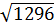 .
. 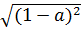 = 36. | 1 - a|2 = -36(1 - a) (Với a > 1)
d)
= 36. | 1 - a|2 = -36(1 - a) (Với a > 1)
d) 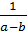 .
. 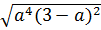 =
= 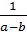
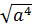 .
. 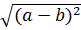 =
= 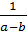 |a|2 . |a – b|
=
|a|2 . |a – b|
= 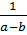 a2. (a - b) = a2 (Với a > b > 0)
Bài 4. Rút gọn các biểu thức sau:
a)
a2. (a - b) = a2 (Với a > b > 0)
Bài 4. Rút gọn các biểu thức sau:
a) 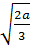 .
. 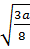 với a
với a 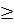 0 ; b)
0 ; b) 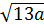 .
. 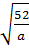 với a > 0;
c)
với a > 0;
c) 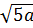 .
. 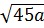 – 3a với a
– 3a với a 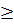 0 d) (3 - a)2 -
0 d) (3 - a)2 - 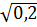 .
. 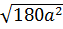 Giải:
a)
Giải:
a) 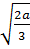 .
. 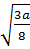 =
= 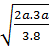 =
= 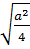 =
= 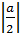 Vì a
Vì a 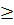 0 ⇒
0 ⇒ 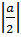 =
=  nên
nên 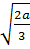 .
. 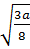 =
=  b) Đáp số: 26
c)
b) Đáp số: 26
c) 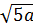 .
. 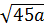 – 3a =
– 3a = 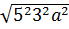 – 3a = 15 | a | - 3a
Với a
– 3a = 15 | a | - 3a
Với a 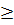 0 ⇒ 15 | a | - 3a = 15a - 3a = 12a
d) (3 - a)2 -
0 ⇒ 15 | a | - 3a = 15a - 3a = 12a
d) (3 - a)2 - 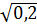 .
. 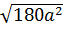 = (3 - a)2 -
= (3 - a)2 - 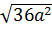 = (3 - a)2 – 6 | a |
* Với a
= (3 - a)2 – 6 | a |
* Với a 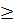 0 ⇒ 6|a| = 6a
(3 - a)2 – 6|a| = 9 – 6a + a2 – 6a = a2 – 12a + 9
* Với a < 0 ⇒ 6 |a| = -6a
(3 - a)2 – 6|a| = 9 – 6a + a2 + 6a = a2 + 9
Bài 5. Khai phương tích 12.30.40 được:
A. 1200 B. 120 C. 12 D. 240
Hãy chọn kết quả đúng.
Giải:
Ta có:
0 ⇒ 6|a| = 6a
(3 - a)2 – 6|a| = 9 – 6a + a2 – 6a = a2 – 12a + 9
* Với a < 0 ⇒ 6 |a| = -6a
(3 - a)2 – 6|a| = 9 – 6a + a2 + 6a = a2 + 9
Bài 5. Khai phương tích 12.30.40 được:
A. 1200 B. 120 C. 12 D. 240
Hãy chọn kết quả đúng.
Giải:
Ta có: 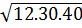 =
= 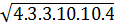 =
= 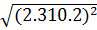 = 2.3.10.2 = 120
Đáp số câu B đúng
BÀI TẬP LÀM THÊM
Bài 1. Thực hiện phép nhân:
a)
= 2.3.10.2 = 120
Đáp số câu B đúng
BÀI TẬP LÀM THÊM
Bài 1. Thực hiện phép nhân:
a) 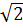 .
. 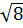 b)
b) 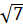 .
. 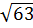 c) 2
c) 2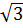 (2
(2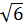 -
- 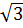 + l)
d) (
+ l)
d) (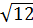 +
+ 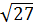 -
- 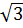 ).
). 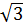 e) (2
e) (2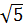 +
+ 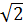 ) (2
) (2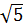 -
- 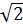 )
Giải:
a)
)
Giải:
a) 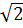 .
. 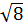 =
= 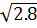 =
= 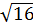 =
= 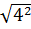 = 4
b)
= 4
b) 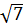 .
. 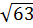 =
= 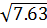 =
= 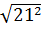 = 21
c) 2
= 21
c) 2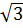 (2
(2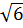 -
- 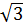 + l) = 4
+ l) = 4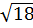 – 6 + 2
– 6 + 2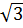 = 4
= 4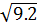 – 6 + 2
– 6 + 2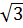 = 12
= 12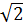 – 6 + 2
– 6 + 2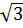 Vậy: 2
Vậy: 2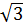 (2
(2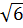 -
- 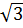 + l) = 12
+ l) = 12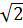 – 6 + 2
– 6 + 2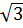 d) (
d) (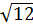 +
+ 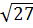 -
- 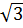 ).
). 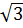 =
= 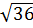 +
+ 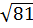 = 6 + 9 - 3 = 12
e) (2
= 6 + 9 - 3 = 12
e) (2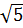 +
+ 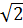 ) (2
) (2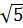 -
- 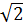 ) = (2
) = (2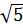 )2 – (
)2 – (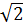 )2 = 20 - 2 = 18
Bài 2. Tìm tất cả các giá trị của x, y, z thỏa mãn đẳng thức:
)2 = 20 - 2 = 18
Bài 2. Tìm tất cả các giá trị của x, y, z thỏa mãn đẳng thức:
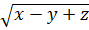 =
= 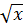 -
- 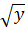 +
+ 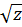 Giải:
Ta có:
Giải:
Ta có: 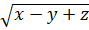 =
= 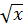 -
- 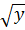 +
+ 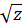 ⇔
⇔ 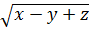 +
+ 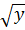 =
= 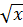 +
+ 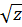 (1)
Điều kiện: x, y, z
(1)
Điều kiện: x, y, z 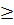 0; x + z
0; x + z 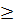 y
Bình phương hai vế của (1) ta được:
x – y + z + y + 2
y
Bình phương hai vế của (1) ta được:
x – y + z + y + 2 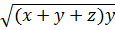 = x + z + 2
= x + z + 2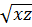 ⇔ y (x – y + z) = xz ⇔ (x - y)(y - z) = 0 ⇔
⇔ y (x – y + z) = xz ⇔ (x - y)(y - z) = 0 ⇔ 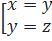 Vậy x, y thỏa mãn yêu cầu đề bài là: x = y
Vậy x, y thỏa mãn yêu cầu đề bài là: x = y 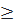 0 hoặc y = z
0 hoặc y = z 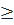 0
Bài 3. Cho a, b
0
Bài 3. Cho a, b 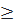 0 chứng minh rằng:
0 chứng minh rằng: 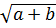
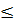
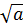 +
+ 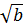 Khi nào xảy ra đẳng thức?
Giải:
Dùng phép biến đổi tương đương, ta có:
Khi nào xảy ra đẳng thức?
Giải:
Dùng phép biến đổi tương đương, ta có:
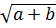
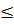
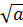 +
+ 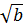 ⇔
⇔ 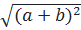
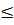 (
(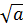 +
+ 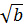 )2
⇔ a + b
)2
⇔ a + b 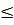 a + 2
a + 2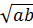 + b ⇔
+ b ⇔ 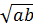
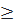 0
Bất đẳng thức cuối cùng luôn đúng nên ta có đpcm. Dấu đẳng thức xảy ra khi và chỉ khi a.b = 0 ⇔ a = 0 hoặc b = 0.
Bài 4. Cho a, b > 0 chứng minh rằng:
0
Bất đẳng thức cuối cùng luôn đúng nên ta có đpcm. Dấu đẳng thức xảy ra khi và chỉ khi a.b = 0 ⇔ a = 0 hoặc b = 0.
Bài 4. Cho a, b > 0 chứng minh rằng: 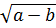
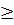
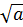 -
- 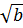 (a
(a 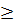 b) Khi nào xảy ra đẳng thức?
Giải:
Ta có:
b) Khi nào xảy ra đẳng thức?
Giải:
Ta có: 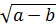
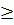
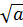 -
- 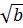 ⇔
⇔ 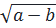 +
+ 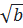
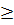
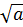 ⇔ (
⇔ (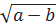 +
+ 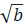 )2
)2  (
(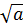 )2
⇔ a – b + 2
)2
⇔ a – b + 2 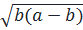 + b
+ b 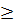 a ⇔ 2
a ⇔ 2 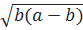
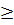 0
Bất đẳng thức cuối cùng đúng nên ta có đpcm. Dấu đẳng thức xảy ra khi b(a - b) = 0
⇔ b = 0 hoặc a = b
Bài 5. Rút gọn biểu thức:
A =
0
Bất đẳng thức cuối cùng đúng nên ta có đpcm. Dấu đẳng thức xảy ra khi b(a - b) = 0
⇔ b = 0 hoặc a = b
Bài 5. Rút gọn biểu thức:
A = 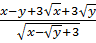 Giải:
Ta có: A =
Giải:
Ta có: A = 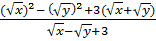 =
= 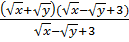 =
= 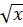 +
+ 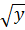 Bài 6. Rút gọn biểu thức:
Q =
Bài 6. Rút gọn biểu thức:
Q = 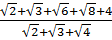 Giải:
Q =
Giải:
Q = 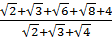 =
= 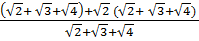 =
= 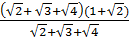 = 1 +
= 1 + 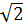
© Bản quyền thuộc về
Bài kiểm tra. Ghi rõ nguồn Bài kiểm tra.com khi sao chép nội dung này.