Giải bài tập Toán 9, chương I: bài 1: Căn bậc hai
2019-07-30T04:34:01-04:00
2019-07-30T04:34:01-04:00
Giải bài tập Toán 9, chương I: bài 1: Căn bậc hai
/themes/cafe/images/no_image.gif
Bài Kiểm Tra
https://baikiemtra.com/uploads/bai-kiem-tra-logo.png
Thứ ba - 16/07/2019 22:24
Giải bài tập Toán 9, chương I: bài 1: Căn bậc hai
Bài 1. Tìm căn bậc hai số học của mỗi số sau rồi suy ra căn bậc hai của chúng: 121; 144; 169; 225; 256; 324; 361; 400
Giải:
Ta có căn bậc hai số học của 121 là 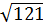 = 11
Vì 11 > 0 và 112 = 121
Tương tự:
= 11
Vì 11 > 0 và 112 = 121
Tương tự: 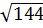 =12;
=12; 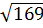 =13;
=13;
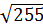 = 15;
= 15; 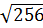 = 16;
= 16;
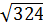 = 18;
= 18; 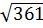 = 19;
= 19; 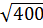 = 20
Bài 2. So sánh:
a) 2 và
= 20
Bài 2. So sánh:
a) 2 và 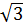 b) 6 và
b) 6 và 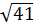 c) 7 và
c) 7 và 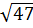 Giải:
a) So sánh 2 và
Giải:
a) So sánh 2 và 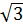 Ta có: 2 =
Ta có: 2 = 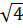 mà 4 > 3 ⇒
mà 4 > 3 ⇒ 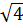 >
> 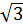 ⇒ 2 >
⇒ 2 > 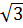 b) So sánh 6 và
b) So sánh 6 và 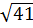 Ta có: 6 =
Ta có: 6 = 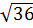 mà 36 < 41 ⇒
mà 36 < 41 ⇒ 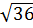 <
< 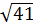 ⇒ 6 <
⇒ 6 < 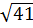 c) So sánh 7 và
c) So sánh 7 và 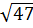 Ta có: 7 =
Ta có: 7 = 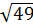 mà 49 > 47 ⇒
mà 49 > 47 ⇒ 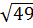 >
> 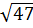 ⇒ 7 >
⇒ 7 > 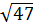 Bài 3. Dùng máy tính bỏ túi để tính nghiệm của các phương trình dưới đây (làm tròn số đến chữ số thập phân thứ ba)
a) x2 = 2; b) x2 = 3; c) x2 = 3,5; d) x2 = 4,12.
Giải:
a) x2 = 2 ⇒ x
Bài 3. Dùng máy tính bỏ túi để tính nghiệm của các phương trình dưới đây (làm tròn số đến chữ số thập phân thứ ba)
a) x2 = 2; b) x2 = 3; c) x2 = 3,5; d) x2 = 4,12.
Giải:
a) x2 = 2 ⇒ x 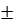
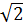 ⇒ x
⇒ x 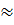 1,4114
b) x2 = 3 ⇒ x
1,4114
b) x2 = 3 ⇒ x 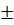
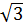 ⇒ x
⇒ x 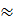 l ,732
c) x2 = 3,5 ⇒ x
l ,732
c) x2 = 3,5 ⇒ x 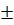
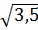 ⇒ x
⇒ x 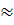 1,871
d) x2 = 4,12 ⇒ x
1,871
d) x2 = 4,12 ⇒ x 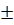
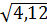 ⇒ x
⇒ x 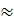
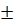 2,030.
Bài 4. Tìm x không âm, biết:
a)
2,030.
Bài 4. Tìm x không âm, biết:
a) 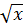 = 15 b) 2
= 15 b) 2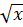 = 14 c)
= 14 c) 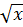 <
< 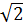 d)
d) 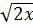 < 4
Giải:
a)
< 4
Giải:
a) 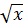 = 15 ⇒ x = 152 ⇒ x = 225;
b) 2
= 15 ⇒ x = 152 ⇒ x = 225;
b) 2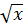 = 14 ⇒ (2
= 14 ⇒ (2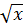 )2 = 142 ⇒ 4x = 196 ⇒ x = 49;
c)
)2 = 142 ⇒ 4x = 196 ⇒ x = 49;
c) 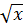 <
< 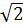 ⇒ (
⇒ ( 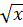 )2 = (
)2 = (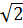 )2 ⇒ x < 4 ⇒ 0 < x < 4;
d)
)2 ⇒ x < 4 ⇒ 0 < x < 4;
d) 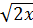 < 4 (
< 4 ( 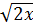 )2 < 42 ⇒ 2x < 16 ⇒ 0 < x < 8
Bài 5. Tính cạnh một hình vuông, biết diện tích của nó bằng diện tích của hình chừ nhật có chiều rộng 3,5m và chiều dài 14m.
)2 < 42 ⇒ 2x < 16 ⇒ 0 < x < 8
Bài 5. Tính cạnh một hình vuông, biết diện tích của nó bằng diện tích của hình chừ nhật có chiều rộng 3,5m và chiều dài 14m.
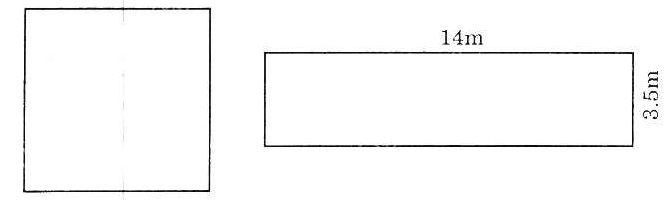 Giải:
Diện tích của hình chữ nhật bằng:
3,5m x 14m = 49 (m2)
Vì diện tích hình chữ nhật bằng diện tích hình vuông nên cạnh hình vuông bằng:
Giải:
Diện tích của hình chữ nhật bằng:
3,5m x 14m = 49 (m2)
Vì diện tích hình chữ nhật bằng diện tích hình vuông nên cạnh hình vuông bằng: 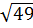 = 7 (m)
Cách khác: Có thể nhẩm theo cách giải hình học là “cắt” đối hình chữ nhật thành hai hình chữ nhật có kích thước 3,5m x 7m và ghép lại được thành hình vuông cạnh 7m.
BÀI TẬP LÀM THÊM
Bài 1. Tính:
a)
= 7 (m)
Cách khác: Có thể nhẩm theo cách giải hình học là “cắt” đối hình chữ nhật thành hai hình chữ nhật có kích thước 3,5m x 7m và ghép lại được thành hình vuông cạnh 7m.
BÀI TẬP LÀM THÊM
Bài 1. Tính:
a) 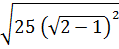 b)
b) 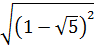 c)
c) 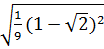 Giải:
a)
Giải:
a) 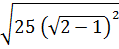 = 5 (
= 5 (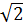 - 1)
b)
- 1)
b) 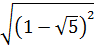 = |1 -
= |1 - 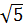 | vì 1 <
| vì 1 < 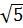 nên |1 -
nên |1 - 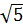 | =
| = 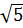 - 1
c)
- 1
c) 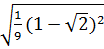 =
=  |1 -
|1 - 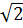 | =
| =  (
(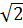 -1) ( vì 1-
-1) ( vì 1- 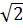 < 0 )
Bài 2. Tính giá trị của các biểu thức sau:
a) 0,5.
< 0 )
Bài 2. Tính giá trị của các biểu thức sau:
a) 0,5. 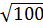 -
- 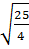 b)
b) 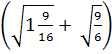 : 5
Giải:
a) 0,5.
: 5
Giải:
a) 0,5. 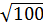 -
- 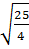 = 0,5
= 0,5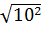 -
- 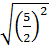 = 0,5.10 -
= 0,5.10 -  = 5 -
= 5 -  =
=  b)
b) 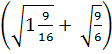 : 5 =
: 5 = 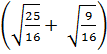 : 5 =
: 5 = 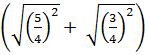 : 5
=
: 5
= 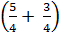 : 5 =
: 5 =  Bài 3: So sánh các số:
a)
Bài 3: So sánh các số:
a) 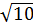 +
+ 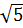 và
và 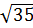 b)
b) 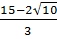 và
và 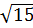 Giải:
Ta có:
a )
Giải:
Ta có:
a ) 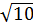 > 3;
> 3; 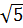 > 2
Nên
> 2
Nên 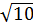 +
+ 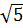 + 1 > 6 và 6 >
+ 1 > 6 và 6 > 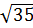 .
.
Vậy 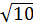 +
+ 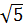 + 1 >
+ 1 > 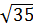 b)
b) 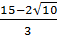 <
< 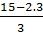 = 3 và
= 3 và 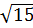 > 3. Vậy
> 3. Vậy 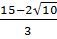 <
< 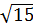 Bài 4. So sánh:
a) 2
Bài 4. So sánh:
a) 2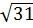 và 10
b) 2 +
và 10
b) 2 + 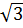 và 3 +
và 3 + 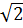 Giải:
a) Áp dụng định lí: a > b
Giải:
a) Áp dụng định lí: a > b 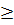 0 ⇔
0 ⇔ 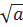 >
> 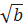 Ta có: 31 > 25 nên
Ta có: 31 > 25 nên 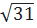 > 5
Hay 2
> 5
Hay 2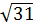 > 10
b) a > b
> 10
b) a > b 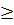 0 ⇔ a2 > b2
Ta có: (2 +
0 ⇔ a2 > b2
Ta có: (2 + 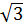 )2 = 7 + 4
)2 = 7 + 4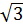 và (3 +
và (3 + 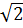 )2 = 11 + 6
)2 = 11 + 6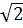 Nhưng: 4
Nhưng: 4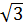 < 6
< 6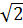 (vì (4
(vì (4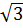 )2 = 48; (6
)2 = 48; (6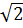 )2 = 72)
Nên: 7+ 4
)2 = 72)
Nên: 7+ 4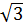 < 11 + 6
< 11 + 6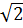 Vậy: 2 +
Vậy: 2 + 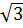 < 3 +
< 3 + 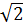 Bài 5. Chứng minh rằng với số thực a, b
Bài 5. Chứng minh rằng với số thực a, b 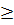 0, ta có:
0, ta có:
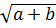
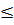
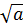 +
+ 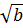 Giải:
Ta có:
Giải:
Ta có: 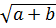
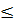
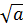 +
+ 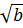 ⇔ (
⇔ (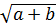 )2
)2 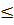 (
(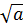 +
+ 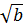 )2 (do
)2 (do 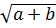
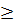 0;
0; 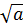 +
+ 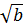
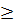 0 )
⇔ a + b
0 )
⇔ a + b 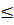 a + b + 2
a + b + 2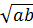 ⇔ 0
⇔ 0 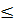 2
2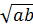 (Bất đẳng thức đúng vì
(Bất đẳng thức đúng vì 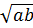
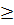 0)
Vậy với mọi số thực a, b
0)
Vậy với mọi số thực a, b 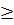 0:
0: 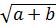
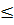
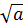 +
+ 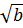 Bài 6. Tìm điều kiện để các biểu thức sau có nghĩa:
a)
Bài 6. Tìm điều kiện để các biểu thức sau có nghĩa:
a) 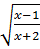 b)
b) 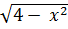 c)
c) 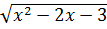 Giải:
Giải:
a)
Ta có:
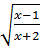 có nghĩa khi
có nghĩa khi 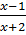
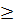 0 ⇔
0 ⇔ 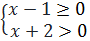 hay
hay 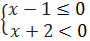 ⇔
⇔ 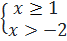 hay
hay 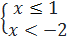 ⇔ x
⇔ x 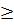 1 hay x < - 2
Vậy với:
1 hay x < - 2
Vậy với: 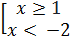 thì
thì 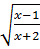 có nghĩa
b)
có nghĩa
b) 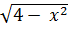 có nghĩa khi 4 – x2
có nghĩa khi 4 – x2 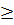 0 ⇔ x2 - 4
0 ⇔ x2 - 4 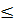 0
⇔ (x - 2)(x+2)
0
⇔ (x - 2)(x+2) 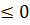 ⇔
⇔ 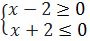 hay
hay 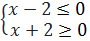 ⇔
⇔ 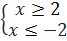 hay
hay 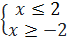 ⇔ -2
⇔ -2 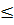 x
x 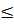 2
Vậy với -2
2
Vậy với -2 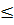 x
x 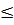 2 thì
2 thì 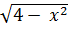 có nghĩa
c)
có nghĩa
c) 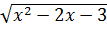 có nghĩa khi x2 - 2x - 3
có nghĩa khi x2 - 2x - 3 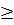 0
⇔ (x+1)(x - 3)
0
⇔ (x+1)(x - 3) 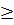 0 ⇔ x
0 ⇔ x 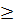 3 hay x
3 hay x 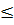 -1
Vậy với :
-1
Vậy với : 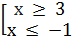 thì
thì 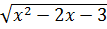 có nghĩa
Bài 7. Chứng minh rằng
có nghĩa
Bài 7. Chứng minh rằng 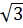 + 1 là số vô tỉ.
Giải:
Giả sử
+ 1 là số vô tỉ.
Giải:
Giả sử 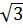 + 1 là số hữu tỉ.
Đặt
+ 1 là số hữu tỉ.
Đặt 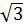 + 1 = x (x
+ 1 = x (x 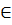 Q), ta có:
(
Q), ta có:
(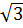 + 1)2 = x2 ⇔ 3 + 2
+ 1)2 = x2 ⇔ 3 + 2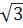 + 1 = x2 ⇔
+ 1 = x2 ⇔ 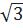 =
= 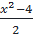 Vì x là số hữu tỉ nên x2 - 4 là số hữu tỉ.
Do đó
Vì x là số hữu tỉ nên x2 - 4 là số hữu tỉ.
Do đó 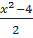 là số hữu tỉ.
Như vậy
là số hữu tỉ.
Như vậy 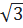 là số hữu tỉ (Điều này vô lí)
Vậy
là số hữu tỉ (Điều này vô lí)
Vậy 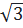 là 1 số vô tỉ.
Bài 8. Chứng minh rằng
là 1 số vô tỉ.
Bài 8. Chứng minh rằng 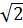 +
+ 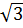 là số vô tỉ
Giải:
Đặt x =
là số vô tỉ
Giải:
Đặt x = 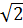 +
+ 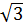 ⇒ (x -
⇒ (x - 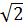 )2 = 3
⇔ x2 - 1 = 2
)2 = 3
⇔ x2 - 1 = 2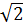 x ⇒ (x2 - 1)2 = 8x2 ⇔ x4 - 10x2 + 1= 0
Như vậy x là nghiệm của phương trình: x4 - 10x2 + 1= 0
Đặt x =
x ⇒ (x2 - 1)2 = 8x2 ⇔ x4 - 10x2 + 1= 0
Như vậy x là nghiệm của phương trình: x4 - 10x2 + 1= 0
Đặt x =  ; giả sử x là số hữu tỉ thì
; giả sử x là số hữu tỉ thì  tối giản.
Ta có:
tối giản.
Ta có: 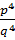 – 10
– 10 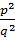 + 1 = 0 ⇔ p4 – 102q2 + q4 = 0 ⇔ p4 = q2(10p2 – q2)
Do đó p4 : q (điều này mâu thuẫn với
+ 1 = 0 ⇔ p4 – 102q2 + q4 = 0 ⇔ p4 = q2(10p2 – q2)
Do đó p4 : q (điều này mâu thuẫn với  tối giản).
Suy ra: x là số vô tỉ.
Bài 9. Tìm giá trị của x để các biểu thức sau được xác định:
a) A =
tối giản).
Suy ra: x là số vô tỉ.
Bài 9. Tìm giá trị của x để các biểu thức sau được xác định:
a) A = 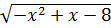 b) B =
b) B = 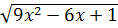 +
+ 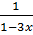 Giải:
a) Biến đổi biểu thức dưới dấu căn, ta được:
Giải:
a) Biến đổi biểu thức dưới dấu căn, ta được:
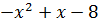 = -
= - 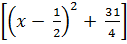 Vì
Vì 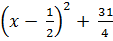 > 0
> 0 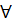 x
x 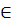 R
nên -
R
nên -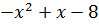 > 0
> 0 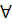 x
x 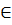 R
Vậy biểu thức đã cho xác định với mọi x.
b) Điều kiện:
R
Vậy biểu thức đã cho xác định với mọi x.
b) Điều kiện: 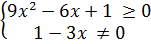 Vậy x
Vậy x 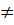

© Bản quyền thuộc về
Bài kiểm tra. Ghi rõ nguồn Bài kiểm tra.com khi sao chép nội dung này.

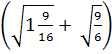 : 5
: 5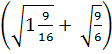 : 5 =
: 5 = 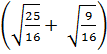 : 5 =
: 5 = 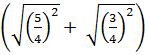 : 5
: 5