Giải bài tập Toán 9, chương II: Bài 1: Nhắc lại và bổ sung các khái niệm về hàm số
2019-07-30T04:33:32-04:00
2019-07-30T04:33:32-04:00
Giải bài tập Toán 9, chương II: Bài 1: Nhắc lại và bổ sung các khái niệm về hàm số
/themes/cafe/images/no_image.gif
Bài Kiểm Tra
https://baikiemtra.com/uploads/bai-kiem-tra-logo.png
Thứ ba - 30/07/2019 04:28
Giải bài tập Toán 9, chương II: Bài 1: Nhắc lại và bổ sung các khái niệm về hàm số
Bài 1. a) Cho hàm số y = f(x) =  x.
Tính: f(-2); f(-1); f(0); f
x.
Tính: f(-2); f(-1); f(0); f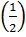 ; f(1); f(2); f(3)
b) Cho hàm số y = g(x) =
; f(1); f(2); f(3)
b) Cho hàm số y = g(x) =  x + 3.
Tính: g(-2); g(-1); g(0); g
x + 3.
Tính: g(-2); g(-1); g(0); g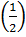 ; g(1); g(2); g(3)
c) Có nhận xét gì về giá trị của hai hàm số đã cho ở trên khi biến x lấy cùng một giá trị?
Giải:
a) y = f(x) =
; g(1); g(2); g(3)
c) Có nhận xét gì về giá trị của hai hàm số đã cho ở trên khi biến x lấy cùng một giá trị?
Giải:
a) y = f(x) =  x.
* f(-2) =
x.
* f(-2) =  . (-2) = -
. (-2) = -  * f(1) =
* f(1) =  * f(-1) = -
* f(-1) = -  * f(2) =
* f(2) =  * f(0) = 0 * f(3) = 2
* f
* f(0) = 0 * f(3) = 2
* f 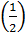 =
=  b) y = g(x) =
b) y = g(x) =  x + 3
* g(-2) =
x + 3
* g(-2) =  * g
* g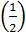 =
= 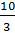 * f(2) =
* f(2) = 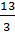 * g(-1) =
* g(-1) =  * g(1) =
* g(1) =  * g(3) = 5
* g (0) = 3
c) Nhận xét:
Giá trị của hàm số y = g(x) =
* g(3) = 5
* g (0) = 3
c) Nhận xét:
Giá trị của hàm số y = g(x) =  x + 3 lớn hơn giá trị của hàm số y = f(x) =
x + 3 lớn hơn giá trị của hàm số y = f(x) =  x là 3 đơn vị khi biến x lấy cùng một giá trị.
Bài 2. Cho hàm số y = -
x là 3 đơn vị khi biến x lấy cùng một giá trị.
Bài 2. Cho hàm số y = -  x + 3.
a) Tính các giá trị tương ứng của y theo các giá trị của x rồi điền vào bảng sau:
x + 3.
a) Tính các giá trị tương ứng của y theo các giá trị của x rồi điền vào bảng sau:
| x |
-2,5 |
-2 |
-1,5 |
-1 |
- 0,5 |
0 |
0,5 |
1 |
1,5 |
2 |
2,5 |
y = -  x + 3 x + 3 |
|
|
|
|
|
|
|
|
|
|
|
b) Hàm số đã cho là hàm số đồng biến hay nghịch biến? Vì sao?
Giải:
a) Với y = -  x + 3, ta có:
* f(-2,5) = -
x + 3, ta có:
* f(-2,5) = -  (-2,5) + 3 = 2
(-2,5) + 3 = 2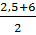 =
= 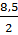 = 4,25
* f(-2) = -
= 4,25
* f(-2) = -  . (-2) + 3 = 4
* f(-1,5) = -
. (-2) + 3 = 4
* f(-1,5) = -  . (-1,5) + 3=
. (-1,5) + 3= 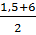 =
= 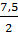 = 3,75
* f(-1) = -
= 3,75
* f(-1) = -  (-1) + 3=
(-1) + 3= 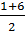 =
=  = 3,5
* f(-0,5) = -
= 3,5
* f(-0,5) = -  (-0,5) + 3=
(-0,5) + 3= 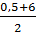 =
= 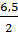 = 3,25
* f(0) = -
= 3,25
* f(0) = -  .0 + 3 = 3
* f(0,5) = -
.0 + 3 = 3
* f(0,5) = -  . 0,5 + 3=
. 0,5 + 3= 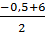 =
= 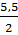 = 2,75
* f( 1) = -
= 2,75
* f( 1) = -  . 1 + 3=
. 1 + 3= 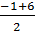 =
=  = 3,5
* f(1,5) = -
= 3,5
* f(1,5) = -  . 1,5 + 3=
. 1,5 + 3= 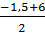 =
= 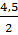 = 2,25
* f(2) = -
= 2,25
* f(2) = -  . 2 + 3= 2
* f(2,5) = -
. 2 + 3= 2
* f(2,5) = -  . 1,5 + 2,5=
. 1,5 + 2,5= 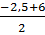 =
= 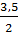 = 1,75
Điền vào bảng ta được:
= 1,75
Điền vào bảng ta được:
| x |
-2,5 |
-2 |
-1,5 |
-1 |
- 0,5 |
0 |
0,5 |
1 |
1,5 |
2 |
2,5 |
y = -  x + 3 x + 3 |
4,25 |
4 |
3,75 |
3,5 |
3,25 |
3 |
2,75 |
2,5 |
2,25 |
2 |
1,75 |
b) Hàm số y = -  x + 3 là hàm số nghịch biến vì khi giá trị của biến x càng tăng thì giá trị tương đương của hàm y lại giảm đi.
Bài 3. Cho hai hàm số y = 2x và y = -2x.
a) Vẽ trên cùng một mặt phẳng tọa độ đồ thị cua hai hàm số đã cho.
b) Trong hai hàm số đã cho hàm số nào đồng biến? Hàm số nào nghịch biến? Vì sao?
Giải:
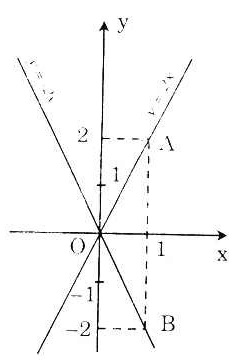
a) Để vẽ đồ thị hàm số y = 2x ta lấy điểm A(1; 2).
Đường thẳng OA là đồ thị của hàm số y = 2x.
Lấy điểm B(1; -2). Đường thẳng OB là đồ thị hàm số y = -2x.
x + 3 là hàm số nghịch biến vì khi giá trị của biến x càng tăng thì giá trị tương đương của hàm y lại giảm đi.
Bài 3. Cho hai hàm số y = 2x và y = -2x.
a) Vẽ trên cùng một mặt phẳng tọa độ đồ thị cua hai hàm số đã cho.
b) Trong hai hàm số đã cho hàm số nào đồng biến? Hàm số nào nghịch biến? Vì sao?
Giải:
a) Để vẽ đồ thị hàm số y = 2x ta lấy điểm A(1; 2).
Đường thẳng OA là đồ thị của hàm số y = 2x.
Lấy điểm B(1; -2). Đường thẳng OB là đồ thị hàm số y = -2x.
b) Trong hai hàm số y = 2x và y = -2x thì hàm số y = 2x là hàm số đồng biến, vì rõ ràng là ứng với giá trị lớn hơn của biến số x thì ta được giá trị y lớn hơn.
Hàm số y = -2x là hàm số nghịch biến vì ứng với giá trị lớn hơn của x thì ta được giá trị của y nhỏ hơn. |
 |
Ta xét bảng sau:
| y = 2x |
-1 |
0 |
1 |
2 |
| y = -2x |
-2 |
0 |
2 |
4 |
| y = -2x |
2 |
0 |
-2 |
-4 |
BÀI TẬP LÀM THÊM
Bài 1. Tìm hàm số f(x) biết:
2f(x) + f(1 - x) = 2x + 3 với mọi x.
Giải:
Đặt y = 1 - x ⇒ x = 1 - y Theo đề bài ta có:
2f(1 - y) + f(y) = 2(1 - y) + 3 = 5 - 2y
⇒ 2f(1 - x) + f(x) = 5 – 2x (1)
Mà: f(1 - x) + 2f(x) = 2x + 3
⇒ 2f(1 - x) + 4f(x) = 4x + 6 (2)
Lấy (2) – (1) ta được: 3f(x) = 6x + 1
Vậy: f(x) = 2x +  Bài 2. Chứng minh rằng:
a) Hàm số y = 2x luôn luôn đồng biến trên tập R
b) Hàm số y = -2x luôn luôn nghịch biến trên tập R
c) Hàm số y = ax luôn luôn đồng biến trên tập R nếu a > 0 và nghịch biến trên R nếu a < 0
Giải:
Hàm số y = 2x xác định R
Với x1, x2
Bài 2. Chứng minh rằng:
a) Hàm số y = 2x luôn luôn đồng biến trên tập R
b) Hàm số y = -2x luôn luôn nghịch biến trên tập R
c) Hàm số y = ax luôn luôn đồng biến trên tập R nếu a > 0 và nghịch biến trên R nếu a < 0
Giải:
Hàm số y = 2x xác định R
Với x1, x2 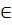 và x1
và x1 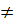 x2 : ta có: y1= 2x1; y2 = 2x2
⇒ y2 – y1= 2x2 – 2x1 = 2(x2 – x1) ⇔
x2 : ta có: y1= 2x1; y2 = 2x2
⇒ y2 – y1= 2x2 – 2x1 = 2(x2 – x1) ⇔ 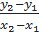 = 2 > 0
Do đó hàm số y = 2x luôn luôn đồng biến trên tập R
b) Hàm số y = -2x xác định
= 2 > 0
Do đó hàm số y = 2x luôn luôn đồng biến trên tập R
b) Hàm số y = -2x xác định 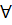 x
x 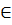 R
Tương tự ta có: ⇔
R
Tương tự ta có: ⇔ 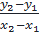 = -2 < 0
Do đó hàm số y = -2x luôn luôn nghịch biến trên tập R
c) Hàm số y = ax xác định
= -2 < 0
Do đó hàm số y = -2x luôn luôn nghịch biến trên tập R
c) Hàm số y = ax xác định 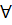 x
x 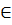 R
Với x1, x2
R
Với x1, x2 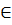 R và x1
R và x1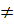 x2, ta có: y1 = ax1; y2 = ax2
⇒ y2 – y1 = ax2 – ax1 = a(x2 – x1) ⇔
x2, ta có: y1 = ax1; y2 = ax2
⇒ y2 – y1 = ax2 – ax1 = a(x2 – x1) ⇔ 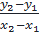 = a > 0
+ Nếu a > 0 ⇒
= a > 0
+ Nếu a > 0 ⇒ 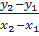 > 0 hàm đồng biến.
+ Nếu a < 0 ⇒
> 0 hàm đồng biến.
+ Nếu a < 0 ⇒ 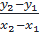 < 0 hàm nghịch biến.
Bài 3. Cho a, b
< 0 hàm nghịch biến.
Bài 3. Cho a, b 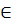 R với a
R với a 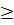 0, Chứng minh rằng tồn tại hàm số y = f(x) với x
0, Chứng minh rằng tồn tại hàm số y = f(x) với x 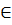 R sao cho f[f(x)] = ax + b với mọi x
R sao cho f[f(x)] = ax + b với mọi x 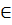 R
Giải:
Chọn f(x) =
R
Giải:
Chọn f(x) = 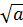 .x +
.x + 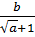 x
x 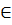 R
f[f(x)] =
R
f[f(x)] = 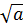 . f(x) +
. f(x) + 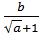 =
= 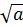
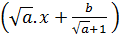 +
+  = ax +
= ax + 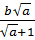 +
+ 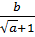 = ax +
= ax + 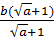 = ax + b
= ax + b
© Bản quyền thuộc về
Bài kiểm tra. Ghi rõ nguồn Bài kiểm tra.com khi sao chép nội dung này.
