Giải bài tập Toán 9, chương II: Bài 3: Đồ thị hàm số y = ax + b (a ≠ 0)
2019-07-31T04:34:31-04:00
2019-07-31T04:34:31-04:00
Giải bài tập Toán 9, chương II: Bài 3: Đồ thị hàm số y = ax + b (a ≠ 0)
/themes/cafe/images/no_image.gif
Bài Kiểm Tra
https://baikiemtra.com/uploads/bai-kiem-tra-logo.png
Thứ tư - 31/07/2019 04:30
Giải bài tập Toán 9, chương II: Bài 3: Đồ thị hàm số y = ax + b (a ≠ 0)
Bài 1. a) Vẽ đồ thị của các hàm số: y = 2x; y = 2x + 5; y = -  x và y = -
x và y = -  x + 5 trên cùng một hệ trục tọa độ.
b) Bốn đường thẳng trên cắt nhau tạo thành tứ giác OABC (O là gốc tọa độ). Tứ giác OABC có phải là hình chữ nhật không? Vì sao?
Giải:
x + 5 trên cùng một hệ trục tọa độ.
b) Bốn đường thẳng trên cắt nhau tạo thành tứ giác OABC (O là gốc tọa độ). Tứ giác OABC có phải là hình chữ nhật không? Vì sao?
Giải:
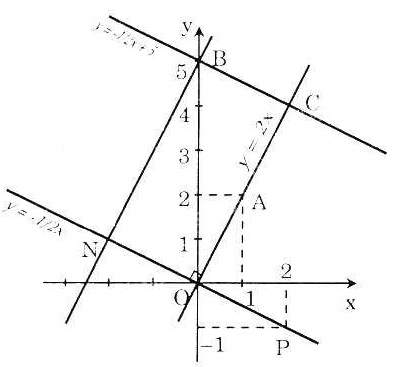
a) Vẽ đồ thị các hàm số: y = 2x.
Đồ thị hàm số y = 2x là một dường thẳng đi qua gốc tọa độ 0(0; 0) và điểm A(1; 2)
* y = 2x + 5
- Cho x = 0; tính được y = 5. Ta xác định điểm B(0; 5)
- Cho y = 0, tính được x = - 
Ta xác định điểm N (-  ; 0) ; 0)
Đồ thị hàm số y = 2x + 5 là đường thẳng đi qua 2 điểm N và B.
y = -  x x
Đồ thị hàm số y = -  x là một đường thẳng đi qua gốc tọa độ 0(0; 0) và đi qua điểm P(2; -1). x là một đường thẳng đi qua gốc tọa độ 0(0; 0) và đi qua điểm P(2; -1).
y = -  x + 5 x + 5
- Cho x = 0, tính được y = 5. Ta xác định được điểm B(0; 5 ).
- Cho x = 2, ta tính được y = 4. Ta xác định được điểm C(2; 4).
Đồ thị hàm số -  x + 5 là một đường thẳng đi qua hai điểm B và C. x + 5 là một đường thẳng đi qua hai điểm B và C.
b) Bốn đường thẳng đã cho ở trên cắt nhau tại các điểm O, A, B, C.
- Vì đường thẳng y = 2x song song với đường thẳng y = 2x + 5 và đường thẳng y = -  x . Song song với đường thẳng y = - x . Song song với đường thẳng y = -  x + 5. x + 5.
Do đó, tứ giác OABC là hình bình hành (vì chung có 2 cặp cạnh đối song song).
- Hai đường thẳng y = 2x và y = -  x có tích các hệ số góc là: x có tích các hệ số góc là:
a.a’ = 2(-  ) = -1 ) = -1
Vậy hai đường thẳng đó vuông góc với nhau.
Vậy tứ giác OABC là hình chữ nhật. |
 |
Bài 2. a) Vẽ đồ thị của các hàm số y = x và y = 2x + 2 trên cùng một mặt phẳng tọa độ.
b) Gọi A là giao điểm của hai đồ thị nói trên, tìm tọa độ điểm A.
c) Vẽ qua điểm B(0; 2) một đường thẳng song song với trục Ox, cắt đường thẳng y = x tại điểm C. Tìm tọa độ của điểm C rồi tính diện tích tam giác ABC (đơn vị đo trên các trục tọa độ là xentimét).
Giải:
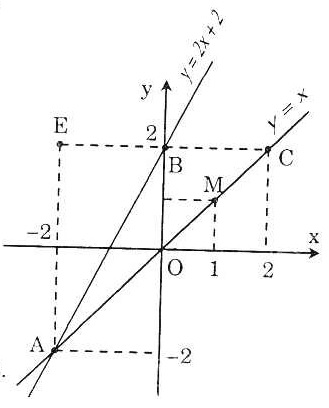
a) * Đồ thị hàm số y = x là đường thẳng đi qua hai điểm O và M(1;1).
* Đồ thị hàm số y = 2x + 2 là đường thẳng đi qua hai điểm B(0; 2) và D (-1; 0)
b) A là giao điểm của hai đường thẳng y = x và y = 2x + 2 nên hoành độ điểm A là nghiệm của phương trình:
x = 2x + 2 ⇔ x = - 2.
Với x = - 2 thì y = - 2 (thế vào đường thẳng y = x).
Vậy A(-2; -2).
c) Đường thẳng qua B(0; 2) và song song với Ox có phương trình: y = 2
Hoành độ điểm C là nghiệm của phương trình: 2 = x.
Vậy C(2; 2).
Qua A kẻ đường thẳng song song với Oy cắt đường thắng BC tại E
Dễ thấy AE ⊥ BC và BC = 2; AE = 4.
Do đó: 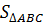 = =  BC.AE = BC.AE =  .2.4 = 4 .2.4 = 4
Vậy: 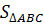 = 4cm2. = 4cm2. |
 |
BÀI TẬP LÀM THÊM
Bài 1. Cho hàm số: y = (a - 1)x + 2
a) Xác định a để đồ thị hàm số cắt trục hoành tại điểm có hoành độ bằng -1.
b) Vẽ đồ thị hàm số vừa tìm được.
Giải:
a) Đồ thị hàm số đi qua điểm B(-1; 0) nên:
0 = (a -1)(-1) + 2
⇒ a = 3
Vậy y = 2x + 2
b) Vẽ đồ thị Đồ thị hàm số y = 2x + 2 đi qua hai điểm A(0; 2) và B(-1; 0). |
 |
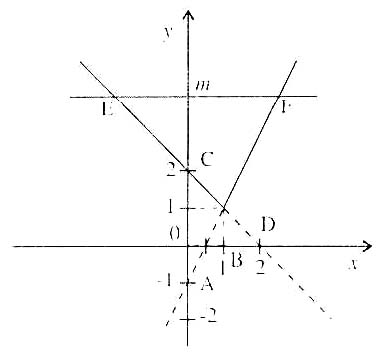
Bài 2. Vẽ đồ thị hàm số:
y = 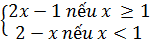 Với giá trị nào của m thì đường thẳng y = m cắt đồ thị hàm số tại hai điểm phân biệt? Tìm giao điểm của hai đồ thị trên.
Giải:
Với giá trị nào của m thì đường thẳng y = m cắt đồ thị hàm số tại hai điểm phân biệt? Tìm giao điểm của hai đồ thị trên.
Giải:
Đồ thị hàm số y = 2x - 1 qua 2 điểm A(0; -1), B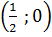
Đồ thị hàm số y = 2 - x qua 2 điểm C(0; 2), D(2; 0). Đồ thị hàm số đã cho là:
Đường thẳng y = m là đường thẳng song song với trục hoành tại điểm M(0; m). Khi m thay đổi thì đường thẳng y = m sẽ di chuyển lên xuống song song với trục hoành.
Nhìn đồ thị ta thấy với m > 1 thì đường thẳng y = m cắt đồ thị hàm số đã cho tại hai điểm phân biệt E và F.
Giao điểm E là giao điểm của hai đường thẳng y = m và y = 2 - x.
Với y = m thì 2 - x = m ⇒ x = 2 - m.
Vậy E(2 - m; m).
Tương tự F 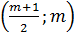 |
 |
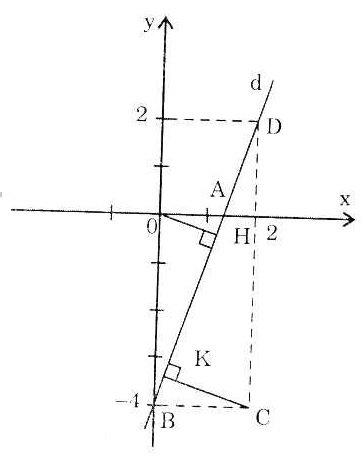
Bài 3. Vẽ đường thẳng (d): y = 3x - 4
a) Xác định giao điểm A, B của (d) với Ox và Oy. Suy ra khoảng cách từ O đến (d).
b) Tính khoáng cách từ điểm C(2; - 4) tới (d).
Giải:
a) x = 0; y = - 4 và x = 2; y = 2. Đường thẳng (d) là đường thẳng qua hai điểm (0; -4) và (2; 2)
Cho y = 0; x =  ⇒ A ⇒ A 
Cho x = 0; y = - 4 ⇒ B (0; - 4)
Kẻ OH vuông góc với (d).
Trong tam giác OAB, ta có:
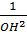 = = 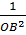 + + 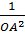
= 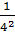 + + 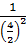 = = 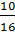
Vậy khoảng cách từ O tới (d) là OH = 
b) Qua C vẽ đường thẳng song song trục hoành cắt (d) tại B(0; - 4), và đường thẳng song song trục tung cắt (d) tại D(2; 2). Từ C kẻ CK vuông góc với d tại K. Trong tam giác CBD, ta có:
CB = 2 và CD = 2 + 4 = 6
Và: 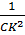 = = 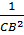 + + 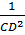 = =  + +  = = 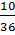 ⇒ CK = ⇒ CK = 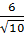
Vậy khoảng cách cần tìm là: 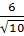 |
 |
Bài 4. Cho các đường thẳng:
(d1): y = x + 2; (d2): y = -2x + 5
(d3): y = 3x; (d4): y - mx + m - 5
Trong cùng một hệ trục tọa độ:
a) Chứng minh: (d1), (d2), (d3) đồng quy.
b) Tìm m để (d1), (d2), (d3) và (d4) đồng quy.
Giải:
a) Gọi A là giao điểm (nêu có) của (d1) và (d3). Ta có:
x + 2 = 3x ⇔ 2x = 2 ⇔ x = 1
x = 1 thì y = 1 + 2 = 3
Vậy (d1) cắt (d3) tại A(1; 3)
A(1; 3) 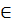 (d2) ⇔ 3 = -2.1 + 5 ⇔ 3 = 3 (đúng)
Ta có: A
(d2) ⇔ 3 = -2.1 + 5 ⇔ 3 = 3 (đúng)
Ta có: A 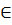 (d2)
Do đó (d1), (d2), (d3) đồng quy.
b) (d1), (d2), (d3) đồng quy tại A.
Ta có: (d1), (d2), (d3) và (d) đồng quy
⇔ A
(d2)
Do đó (d1), (d2), (d3) đồng quy.
b) (d1), (d2), (d3) đồng quy tại A.
Ta có: (d1), (d2), (d3) và (d) đồng quy
⇔ A 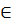 (d) ⇔ 3 - m.1 + m - 5 ⇔ 2m = 8 ⇔ m = 4
Bài 5. a) Vẽ đồ thị hàm số y = x
(d) ⇔ 3 - m.1 + m - 5 ⇔ 2m = 8 ⇔ m = 4
Bài 5. a) Vẽ đồ thị hàm số y = x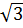 b) Tìm tung độ các điểm A, B, c nằm trên đồ thị có hoành độ -2,
c) Gọi
b) Tìm tung độ các điểm A, B, c nằm trên đồ thị có hoành độ -2,
c) Gọi 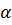 là góc hợp bởi tia Ox và đường thắng y = x
là góc hợp bởi tia Ox và đường thắng y = x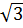 . Tính
. Tính 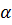 .
Giải:
.
Giải:
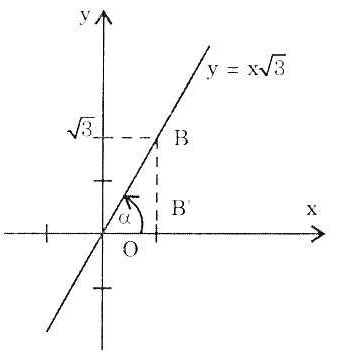
a) Đồ thị hàm số y = x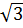 là đường thẳng đi qua gốc O và điểm B(1; là đường thẳng đi qua gốc O và điểm B(1; 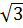 ), từ trái lên phải. ), từ trái lên phải.
b) Điểm A có hoành độ x = -2 nên có tung độ là: y = - 2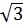
Điểm B có hoành độ x = 1 nên có tung độ là: y = 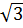
Điểm C có hoành độ x = 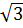 nên có tung độ là: y = nên có tung độ là: y = 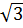 . .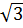 = 3 = 3
c) Trong tam giác vuông OB’B, ta có:
tg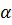 = ' = '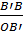 = = 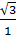 = = 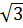 ⇒ ⇒ 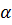 = 60o = 60o |
 |
Bài 6. Cho hai hàm sô y = 2x và y = -3x + 5.
a) Vẽ trên cùng một hệ trục tọa độ đồ thị của hai hàm số trên.
b) Gọi M là giao điểm của hai đồ thị; A và B theo thứ tự là giao điểm của đường thẳng y = -3x + 5 với trục hoành và trục tung. Tính độ dài các đoạn thẳng AB và diện tích các tam giác AOB và AOM.
Giải:
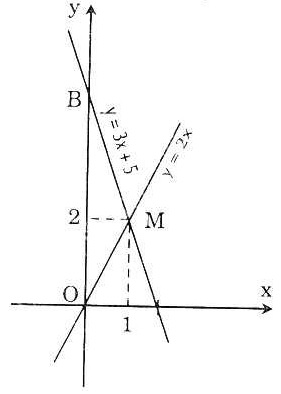
a) Đồ thị hàm số y = 2x và y = 3x + 5 (Xem hình vẽ)
b) Giao điểm của hai đồ thị là điểm M(1; 2). Đường thẳng y = 3x + 5 cắt trục hoành tại điểm A 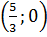 và điểm B (0; 5). và điểm B (0; 5).
Tam giác vuông AOB ta có:
AB2 = OA2 + OB2
= 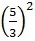 + 52 = + 52 = 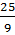 + 25 = + 25 = 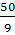
⇒ AB = 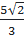 (đơn vị độ dài) (đơn vị độ dài)
SAOB =  = = 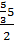 = = 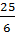 = 4 = 4 (đơn vị diện tích) (đơn vị diện tích)
SAOM =  . .  .2 = .2 =  = 1 = 1 (đơn vị diện tích) (đơn vị diện tích) |
 |
© Bản quyền thuộc về
Bài kiểm tra. Ghi rõ nguồn Bài kiểm tra.com khi sao chép nội dung này.






