Giải bài tập Toán 9, chương II: Bài 2: Hàm số bậc nhất
2019-07-30T23:24:02-04:00
2019-07-30T23:24:02-04:00
Giải bài tập Toán 9, chương II: Bài 2: Hàm số bậc nhất
/themes/cafe/images/no_image.gif
Bài Kiểm Tra
https://baikiemtra.com/uploads/bai-kiem-tra-logo.png
Thứ ba - 30/07/2019 23:04
Giải bài tập Toán 9, chương II: Bài 2: Hàm số bậc nhất
Bài 1. Trong các hàm số sau, hàm số náo là hàm sô bậc nhất? Hãy xác định hệ số a, b của chúng và xét xem hàm số bậc nhất nào đồng biến, nghịch biến,
a) y = 1 - 5x; b) y = - 0,5x;
c) y = 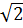 (x - 1) +
(x - 1) + 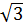 ; d) y = 2x2 + 3.
Giải:
a) Hàm số y = 1 - 5x là hàm số bậc nhất, với a = -5 và b = 1.
+ Vì a = -5 < 0 nên hàm số nghịch biến.
b) Hàm số y = -0,5 là hàm số bậc nhất, với a = - 0,5 và b = 0.
+ Vì a = - 0,5 < 0 nên hàm số nghịch biến.
c) Hàm số y =
; d) y = 2x2 + 3.
Giải:
a) Hàm số y = 1 - 5x là hàm số bậc nhất, với a = -5 và b = 1.
+ Vì a = -5 < 0 nên hàm số nghịch biến.
b) Hàm số y = -0,5 là hàm số bậc nhất, với a = - 0,5 và b = 0.
+ Vì a = - 0,5 < 0 nên hàm số nghịch biến.
c) Hàm số y = 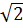 (x - 1) +
(x - 1) + 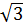 có thể viết lại: y =
có thể viết lại: y = 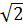 x +
x + 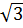 -
- 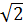 Đây là hàm số bậc nhất với a =
Đây là hàm số bậc nhất với a = 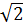 và b =
và b = 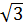 -
- 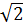 .
+ Vì a =
.
+ Vì a = 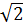 > 0 nên hàm số đồng biến.
d) Hàm số y = 2x2 + 3 không là hàm số bậc nhất vì không có dạng: y = ax + b.
Bài 2. Cho hàm số bậc nhất y = (m - 2)x + 3
a) Tìm các giá trị của m để hàm số đồng biến.
b) Tìm các giá trị của m để hàm số nghịch biến.
Giải:
a) Để hàm số y = (m - 2)x + 3 đồng biến thì m - 2 > 0 ⇒ m > 2
b) Đáp số: m < 2.
Chú ý: Khi m = 2. ta có hàm hằng y = 3.
Bài 3. Một hình chữ nhật có kích thước là 20cm và 30cm. Người ta bớt mỗi kích thước của hình đó đi x (cm) được hình chữ nhật mới chu vi là y (cm). Hãy lập công thức tính y theo x.
Giải:
> 0 nên hàm số đồng biến.
d) Hàm số y = 2x2 + 3 không là hàm số bậc nhất vì không có dạng: y = ax + b.
Bài 2. Cho hàm số bậc nhất y = (m - 2)x + 3
a) Tìm các giá trị của m để hàm số đồng biến.
b) Tìm các giá trị của m để hàm số nghịch biến.
Giải:
a) Để hàm số y = (m - 2)x + 3 đồng biến thì m - 2 > 0 ⇒ m > 2
b) Đáp số: m < 2.
Chú ý: Khi m = 2. ta có hàm hằng y = 3.
Bài 3. Một hình chữ nhật có kích thước là 20cm và 30cm. Người ta bớt mỗi kích thước của hình đó đi x (cm) được hình chữ nhật mới chu vi là y (cm). Hãy lập công thức tính y theo x.
Giải:
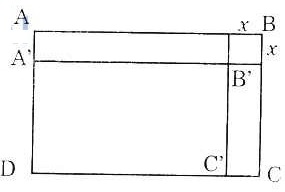
Gọi hình chữ nhật ban đầu ABCD , có kích thước là AB = 30cm; BC = 20cm.
- Sau khi bớt các kích thước của hình chữ nhật x(cm ), ta có hình chữ nhật mới A’B’C’D’ với kích thước là:
A’B’ = 30 - x, BC = 20 - x.
- Gọi y là chu vi của hình chữ nhật A’B’C’D’ ta có:
y = 2[(30 - x) + (20 - x)] = 2(50 - 2x) hay y = - 4x + 100 |
 |
Vì chu vi y phụ thuộc vào đại lượng thay đổi x (x nhận giá trị thay đổi từ 0 đến 20) và với mỗi giá trị xác định của x luôn xác định được một giá trị y duy nhất.
Vậy y là hàm số của x và là hàm số bậc nhất với biến số x
(Vì y có dạng y = ax + b với a 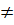 0)
BÀI TẬP LÀM THÊM
Bài 1. Cho hàm số y = f(x) = ax.
Chứng minh rằng: f(k.x) = kf(x)
f(x1 + x2) = f(x1) + f(x2)
Các hệ thức trên có còn đúng với y = f(x) = ax + b, với b
0)
BÀI TẬP LÀM THÊM
Bài 1. Cho hàm số y = f(x) = ax.
Chứng minh rằng: f(k.x) = kf(x)
f(x1 + x2) = f(x1) + f(x2)
Các hệ thức trên có còn đúng với y = f(x) = ax + b, với b 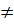 0 không?
Giải:
Ta có: f(k.x) = a(k.x) = k(ax) = k.f(x)
f (x1 + x2) = a(x1 + x2) = ax1 + ax2 = f(x1) + f(x2)
Với f(x) = ax + b (b
0 không?
Giải:
Ta có: f(k.x) = a(k.x) = k(ax) = k.f(x)
f (x1 + x2) = a(x1 + x2) = ax1 + ax2 = f(x1) + f(x2)
Với f(x) = ax + b (b 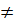 0), với k
0), với k 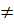 1:
f(k.x) = a(k.x) + b
1:
f(k.x) = a(k.x) + b 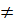 k (ax + b) = k.f(x) (vì b
k (ax + b) = k.f(x) (vì b 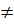 0)
f(x1 + x2) = a(x1 + x2) + b = (ax1 + b) + (ax2 + b) = f (x1) + f (x2)
Bài 2. a) Tìm hàm số bậc nhất biết hệ số góc bằng -1 và đồ thị hàm số đi qua điểm A(2, 3).
b) Tìm hàm số bậc nhất biết đồ thị của nó qua 2 điểm A(-1, 2); B(2, -1).
Giải:
a) Ta có: a = -1 nên y = -x + b (1)
Đồ thị qua A(2, 3) nên thay x = 2, y = 3 vào (1) thì được:
3 = -2 + b ⇒ b = 5
Vậy y = - x + 5
b) Giả sử y = ax + b
Đồ thị qua A(-1, 2) nên: 2 = -a + b qua B(2, -1) nên: -1 = 2a + b
Suy ra :
0)
f(x1 + x2) = a(x1 + x2) + b = (ax1 + b) + (ax2 + b) = f (x1) + f (x2)
Bài 2. a) Tìm hàm số bậc nhất biết hệ số góc bằng -1 và đồ thị hàm số đi qua điểm A(2, 3).
b) Tìm hàm số bậc nhất biết đồ thị của nó qua 2 điểm A(-1, 2); B(2, -1).
Giải:
a) Ta có: a = -1 nên y = -x + b (1)
Đồ thị qua A(2, 3) nên thay x = 2, y = 3 vào (1) thì được:
3 = -2 + b ⇒ b = 5
Vậy y = - x + 5
b) Giả sử y = ax + b
Đồ thị qua A(-1, 2) nên: 2 = -a + b qua B(2, -1) nên: -1 = 2a + b
Suy ra : 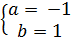 Vậy y = -x + 1
Bài 3. Tìm giá trị của m để hàm số: y = (m2 - 6m + 5)x
a) Đồng biến. b) Nghịch biến.
Giải:
a) Hàm số y = (m2 - 6m + 5)x đồng biến khi hệ số a dương, nghĩa là m2 - 6m + 5 > 0
Hay m2 - 5m + 5 > 0 ⇔ m (m - 1) - 5(m - 1) > 0
⇔ (m -1)(m - 5) > 0 ⇔
Vậy y = -x + 1
Bài 3. Tìm giá trị của m để hàm số: y = (m2 - 6m + 5)x
a) Đồng biến. b) Nghịch biến.
Giải:
a) Hàm số y = (m2 - 6m + 5)x đồng biến khi hệ số a dương, nghĩa là m2 - 6m + 5 > 0
Hay m2 - 5m + 5 > 0 ⇔ m (m - 1) - 5(m - 1) > 0
⇔ (m -1)(m - 5) > 0 ⇔ 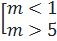 Vậy hàm số đồng biến khi m < 1 hoặc m > 5
b) Hàm số y = (m2 - 6m + 5)x nghịch biến khi hệ số a âm, nghĩa
là: m2 - 6m + 5 < 0 ⇔ (m - 1)(m - 5) < 0 ⇔ 1 < m < 5
Vậy hàm số nghịch biến khi 1 < m < 5
Bài 4. a) Cho hàm số y = f(x) = ax
- Chứng tỏ rằng: f(kx1) = kf(x1)
- Chứng minh rằng: f(x1 + x2) = f(x1) + f(x2)
b) Các hệ thức trên còn đúng với hàm số:
y = f(x) = ax + b, b
Vậy hàm số đồng biến khi m < 1 hoặc m > 5
b) Hàm số y = (m2 - 6m + 5)x nghịch biến khi hệ số a âm, nghĩa
là: m2 - 6m + 5 < 0 ⇔ (m - 1)(m - 5) < 0 ⇔ 1 < m < 5
Vậy hàm số nghịch biến khi 1 < m < 5
Bài 4. a) Cho hàm số y = f(x) = ax
- Chứng tỏ rằng: f(kx1) = kf(x1)
- Chứng minh rằng: f(x1 + x2) = f(x1) + f(x2)
b) Các hệ thức trên còn đúng với hàm số:
y = f(x) = ax + b, b 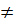 0, hay không?
Giải:
a) * Ta có: f(x) = ax
=> f(kx1) = a(kx1) = k(ax1) = k.f(x1)
Vậy f(kx1) = kf(x1)
* Ta có:
f( x1 + x2) = a( x1 + x2) = ax1 + ax2 = f(x1) + f(x2)
Vậy: f( x1 + x2) = f(x1) + f(x2)
b) Xét hàm số: y = f(x) = ax + b, b
0, hay không?
Giải:
a) * Ta có: f(x) = ax
=> f(kx1) = a(kx1) = k(ax1) = k.f(x1)
Vậy f(kx1) = kf(x1)
* Ta có:
f( x1 + x2) = a( x1 + x2) = ax1 + ax2 = f(x1) + f(x2)
Vậy: f( x1 + x2) = f(x1) + f(x2)
b) Xét hàm số: y = f(x) = ax + b, b 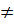 0
Ta có: f(k.x1) = a(k.x1) + b = kax1 + b
kf(x1) = k(ax1 + b) = kax1 + kb
Do đó: f(kx1)
0
Ta có: f(k.x1) = a(k.x1) + b = kax1 + b
kf(x1) = k(ax1 + b) = kax1 + kb
Do đó: f(kx1) 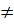 kf(x1) với b
kf(x1) với b 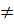 0
Ta có: f(x1 + x2) = a(x1 + x2) + b
f(x1) + f(x2) = (ax1 + b) + (ax2 +b) = a(x1 + x2) + 2b
Do đó: f(x1 + x2)
0
Ta có: f(x1 + x2) = a(x1 + x2) + b
f(x1) + f(x2) = (ax1 + b) + (ax2 +b) = a(x1 + x2) + 2b
Do đó: f(x1 + x2) 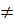 f(x1) + f(x2) với b
f(x1) + f(x2) với b 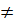 0
Bài 5. a) Khảo sát tính chất và vẽ đồ thị hàm số:
(d): y = (1 -
0
Bài 5. a) Khảo sát tính chất và vẽ đồ thị hàm số:
(d): y = (1 - 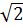 )x +
)x + 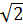 b) Tìm điểm trên (d) có hoành độ 1 +
b) Tìm điểm trên (d) có hoành độ 1 + 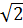 c) Tìm điểm trên (d) có tung độ 2
c) Tìm điểm trên (d) có tung độ 2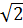 d) Gọi M(xM; yM); N(xN; yN) là các điểm trên (d). Biết XM : XN = 5 : 1; yM + yN = 4. Tìm tọa độ các điểm M, N.
Giải:
d) Gọi M(xM; yM); N(xN; yN) là các điểm trên (d). Biết XM : XN = 5 : 1; yM + yN = 4. Tìm tọa độ các điểm M, N.
Giải:
a) Tập xác định: R
Hàm số y = (1 - 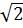 )x + )x + 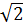 nghịch biến trên R nghịch biến trên R
Đồ thị hàm số y = (1 - 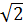 )x + )x + 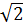 là đường thẳng qua hai điểm: (0; là đường thẳng qua hai điểm: (0; 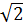 ) và (1, 1) ) và (1, 1)
b) Gọi A (1 + 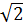 ;yA) là điểm phải tìm. ;yA) là điểm phải tìm. |
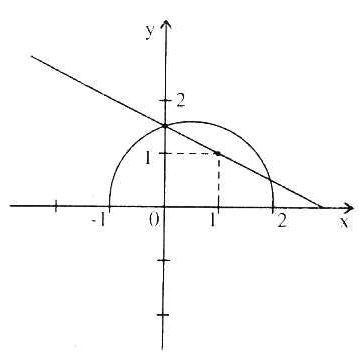 |
Ta có: A 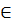 (d) : yA = (1 -
(d) : yA = (1 - 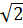 ) (1 +
) (1 + 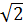 ) +
) + 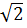 = 1 – 2 +
= 1 – 2 + 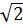 =
= 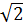 – 1
Vậy A (1 +
– 1
Vậy A (1 + 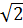 ;
; 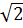 – 1)
c) Gọi B (xB; 2
– 1)
c) Gọi B (xB; 2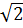 ) là điểm phải tìm.
Ta có: B
) là điểm phải tìm.
Ta có: B 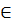 (d): 2
(d): 2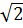 – (1 -
– (1 -  ). xB
⇒ xB =
). xB
⇒ xB = 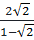 =
= 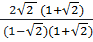 =
= 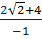 = -2
= -2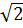 - 4
Vậy B (-2
- 4
Vậy B (-2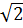 – 4; 2
– 4; 2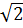 )
d) Ta có: M
)
d) Ta có: M 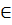 (d): yM = (1 -
(d): yM = (1 - 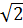 )xM +
)xM + 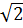 N
N 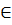 (d): yN = (1 -
(d): yN = (1 - 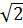 )xN +
)xN + 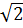 ⇒ yM + yN = (1 -
⇒ yM + yN = (1 - 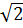 )(xM + xN) + 2
)(xM + xN) + 2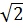 ⇒ 4 = (1 -
⇒ 4 = (1 - 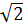 )(xM + xN) + 2
)(xM + xN) + 2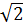 ⇒ xM + xN =
⇒ xM + xN = 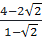 =
= 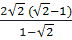 = -2
= -2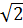 Mà:
Mà: 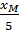 =
= 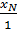 =
= 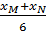 =
= 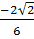 =
= 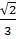 Từ đó suy ra:
* xM =
Từ đó suy ra:
* xM = 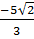 ⇒ yM =
⇒ yM = 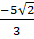 (1 -
(1 - 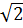 ) +
) + 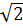 =
= 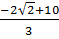 * xN =
* xN = 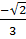 ⇒ yM =
⇒ yM = 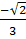 (1 -
(1 - 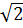 ) +
) + 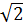 =
= 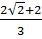 Vậy M
Vậy M 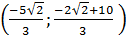 ; N
; N 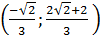 Bài 6. Cho hàm số:
Chứng minh:
a) Hàm số f(x) + g(x) : g(x) - f(x) là hàm số đồng biến.
b) Hàm số f(x) - g(x) là hàm số nghịch biến.
Giải:
a) Ta có: f(x) + g(x) = (a2 + a + 1)x +
Bài 6. Cho hàm số:
Chứng minh:
a) Hàm số f(x) + g(x) : g(x) - f(x) là hàm số đồng biến.
b) Hàm số f(x) - g(x) là hàm số nghịch biến.
Giải:
a) Ta có: f(x) + g(x) = (a2 + a + 1)x + 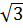 – 1
g(x) – f(x) = (a2 + a + 1) x – 1 -
– 1
g(x) – f(x) = (a2 + a + 1) x – 1 - 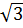 Vì: a2 + a + 1 = a2 + 2.a.
Vì: a2 + a + 1 = a2 + 2.a. +
+  +
+  =
= 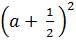 +
+  > 0
> 0 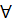 a
Do đó f(x) + g(x); g(x) - f(x) là các hàm số đồng biến
b) Ta có: f(x) - g(x) = (a – a2 + 1)x +
a
Do đó f(x) + g(x); g(x) - f(x) là các hàm số đồng biến
b) Ta có: f(x) - g(x) = (a – a2 + 1)x + 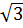 + 1
Vì a – a2 - 1 = (a2 - a + 1 ) =
+ 1
Vì a – a2 - 1 = (a2 - a + 1 ) = 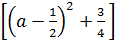 < 0,
< 0,  a
Do đó f(x) – g(x) là hàm số nghịch biến.
Bài 7. 1. Tìm các khoảng mà các hàm số sau đồng biến hoặc nghịch biến trên đó:
a) y = x3 – 3x2 + 2 b) y =
a
Do đó f(x) – g(x) là hàm số nghịch biến.
Bài 7. 1. Tìm các khoảng mà các hàm số sau đồng biến hoặc nghịch biến trên đó:
a) y = x3 – 3x2 + 2 b) y = 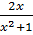 2. Biện luận theo m số nghiệm của các phương trình:
a) x3 - 3x2 + 2 - m = 0 b) mx2 - 2x + m = 0
Giải:
1.a) Tập xác định của hàm số là R
Lấy x1, x2
2. Biện luận theo m số nghiệm của các phương trình:
a) x3 - 3x2 + 2 - m = 0 b) mx2 - 2x + m = 0
Giải:
1.a) Tập xác định của hàm số là R
Lấy x1, x2 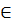 R, x1 < x2 ta có:
y1 =
R, x1 < x2 ta có:
y1 = 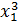 -
- 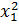 + 2; y2 =
+ 2; y2 = 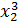 - 3
- 3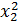 + 2;
Do đó:
+ 2;
Do đó: 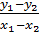 =
= 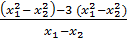 =
= 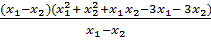 = x1(x1 - 2) + x2(x2 - 2) .
= x1(x1 - 2) + x2(x2 - 2) . 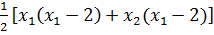 Rõ ràng:
- Nếu x1, x2
Rõ ràng:
- Nếu x1, x2 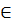 (0;2):
(0;2): 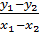 < 0 ⇒ y1 < y2
⇒ Hàm số nghịch biến
- Nếu x1, x2 < 0 hoặc x1, x2 > 2: ⇒
< 0 ⇒ y1 < y2
⇒ Hàm số nghịch biến
- Nếu x1, x2 < 0 hoặc x1, x2 > 2: ⇒ 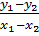 > 0 ⇒ y1 > y2
⇒ Hàm số đồng biến
Vậy: Hàm số nghịch biến trong khoảng (0, 2), đồng biến trong khoảng (-
> 0 ⇒ y1 > y2
⇒ Hàm số đồng biến
Vậy: Hàm số nghịch biến trong khoảng (0, 2), đồng biến trong khoảng (-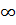 ; 0): (2, +
; 0): (2, +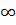 )..
b) Tập xác định của hàm số là R
Lấy x1, x2
)..
b) Tập xác định của hàm số là R
Lấy x1, x2 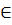 R, x1 < x2 ta có: y1 =
R, x1 < x2 ta có: y1 = 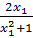 ; y2 =
; y2 = 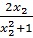 Do đó: y1 – y2 =
Do đó: y1 – y2 = 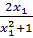 -
- 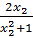 =
= 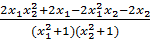 =
= 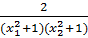 (1- x1x2)(x1- x2)
⇒
(1- x1x2)(x1- x2)
⇒ 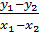 =
= 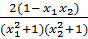 Nếu x1, x2
Nếu x1, x2 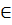 (-1; 1):
(-1; 1): 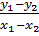 > 0 ⇒ y1 < y2
⇒ Hàm số đồng biến
Nếu: x1, x2 < -1 hoặc x1, x2 > 1
> 0 ⇒ y1 < y2
⇒ Hàm số đồng biến
Nếu: x1, x2 < -1 hoặc x1, x2 > 1
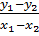 < 0 ⇒ y1 > y2
⇒ Hàm số nghịch biến
Vậy: Hàm số nghịch biến trong các khoảng (-
< 0 ⇒ y1 > y2
⇒ Hàm số nghịch biến
Vậy: Hàm số nghịch biến trong các khoảng (-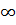 , -1); (1, +
, -1); (1, +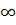 ), đồng biến trong khoảng (-1, 1)
2. a) Bảng biến thiên của hàm số y = x3 - 3x2 + 2
), đồng biến trong khoảng (-1, 1)
2. a) Bảng biến thiên của hàm số y = x3 - 3x2 + 2
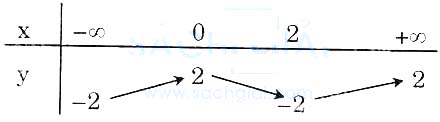 Dựa vào bảng biến thiên này và để ý phương trình đã cho tương đương x3 - 3x2 + 2 = m, ta suy ra:
* m < -2 hoặc m > 2: phương trình có 1 nghiệm.
* m = -2 hoặc m = 2: phương trình có 2 nghiệm.
* -2 < m < 2: phương trình có 3 nghiệm.
b) Bảng biến thiên của hàm số y =
Dựa vào bảng biến thiên này và để ý phương trình đã cho tương đương x3 - 3x2 + 2 = m, ta suy ra:
* m < -2 hoặc m > 2: phương trình có 1 nghiệm.
* m = -2 hoặc m = 2: phương trình có 2 nghiệm.
* -2 < m < 2: phương trình có 3 nghiệm.
b) Bảng biến thiên của hàm số y = 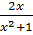
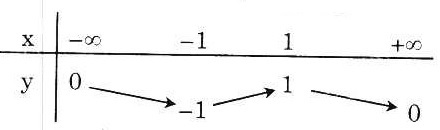 Dựa vào bảng biến thiên này và để ý phương trình đã cho tương đương
Dựa vào bảng biến thiên này và để ý phương trình đã cho tương đương 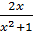 = m, ta suy ra:
* m < -1 hoặc m > 1 : phương trình vô nghiệm.
* m = -1 hoặc m = 1 : phương trình có 1 nghiệm.
* -1 < m < 0 hoặc 0 < m < 1 : phương trình có 2 nghiệm.
* m = 0 phương trình có 1 nghiệm.
= m, ta suy ra:
* m < -1 hoặc m > 1 : phương trình vô nghiệm.
* m = -1 hoặc m = 1 : phương trình có 1 nghiệm.
* -1 < m < 0 hoặc 0 < m < 1 : phương trình có 2 nghiệm.
* m = 0 phương trình có 1 nghiệm.
© Bản quyền thuộc về
Bài kiểm tra. Ghi rõ nguồn Bài kiểm tra.com khi sao chép nội dung này.



