Giải bài tập Toán 9, Luyện tập nhắc lại và bổ sung các khái niệm về hàm số
2019-07-30T12:21:29-04:00
2019-07-30T12:21:29-04:00
Giải bài tập Toán 9, Luyện tập nhắc lại và bổ sung các khái niệm về hàm số
/themes/cafe/images/no_image.gif
Bài Kiểm Tra
https://baikiemtra.com/uploads/bai-kiem-tra-logo.png
Thứ ba - 30/07/2019 04:49
Giải bài tập Toán 9, Luyện tập nhắc lại và bổ sung các khái niệm về hàm số
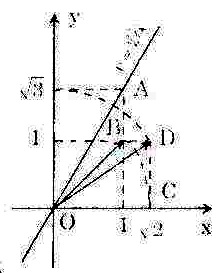
Bài 1. Đồ thị hàm số y = 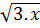 được vẽ bằng compa và thước thẳng ở hình bên được vẽ bằng compa và thước thẳng ở hình bên
Hãy tìm điểm và trình bày lại các bước thực hiện vẽ đồ thị đó. |
 |
Giải:
Quy trình và các bước vẽ:
* Dựng điểm B (1;1) . Khi đó ta có OB = 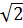 + Lấy O làm tâm, OB làm bán kính, dựng cung
+ Lấy O làm tâm, OB làm bán kính, dựng cung 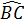 , với C thuộc trục Ox. Khi đó C(
, với C thuộc trục Ox. Khi đó C( 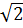 ; 0).
+ Dựng điểm D(
; 0).
+ Dựng điểm D( 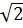 ; 0). Khi đó OD =
; 0). Khi đó OD = 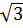 + Lấy O làm tâm, OD làm bán kính, dựng cung
+ Lấy O làm tâm, OD làm bán kính, dựng cung 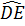 , với E thuộc trục Oy. Khi đó E(0;
, với E thuộc trục Oy. Khi đó E(0; 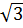 ) dựng điểm A(1;
) dựng điểm A(1; 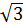 )
+ Nối OA ta dược đường thẳng: y =
)
+ Nối OA ta dược đường thẳng: y = 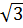 .x .
Ghi chú:
Mục đích qui trình trên là để xác định chính xác điểm A(1;
.x .
Ghi chú:
Mục đích qui trình trên là để xác định chính xác điểm A(1; 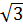 ).
).
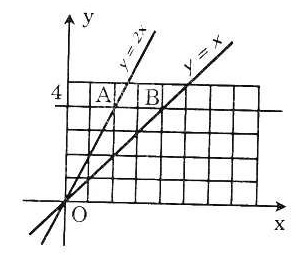
Bài 2. a) Vẽ đồ thị của các hàm số y = x và y = 2x trên cùng một mặt phẳng tọa độ Oxy (h.5).
b) Đường thẳng song song với trục Ox và cắt trục Oy tại điểm có tung độ y = 4 lần lượt cắt các đường thẳng y = 2x, y = x tại hai điểm A và B.
Tìm tọa độ của các điểm A, B và tính chu vi, diện tích  OAB theo đơn vị đo trên các trục tọa độ là xentimét. OAB theo đơn vị đo trên các trục tọa độ là xentimét. |
 |
Giải:
a) 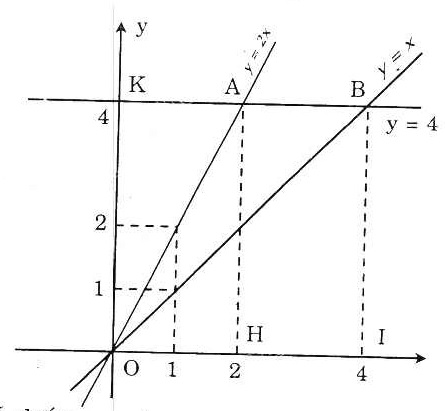 b) * Dễ thấy: yA = 4.
Mặt khác: yA = 2xA ⇒ 4 = 2xA ⇒ XA = 2.
Vậy: A(2, 4)
* Dễ thấy: yB = 4.
Mặt khác: yB = xB ⇒ 4 = XB. Vậy: B(4; 4).
Dựng AH ⊥ Ox. Khi đó: H(2; 0)
BI ⊥ Ox. Khi đó: I(4; 0)
AK ⊥ Oy. Khi đó: K(0; 4)
* Ta có: OH = | xH | = 2
OI = | x1 | = 4
AH = BI = OK = | yK | = 4
* Ta có: OA =
b) * Dễ thấy: yA = 4.
Mặt khác: yA = 2xA ⇒ 4 = 2xA ⇒ XA = 2.
Vậy: A(2, 4)
* Dễ thấy: yB = 4.
Mặt khác: yB = xB ⇒ 4 = XB. Vậy: B(4; 4).
Dựng AH ⊥ Ox. Khi đó: H(2; 0)
BI ⊥ Ox. Khi đó: I(4; 0)
AK ⊥ Oy. Khi đó: K(0; 4)
* Ta có: OH = | xH | = 2
OI = | x1 | = 4
AH = BI = OK = | yK | = 4
* Ta có: OA = 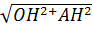 =
= 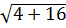 =
= 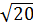 = 2
= 2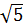 OB =
OB = 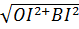 =
= 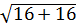 =
= 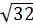 = 4
= 4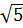 AB = HI = OI – OH = 4 - 2 = 2
Vậy:
AB = HI = OI – OH = 4 - 2 = 2
Vậy:
* chu vi tam giác OAB = OA + OB + AB = 2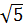 + 4
+ 4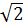 + 2
* Diện tích tam giác OAB =
+ 2
* Diện tích tam giác OAB =  AB. OK =
AB. OK =  .2.4 = 4 (đvdt).
Bài 3. Cho các hàm số y = 0,5x và y = 0,5x + 2.
a) Tính giá trị y tương ứng của mỗi hàm số theo giá trị đã cho của biến x rồi điền vào bảng sau:
.2.4 = 4 (đvdt).
Bài 3. Cho các hàm số y = 0,5x và y = 0,5x + 2.
a) Tính giá trị y tương ứng của mỗi hàm số theo giá trị đã cho của biến x rồi điền vào bảng sau:
| x |
-2,5 |
-2,25 |
-1,5 |
-1 |
0 |
1 |
1,5 |
2,25 |
2,5 |
| y = 0,5x |
|
|
|
|
|
|
|
|
|
| y = 0,5x + 2 |
|
|
|
|
|
|
|
|
|
b) Có nhận xét gì về các giá trị tương ứng của hai hàm số đó khi biến x lấy cùng một giá trị?
Giải:
a) Tính các giá trị của y, ta được:
| x |
-2,5 |
-2,25 |
-1,5 |
-1 |
0 |
1 |
1,5 |
2,25 |
2,5 |
| y = 0,5x |
-1,25 |
-1,125 |
-0,75 |
-0,5 |
0 |
0,5 |
0,75 |
1,125 |
1,25 |
| y = 0,5x + 2 |
0,75 |
0,875 |
1,25 |
1,5 |
2 |
2,5 |
2,75 |
3,125 |
3,25 |
b) Ta nhận thấy rằng giá trị hàm số y = 0,5x + 2 luôn luôn lớn hơn giá trị hàm số y = 0,5x là 2 đơn vị khi x lấy cùng một giá trị.
Bài 4. Cho hàm số y = f(x) = 3x.
Cho x các giá trị thực bất kì x1, x2 sao cho x1 < x2. Hãy chứng minh f(x1) < f(x2) rồi rút ra kết luận hàm số đã cho đồng biến trên tập hợp số thực R.
Giải:
Cho x1, x2 các giá trị thực bất kì sạo cho x1 < x2.
Ứng với giá trị x1 thì hàm số nhận giá trị f(x1) = 3x1.
Ứng với giá trị x2 thì hàm số nhận giá trị f(x2) = 3x2.
Xét hiệu f(x1) - f(x2) = 3x1 – 3x2
⇒ f(x1) - f(x2) = 3(x1 – x2) (1)
Theo giả thiết, x1 < x2. nên x1 – x2 < 0 (2)
Từ (1) và (2) ta suy ra: f(x1) - f(x2) < 0 ⇔ f(x1) < f(x2)
Vậy x1 < x2 ⇒ f(x1) < f(x2) (3)
Vì x1, x2 là hai số thực bất kì nên từ (3) ta kết luận hàm số y = 3x đồng biến trên tập số thực R vì (3) đúng với mọi giá trị bất kì của x 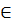 R.
R.
© Bản quyền thuộc về
Bài kiểm tra. Ghi rõ nguồn Bài kiểm tra.com khi sao chép nội dung này.


