Giải bài tập Toán 9, chương II: Bài 4: Đường thẳng song song và đường thẳng cắt nhau
2019-07-31T22:29:04-04:00
2019-07-31T22:29:04-04:00
Giải bài tập Toán 9, chương II: Bài 4: Đường thẳng song song và đường thẳng cắt nhau
/themes/cafe/images/no_image.gif
Bài Kiểm Tra
https://baikiemtra.com/uploads/bai-kiem-tra-logo.png
Thứ tư - 31/07/2019 22:27
Giải bài tập Toán 9, chương II: Bài 4: Đường thẳng song song và đường thẳng cắt nhau
Bài 1. Hãy chỉ ra ba cặp đường thẳng cắt nhau và các cặp đường thẳng song song trong các đường thẳng sau:
a) y = 1,5x + 2; b) y = x + 2; c) y = 0,5x – 3
d) y = x – 3; e) y = 1,5x – 1; g) y = 0,5x + 3
Giải:
- Các đường thẳng cắt nhau là các đường thẳng có a 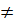 a’. Ta có ba cặp sau:
y = 1,5x + 2 và y = x + 2
y = 1,5x + 2 và y = 0,5x - 3
y = x - 3 và y = 0,5x + 3.
- Các đường thẳng song song là các đường thẳng có a
a’. Ta có ba cặp sau:
y = 1,5x + 2 và y = x + 2
y = 1,5x + 2 và y = 0,5x - 3
y = x - 3 và y = 0,5x + 3.
- Các đường thẳng song song là các đường thẳng có a 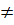 a’ và b
a’ và b 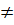 b’. Ta có các cặp sau:
y = 1,5x + 2 và y = 1,5x - 1
y = x + 2 và y = x - 3
y = 0,5x - 3 và y = 0,5x + 3.
Bài 2. Cho hai hàm số bậc nhất y = mx + 3 và y = (2m + 1)x - 5. Tìm giá trị m để đồ thị của hai hàm số đã cho là:
a) Hai đường thẳng song song; b) Hai đường thẳng cắt nhau.
Giải:
a) Hai hàm số y = mx + 3 và y = (2m + 1)x - 5 đã có b
b’. Ta có các cặp sau:
y = 1,5x + 2 và y = 1,5x - 1
y = x + 2 và y = x - 3
y = 0,5x - 3 và y = 0,5x + 3.
Bài 2. Cho hai hàm số bậc nhất y = mx + 3 và y = (2m + 1)x - 5. Tìm giá trị m để đồ thị của hai hàm số đã cho là:
a) Hai đường thẳng song song; b) Hai đường thẳng cắt nhau.
Giải:
a) Hai hàm số y = mx + 3 và y = (2m + 1)x - 5 đã có b 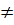 b’
Để đồ thị của chúng là hai đường thẳng song song thì ta phải có m = 2m + 1 ⇒ m = -1.
Trường hợp này ta được hai hàm số y = -x + 3 và y = -x - 5 có đồ thị là các đường thẳng song song và cắt nhau.
b) Để đồ thị của hai hàm số y = mx + 3 và y = (2m + 1 )x - 5 là hai đường thẳng cắt nhau, ta cần có a
b’
Để đồ thị của chúng là hai đường thẳng song song thì ta phải có m = 2m + 1 ⇒ m = -1.
Trường hợp này ta được hai hàm số y = -x + 3 và y = -x - 5 có đồ thị là các đường thẳng song song và cắt nhau.
b) Để đồ thị của hai hàm số y = mx + 3 và y = (2m + 1 )x - 5 là hai đường thẳng cắt nhau, ta cần có a 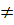 a’ hay m
a’ hay m 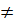 2m + 1 ⇒ m
2m + 1 ⇒ m 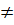 -1.
Bài 3. Cho hàm số y = ax + 3. Hãy xác định hệ số a trong mỗi trường hợp sau:
a) Để đồ thị của hàm số song song với đường thẳng y = -2x.
b) Khi x = 2 thì hàm số có giá trị y = 7.
Giải:
a) Đồ thị của hàm số y = ax + 3 song song với đường thẳng y = -2x khi và chỉ khi:
'
-1.
Bài 3. Cho hàm số y = ax + 3. Hãy xác định hệ số a trong mỗi trường hợp sau:
a) Để đồ thị của hàm số song song với đường thẳng y = -2x.
b) Khi x = 2 thì hàm số có giá trị y = 7.
Giải:
a) Đồ thị của hàm số y = ax + 3 song song với đường thẳng y = -2x khi và chỉ khi:
'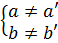 ⇔
⇔ 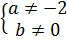 ⇔ a = - 2
b) Khi x = 2 thì hàm số có giá trị y = 7 nên: 7 = a.2 + 3 ⇔ a = 2.
BÀI TẬP LÀM THÊM
Bài 1. Cho hai đường thẳng:
y = ( m + 6) x + 2 và y = m(3m - 4)x - 5.
a) Chứng minh rằng khi m = -2 thì hai đường thẳng đã cho song song với nhau.
b) Tìm tất cả các giá trị của m để hai đường thẳng đã cho song song với nhau.
Giải:
a) Khi m = -2, hai đường thẳng có cùng hệ số góc là 4 nên chúng song song với nhau.
b) Hai đường thẳng y = (m + 6)x + 2 và y = m(3m + 4)x- 5 song song với nhau khi và chỉ khi:
m = 6 – m (3m + 4) ⇔ 3m2 + 3m – 6 = 0
⇔ m2 + m – 2 = 0 ⇔ (m - 1)(m + 2) = 0
⇔
⇔ a = - 2
b) Khi x = 2 thì hàm số có giá trị y = 7 nên: 7 = a.2 + 3 ⇔ a = 2.
BÀI TẬP LÀM THÊM
Bài 1. Cho hai đường thẳng:
y = ( m + 6) x + 2 và y = m(3m - 4)x - 5.
a) Chứng minh rằng khi m = -2 thì hai đường thẳng đã cho song song với nhau.
b) Tìm tất cả các giá trị của m để hai đường thẳng đã cho song song với nhau.
Giải:
a) Khi m = -2, hai đường thẳng có cùng hệ số góc là 4 nên chúng song song với nhau.
b) Hai đường thẳng y = (m + 6)x + 2 và y = m(3m + 4)x- 5 song song với nhau khi và chỉ khi:
m = 6 – m (3m + 4) ⇔ 3m2 + 3m – 6 = 0
⇔ m2 + m – 2 = 0 ⇔ (m - 1)(m + 2) = 0
⇔ 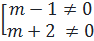 ⇔
⇔ 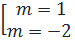 Bài 2. Cho đường thẳng D: y = kx + 1.
Xác định phương trình của D trong các trường hợp sau:
a ) D song song với D’: y = x
b) D cùng phương với D1: y = -2x + 2005
c) D vuông góc với D2: y = 2x + 1
d) D vuông góc với D3: y = - x - 1
Giải:
a) D // D’ ⇔ k = k’⇒ k = 1
⇒ Phương trình của D là: y = x + 1
b) D cùng phương với D1 ⇔ k = k’ = -2
⇒ Phương trình của D là: y = -2x + 1
c) D ⊥ D2 ⇔ k.k’ = -1 ⇔ k.2 = -1 ⇔ k = -
Bài 2. Cho đường thẳng D: y = kx + 1.
Xác định phương trình của D trong các trường hợp sau:
a ) D song song với D’: y = x
b) D cùng phương với D1: y = -2x + 2005
c) D vuông góc với D2: y = 2x + 1
d) D vuông góc với D3: y = - x - 1
Giải:
a) D // D’ ⇔ k = k’⇒ k = 1
⇒ Phương trình của D là: y = x + 1
b) D cùng phương với D1 ⇔ k = k’ = -2
⇒ Phương trình của D là: y = -2x + 1
c) D ⊥ D2 ⇔ k.k’ = -1 ⇔ k.2 = -1 ⇔ k = -  ⇒ Phương trình của D là: y = -
⇒ Phương trình của D là: y = -  x + 1
d) D ⊥ D3 ⇔ k.k’ = 1 ⇔ k.-
x + 1
d) D ⊥ D3 ⇔ k.k’ = 1 ⇔ k.-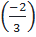 = 1 ⇔ k =
= 1 ⇔ k =  ⇒ Phương trình của D là: y =
⇒ Phương trình của D là: y =  x + 1
Bài 3. Tìm các giá trị của m đế hai đường thẳng:
mx + (m - 1)y - 2(m + 2) = 0 (1)
3mx - (3m + 1)y - (5m + 4) = 0 (2)
a) Song song với nhau. b) Cắt nhau. c) Vuông góc với nhau.
Giải:
Viết lại hai đường thẳng đã cho về dạng y = ax + b:
y =
x + 1
Bài 3. Tìm các giá trị của m đế hai đường thẳng:
mx + (m - 1)y - 2(m + 2) = 0 (1)
3mx - (3m + 1)y - (5m + 4) = 0 (2)
a) Song song với nhau. b) Cắt nhau. c) Vuông góc với nhau.
Giải:
Viết lại hai đường thẳng đã cho về dạng y = ax + b:
y = 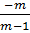 x +
x + 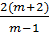 ; (m
; (m 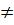 1) (1)
y =
1) (1)
y = 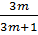 x -
x - 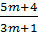 ; (m
; (m 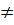 -
-  ) (2)
a) Hai đường thẳng song song
⇔
) (2)
a) Hai đường thẳng song song
⇔ 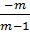 .
. 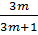 ⇔ m = 0 hoặc m =
⇔ m = 0 hoặc m =  Khi m= 0 thì các đường thẳng (1) và (2) trở thành y = - 4 và y = - 4, hai đường thẳng này trùng nhau.
Khi m =
Khi m= 0 thì các đường thẳng (1) và (2) trở thành y = - 4 và y = - 4, hai đường thẳng này trùng nhau.
Khi m =  . các đường thẳng (1) và (2) trở thành y = -
. các đường thẳng (1) và (2) trở thành y = -  x – 7 và y = -
x – 7 và y = -  x -
x - 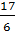 . hai đường thẳng này song song.
b) Hai đường thẳng vuông góc
⇔
. hai đường thẳng này song song.
b) Hai đường thẳng vuông góc
⇔ 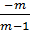 .
. 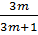 = -1 ⇔ m = -
= -1 ⇔ m = -  c) Hai đường thẳng đã cho cắt nhau khi chúng không song song và không trùng nhau, từ đó suy ra m
c) Hai đường thẳng đã cho cắt nhau khi chúng không song song và không trùng nhau, từ đó suy ra m 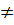 0; m
0; m 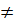
 Bài 4. Tìm giá trị của k đồ ba đường thẳng:
y = -2x + 3 (d1)
y = 3x - 2 (d2)
y = kx + k - 5 (d3)
đồng quy trong mặt phẳng tọa độ.
Giải:
Hai đường thẳng (d1) và (d2) có hệ số của x khác nhau (-2
Bài 4. Tìm giá trị của k đồ ba đường thẳng:
y = -2x + 3 (d1)
y = 3x - 2 (d2)
y = kx + k - 5 (d3)
đồng quy trong mặt phẳng tọa độ.
Giải:
Hai đường thẳng (d1) và (d2) có hệ số của x khác nhau (-2 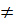 3) nên chúng cắt nhau tại điểm M trong mặt phẳng tọa độ. Khi đó tọa độ của điểm M phải thỏa mãn đồng thời hai phương trình: y = -2x + 3 và y = 3x - 2
Suy ra: -2x + 3 = 3x - 2 ⇔ -5x = -5 ⇔ x = 1
y = -2x + 3 = -2.1 +3 = 1
Tọa độ của điểm M là M( 1; 1)
Để ba đường thẳng đồng quy thì đường thẳng (d1) phải đi qua M( 1; 1 ).
Do đó, ta có: k. 1 + k - 5 = 1 ⇔ 2k = 6 ⇔ k = 3.
Vậy ba dường thẳng (d1), (d2), (d3) đồng quy khi k = 3.
Bài 5. a) Tìm tọa độ giao điểm của hai đường thẳng (d): y = 2x - 3 và (d’): y = x - 1
b) Chứng tỏ ba đường thẳng (d): y = 2x - 3;
(d’): y = x - 1 ; (d’’): y =
3) nên chúng cắt nhau tại điểm M trong mặt phẳng tọa độ. Khi đó tọa độ của điểm M phải thỏa mãn đồng thời hai phương trình: y = -2x + 3 và y = 3x - 2
Suy ra: -2x + 3 = 3x - 2 ⇔ -5x = -5 ⇔ x = 1
y = -2x + 3 = -2.1 +3 = 1
Tọa độ của điểm M là M( 1; 1)
Để ba đường thẳng đồng quy thì đường thẳng (d1) phải đi qua M( 1; 1 ).
Do đó, ta có: k. 1 + k - 5 = 1 ⇔ 2k = 6 ⇔ k = 3.
Vậy ba dường thẳng (d1), (d2), (d3) đồng quy khi k = 3.
Bài 5. a) Tìm tọa độ giao điểm của hai đường thẳng (d): y = 2x - 3 và (d’): y = x - 1
b) Chứng tỏ ba đường thẳng (d): y = 2x - 3;
(d’): y = x - 1 ; (d’’): y =  đồng quy.
Giải:
a) Gọi M( x0;y0) là giao điểm của (d) và (d’).
Ta có:
M
đồng quy.
Giải:
a) Gọi M( x0;y0) là giao điểm của (d) và (d’).
Ta có:
M 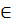 (d); y0 = 2x0 - 3 (1 )
M
(d); y0 = 2x0 - 3 (1 )
M 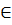 (d’): y0 = x0 - 1 (2)
(1 ) và (2): 2x0 - 3 = x0 - 1 ⇔ x0 = 2
x0 = 2 ⇒ y0 = 2 - 1 = 1
Vậy tọa độ giao điểm của (d) và (d’) là (2; 1)
b) (d) và (d’) cắt nhau tại M(2; 1)
M
(d’): y0 = x0 - 1 (2)
(1 ) và (2): 2x0 - 3 = x0 - 1 ⇔ x0 = 2
x0 = 2 ⇒ y0 = 2 - 1 = 1
Vậy tọa độ giao điểm của (d) và (d’) là (2; 1)
b) (d) và (d’) cắt nhau tại M(2; 1)
M 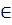 (d”) : 1 =
(d”) : 1 =  ⇔ 1 = 1 (đẳng thức đúng)
Vậy (d), (d’), (d”) đồng quy tại M.
Bài 6. Cho hai đường thẳng:
y = ( m + 1) x - 3 và y = (2m - 1) x + 4
a) Chứng minh rằng khi m thì hai đường thẳng đã cho vuông góc với nhau.
b) Tìm tất cả các giá trị của m để hai đường thẳng đã cho vuông góc với nhau.
Giải:
a) Khi m = -
⇔ 1 = 1 (đẳng thức đúng)
Vậy (d), (d’), (d”) đồng quy tại M.
Bài 6. Cho hai đường thẳng:
y = ( m + 1) x - 3 và y = (2m - 1) x + 4
a) Chứng minh rằng khi m thì hai đường thẳng đã cho vuông góc với nhau.
b) Tìm tất cả các giá trị của m để hai đường thẳng đã cho vuông góc với nhau.
Giải:
a) Khi m = -  thì hai đường thẳng y = (m + 1)x - 3 và y = (2m - 1)x + 4 có hệ số góc lần lượt là a =
thì hai đường thẳng y = (m + 1)x - 3 và y = (2m - 1)x + 4 có hệ số góc lần lượt là a =  ; a’ = - 2, khi đó aa’ =
; a’ = - 2, khi đó aa’ =  (-2) = -1.
Vậy hai dường thẳng vuông góc với nhau.
b) Hai đường thẳng y = (m + 1)x - 3 và y = (2m - 1)x + 4 vuông góc với nhau khi và chỉ khi:
(m + 1)(2m - 1) = - 1 ⇔ 2m2 + m = 0 ⇔ m (2m + 1) = 0
⇔
(-2) = -1.
Vậy hai dường thẳng vuông góc với nhau.
b) Hai đường thẳng y = (m + 1)x - 3 và y = (2m - 1)x + 4 vuông góc với nhau khi và chỉ khi:
(m + 1)(2m - 1) = - 1 ⇔ 2m2 + m = 0 ⇔ m (2m + 1) = 0
⇔ 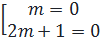 ⇔
⇔ 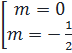
© Bản quyền thuộc về
Bài kiểm tra. Ghi rõ nguồn Bài kiểm tra.com khi sao chép nội dung này.