Giải bài tập Toán 9, chương IV, bài 2: Đồ thị của hàm số y = ax2 (a ≠ 0).
2019-08-23T04:43:37-04:00
2019-08-23T04:43:37-04:00
Giải bài tập Toán 9, chương IV, bài 2: Đồ thị của hàm số y = ax2 (a ≠ 0): Tóm tắt kiến thức, ví dụ, hướng dẫn giải bài tập trong sách giáo khoa và bài tập luyện thêm.
/themes/cafe/images/no_image.gif
Bài Kiểm Tra
https://baikiemtra.com/uploads/bai-kiem-tra-logo.png
Thứ sáu - 23/08/2019 04:42
Giải bài tập Toán 9, chương IV, bài 2: Đồ thị của hàm số y = ax2 (a ≠ 0): Tóm tắt kiến thức, ví dụ, hướng dẫn giải bài tập trong sách giáo khoa và bài tập luyện thêm.
A. Tóm tắt kiến thức
Đồ thị của hàm số y = ax2 (a 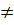 0) là một đường cong đi qua gốc toạ độ và nhận trục Oy làm trục đối xứng. Đường cong đó gọi là một parabol với đỉnh O.
- Nếu a > 0 thì đồ thi nằm phía trên trục hoành và O là điểm thấp nhất của đồ thị.
- Nếu a < 0 thì đồ thị nằm phía dưới trục hoành và O là điểm cao nhất của đồ thị.
Lưu ý. Vì tính đối xứng của đồ thị qua trục Oy nên khi vẽ đồ thị ta chỉ cần xác định một số điểm ở bên phải trục Oy rồi lấy các điểm lần lượt đối xứng với chúng qua trục Oy.
B. Ví dụ
0) là một đường cong đi qua gốc toạ độ và nhận trục Oy làm trục đối xứng. Đường cong đó gọi là một parabol với đỉnh O.
- Nếu a > 0 thì đồ thi nằm phía trên trục hoành và O là điểm thấp nhất của đồ thị.
- Nếu a < 0 thì đồ thị nằm phía dưới trục hoành và O là điểm cao nhất của đồ thị.
Lưu ý. Vì tính đối xứng của đồ thị qua trục Oy nên khi vẽ đồ thị ta chỉ cần xác định một số điểm ở bên phải trục Oy rồi lấy các điểm lần lượt đối xứng với chúng qua trục Oy.
B. Ví dụ
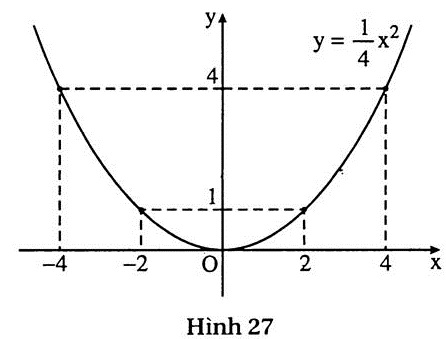
Ví dụ 1. Vẽ đồ thị của hàm số y =  x2. x2.
Giải: Lập bảng một số giá trị tương ứng của x và y:
| x |
- 4 |
- 2 |
- 1 |
0 |
1 |
2 |
4 |
y =  x2 x2 |
4 |
1 |
 |
0 |
 |
1 |
4 |
(h.27) là đồ thị của hàm số y =  x2 x2
|
|
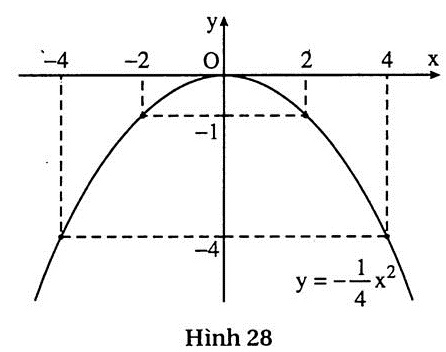
Ví dụ 2. Vẽ đồ thị của hàm số y = 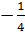 x2. x2.
Giải: Lập bảng một số giá trị tương ứng của x và y:
| x |
- 4 |
- 2 |
- 1 |
0 |
1 |
2 |
4 |
y = 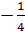 x2 x2 |
- 4 |
- 1 |
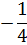 |
0 |
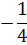 |
-1 |
- 4 |
(h.28) là đồ thị của hàm số y = 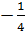 x2 x2 |
|
Ví dụ 3. Xác định giá trị hệ số a của hàm số y = ax2 biết rằng đồ thị của nó đi qua điểm M(-0,5 ; 3).
Giải. Vì M(-0,5 ; 3) thuộc đồ thị của hàm số y = ax2 nên 3 = a.(-0,5)2 hay 0,25a = 3.
Do đó a = 3 : 0,25. Vậy a = 12.
Ví dụ 4. Đồ thị của hàm số y = ax2, đi qua điểm M(2 ; -5). Hỏi những điểm nào sau đây thuộc đồ thị của nó ?
N(4 ;-20) ; b) P(-2;-5); c)Q(-3;10).
❖ Phân tích. Muốn biết một điểm có thuộc đồ thị của hàm số hay không ta cần kiểm tra xem toạ độ của điểm đó có thoả mãn đẳng thức xác định hàm số đó hay không. Vì thế trước hết ta cần xác định hệ số a.
Giải.
Vì đồ thị của hàm số đi qua điểm M(2 ; -5) nên -5 = a.22 .
Do đó a = 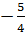 và hàm số đã cho là y =
và hàm số đã cho là y = 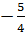 x2 .
a) Với x = 4 thì y =
x2 .
a) Với x = 4 thì y = 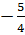 . 42 = -20.
Vậy N thuộc đồ thị của hàm số.
b) Với x = -2 thì y =
. 42 = -20.
Vậy N thuộc đồ thị của hàm số.
b) Với x = -2 thì y =  .(-2)2 = - 5.
Vậy P thuộc đồ thị của hàm số.
c) Với x = -3 thì y =
.(-2)2 = - 5.
Vậy P thuộc đồ thị của hàm số.
c) Với x = -3 thì y = 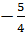 .(-3)2 =
.(-3)2 = 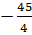
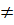 10.
Vậy Q không thuộc đồ thị của hàm số.
C. Hướng dẫn giải bài tập trong sách giáo khoa
4.
10.
Vậy Q không thuộc đồ thị của hàm số.
C. Hướng dẫn giải bài tập trong sách giáo khoa
4.
| x |
-2 |
-1 |
0 |
1 |
2 |
y =  x2 x2 |
6 |
 |
0 |
 |
6 |
| x |
-2 |
-1 |
0 |
1 |
2 |
y = 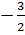 x2 x2 |
- 6 |
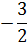 |
0 |
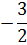 |
- 6 |
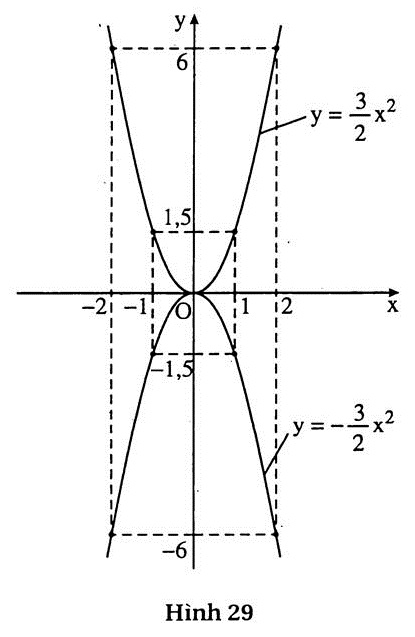
| (h.29) Hai đồ thị đối xứng với nhau qua trục Ox. Thật vậy, hai điểm (1 ; 1,5) và (1 ; -1,5) đối xứng với nhau qua Ox. Tương tự : các cặp điểm (-1 ; 1,5) và (-1 ; -1,5); (2 ; 6) và (2 ; -6) ; (-2 ; 6) và (-2 ; -6) đối xứng với nhau qua Ox. |
|
Hướng dẫn.
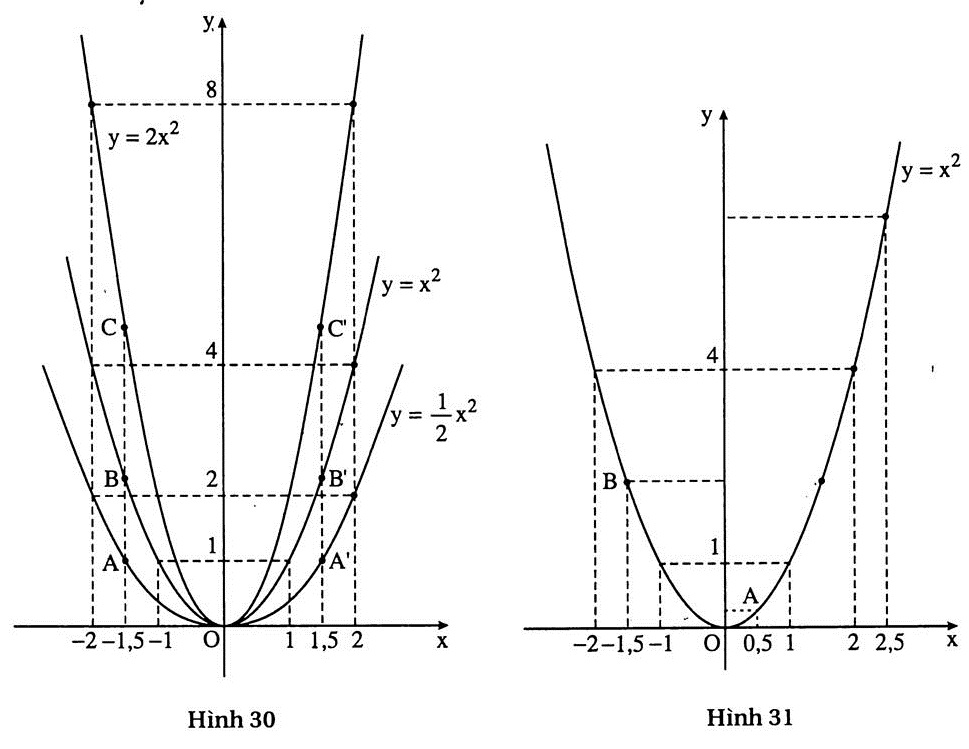
a) (h.30).
b) Tung độ của A là  , của B là
, của B là  , của C là
, của C là  d) Các hàm số đã cho đều có giá trị nhỏ nhất là 0.
6. a) Đồ thị hàm số (h.31).
Đáp số: b) f(-8) = 64 ; f(-1,3) = 1,69;
f(-0,75) = 0,4225 ; f(l,5) = 2,25.
c) (0,5)2 =
d) Các hàm số đã cho đều có giá trị nhỏ nhất là 0.
6. a) Đồ thị hàm số (h.31).
Đáp số: b) f(-8) = 64 ; f(-1,3) = 1,69;
f(-0,75) = 0,4225 ; f(l,5) = 2,25.
c) (0,5)2 =  .
Đó là tung độ của điểm A trên đồ thị có hoành độ bằng 0,5.
(-1,5)2 là tung độ của điểm B trên đồ thị (h.31).
Do đó (-1,5)2 = 2
.
Đó là tung độ của điểm A trên đồ thị có hoành độ bằng 0,5.
(-1,5)2 là tung độ của điểm B trên đồ thị (h.31).
Do đó (-1,5)2 = 2 .
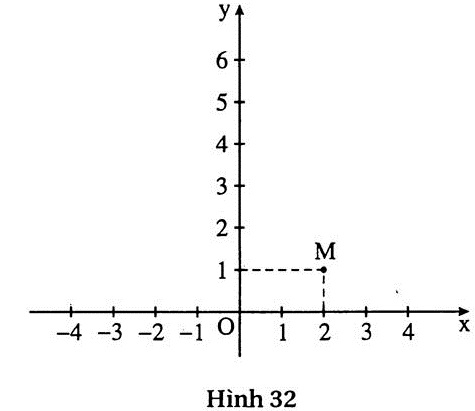
7. Giải, a) Điểm M(2 ; 1) (h.32) thuộc đồ thị nên 1 = a.22 = 4a.
Do đó a =
.
7. Giải, a) Điểm M(2 ; 1) (h.32) thuộc đồ thị nên 1 = a.22 = 4a.
Do đó a =  . .
b) Khi x = 4 thì y =
. .
b) Khi x = 4 thì y =  .42 = 4.
Vậy điểm A(4 ; 4) thuộc đồ thị.
c) Chỉ cần lấy thêm hai điểm M’ và A’ lần lượt đối xứng với M và A qua Oy.
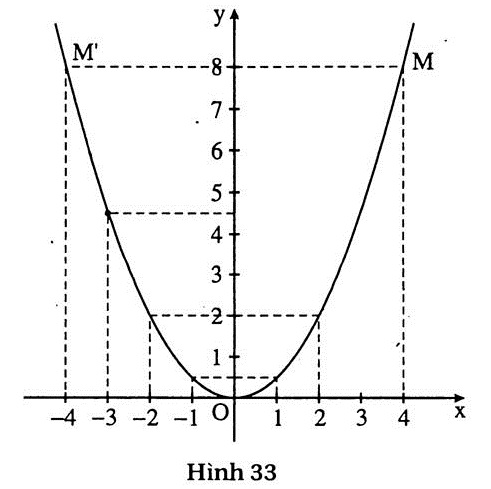
8. Trả lời : (h.33) a) a =
.42 = 4.
Vậy điểm A(4 ; 4) thuộc đồ thị.
c) Chỉ cần lấy thêm hai điểm M’ và A’ lần lượt đối xứng với M và A qua Oy.
8. Trả lời : (h.33) a) a =  . .
b) Tung độ của điểm thuộc parabol có hoành độ x = -3 là 4,5.
c) Đó là điểm M(4 ; 8) và M’(-4 ; 8).
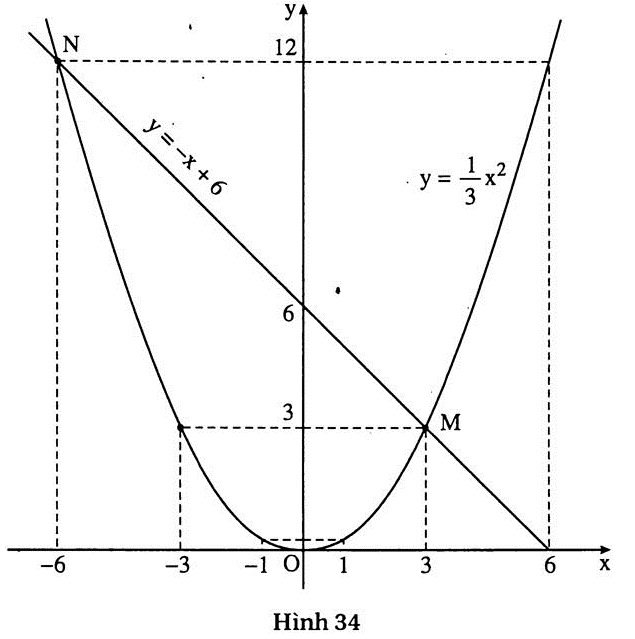
9. Giải: a) Đồ thị (h.34)
b) Toạ độ các giao điểm của hai đồ thị là : M(3 ; 3), N(-6 ; 12).
. .
b) Tung độ của điểm thuộc parabol có hoành độ x = -3 là 4,5.
c) Đó là điểm M(4 ; 8) và M’(-4 ; 8).
9. Giải: a) Đồ thị (h.34)
b) Toạ độ các giao điểm của hai đồ thị là : M(3 ; 3), N(-6 ; 12).
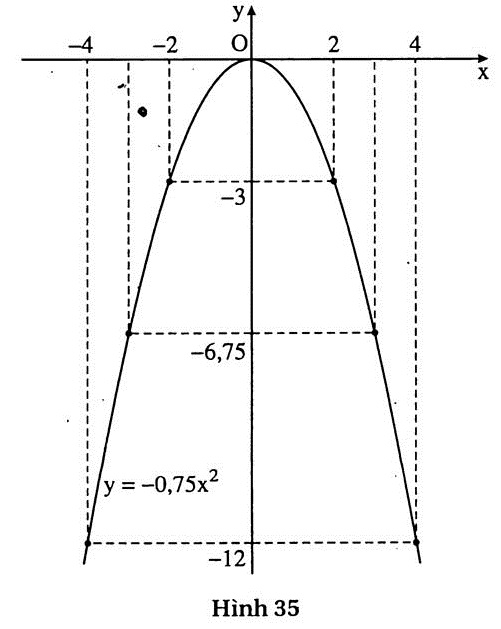
10. Trả lời : (h.35).
Khi x tăng từ -2 đến 4 thì :
Giá trị lớn nhất của y là 0.
Giá trị nhỏ nhất của y là -12. |
|
D. Bài tập luyện thêm
1. Cho hàm số y = f(x) = ax2 . Đồ thị của nó đi qua điểm A(2 ; -1):
a) Xác định hệ số a.
b) Vẽ đồ thị của hàm số ứng với giá trị vừa tìm được của a.
c) Chứng tỏ rằng điểm M -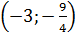 thuộc đồ thị. Tìm trên đồ thị điểm M’ có tung độ là
thuộc đồ thị. Tìm trên đồ thị điểm M’ có tung độ là 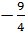 và xác định hoành độ của M’.
d) Không làm tính, dùng tính đồng biến, nghịch biến của hàm số hãy so sánh f(-
và xác định hoành độ của M’.
d) Không làm tính, dùng tính đồng biến, nghịch biến của hàm số hãy so sánh f(-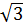 )và f(-1).
2. Cho hàm số y = -4,5x2. Tìm giá trị nhỏ nhất và giá trị lớn nhất của y :
a) Khi -3
)và f(-1).
2. Cho hàm số y = -4,5x2. Tìm giá trị nhỏ nhất và giá trị lớn nhất của y :
a) Khi -3 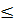 x
x 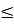 -1 ;
b) Khi -1
-1 ;
b) Khi -1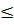 x
x 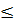 3.
3. Cho hai hàm số: y =
3.
3. Cho hai hàm số: y =  x2 và y =
x2 và y =  x - 1
a) Vẽ đồ thị của hai hàm số này trên cùng một mặt phẳng tọa độ.
b) Tìm tọa độ các giao điểm của hai đồ thị.
c) Dùng cách giải phương trình tích để giải phương trình:
x - 1
a) Vẽ đồ thị của hai hàm số này trên cùng một mặt phẳng tọa độ.
b) Tìm tọa độ các giao điểm của hai đồ thị.
c) Dùng cách giải phương trình tích để giải phương trình:  x2 =
x2 =  x – 1 rồi so sánh các nghiệm tìm được với các hoành độ của hai giao điểm trong câu b.
Hướng dẫn - Đáp số
1. Trả lời: a) a =
x – 1 rồi so sánh các nghiệm tìm được với các hoành độ của hai giao điểm trong câu b.
Hướng dẫn - Đáp số
1. Trả lời: a) a = 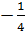 c) Điểm M thuộc đồ thị hàm số y =
c) Điểm M thuộc đồ thị hàm số y = 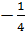 x2 . Điếm M’ có hoành độ là 3.
d) f(-
x2 . Điếm M’ có hoành độ là 3.
d) f(-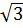 ) < f(-1).
2. Giải. a) Vì a = - 4,5 < 0 nên hàm số đồng biến khi x < 0.
Do đó khi -3
) < f(-1).
2. Giải. a) Vì a = - 4,5 < 0 nên hàm số đồng biến khi x < 0.
Do đó khi -3 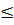 x
x 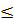 -1 thì f(-3)
-1 thì f(-3) 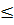 f(x)
f(x) 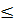 f(-1).
Vì thế giá trị nhỏ nhất của y là f(-3) = -4,5.(-3)2 = - 40,5.
Giá trị lớn nhất của y là : f(-1) = - 4,5.
b) Vì hàm số đồng biến khi x < 0 nên khi (-1)
f(-1).
Vì thế giá trị nhỏ nhất của y là f(-3) = -4,5.(-3)2 = - 40,5.
Giá trị lớn nhất của y là : f(-1) = - 4,5.
b) Vì hàm số đồng biến khi x < 0 nên khi (-1) 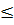 x
x 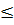 0 thì f(-1)
0 thì f(-1) 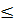 f(x)
f(x) 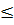 f(0).
Vì hàm số nghịch biến khi x > 0 nên khi 0
f(0).
Vì hàm số nghịch biến khi x > 0 nên khi 0 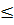 x
x 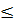 3 thì f(0)
3 thì f(0) 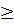 f(x)
f(x) 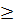 f(3) và f(1) > f(3)
Do đó khi -1
f(3) và f(1) > f(3)
Do đó khi -1 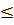 x
x 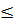 3 thì giá trị lớn nhất của y là f(0) = 0.
Vì f(-1) = f(1) nên f(-1) > f(3).
Do đó khi -1
3 thì giá trị lớn nhất của y là f(0) = 0.
Vì f(-1) = f(1) nên f(-1) > f(3).
Do đó khi -1 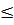 x
x 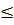 3 thì giá trị nhỏ nhất của y là f(3) = -40,5.
3. Trả lời: b) Toạ độ các giao điểm của hai đồ thị là : M
3 thì giá trị nhỏ nhất của y là f(3) = -40,5.
3. Trả lời: b) Toạ độ các giao điểm của hai đồ thị là : M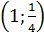 ; N(4 ; 4).
c) Ta có :
; N(4 ; 4).
c) Ta có :  x2 =
x2 =  x - 1 ⇔ x2 = 5x - 4 ⇔ x2 - 5x + 4 = 0
⇔ x2 - x - 4x + 4 = 0 ⇔ (x2 - x) - (4x - 4) = 0 ⇔ x(x - 1) - 4(x - 1) = 0
⇔ (x - 1)(x - 4) = 0 ⇔ x = 1 hoặc x = 4.
Các nghiệm tìm được lần lượt là hoành độ của M và N.
x - 1 ⇔ x2 = 5x - 4 ⇔ x2 - 5x + 4 = 0
⇔ x2 - x - 4x + 4 = 0 ⇔ (x2 - x) - (4x - 4) = 0 ⇔ x(x - 1) - 4(x - 1) = 0
⇔ (x - 1)(x - 4) = 0 ⇔ x = 1 hoặc x = 4.
Các nghiệm tìm được lần lượt là hoành độ của M và N.
© Bản quyền thuộc về
Bài kiểm tra. Ghi rõ nguồn Bài kiểm tra.com khi sao chép nội dung này.