Giải bài tập Toán 9, chương IV, bài 1: Hàm số y = ax2 (a ≠ 0). Phương trình bậc hai một ẩn
2019-08-23T03:58:49-04:00
2019-08-23T03:58:49-04:00
Giải bài tập Toán 9, chương IV, bài 1: Hàm số y = ax2 (a ≠ 0). Phương trình bậc hai một ẩn: Tóm tắt kiến thức, ví dụ, hướng dẫn giải bài tập trong sách giáo khoa và bài tập luyện thêm.
/themes/cafe/images/no_image.gif
Bài Kiểm Tra
https://baikiemtra.com/uploads/bai-kiem-tra-logo.png
Thứ sáu - 23/08/2019 03:53
Giải bài tập Toán 9, chương IV, bài 1: Hàm số y = ax2 (a ≠ 0). Phương trình bậc hai một ẩn: Tóm tắt kiến thức, ví dụ, hướng dẫn giải bài tập trong sách giáo khoa và bài tập luyện thêm.
A. Tóm tắt kiến thức
Tính chất của hàm số y = ax2 (a 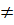 0)
Nếu a > 0 thì hàm số nghịch biến khi x < 0 và đồng biến khi x > 0
Nếu a < 0 thì hàm số đồng biến khi x < 0 và nghịch biến khi x > 0
Nhận xét
Nếu a > 0 thì y > 0 với mọi x
0)
Nếu a > 0 thì hàm số nghịch biến khi x < 0 và đồng biến khi x > 0
Nếu a < 0 thì hàm số đồng biến khi x < 0 và nghịch biến khi x > 0
Nhận xét
Nếu a > 0 thì y > 0 với mọi x 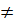 0 ; y = 0 khi x = 0. Giá trị nhỏ nhất của hàm số là y = 0.
Nếu a < 0 thì y < 0 với mọi x
0 ; y = 0 khi x = 0. Giá trị nhỏ nhất của hàm số là y = 0.
Nếu a < 0 thì y < 0 với mọi x 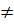 0 ;y = 0 khi x = 0. Giá trị lớn nhất của hàm số là y = 0.
B. Ví dụ
Ví dụ 1. Cho hàm số y =
0 ;y = 0 khi x = 0. Giá trị lớn nhất của hàm số là y = 0.
B. Ví dụ
Ví dụ 1. Cho hàm số y = 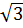 x2. Điền các số thích hợp vào bảng sau :
x2. Điền các số thích hợp vào bảng sau :
| x |
-2 |
-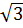 |
-1 |
0 |
1 |
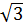 |
2 |
| y |
|
|
|
|
|
|
|
Giải. Với x = -2, y = 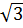 ,(-2)2 = 4
,(-2)2 = 4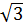 .
Vì bình phương của hai số đối nhau thì bằng nhau nên với x = 2, ta cũng có y = 4
.
Vì bình phương của hai số đối nhau thì bằng nhau nên với x = 2, ta cũng có y = 4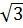 .
Với x =
.
Với x = 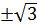 thì y =
thì y = 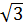 .(
.( 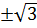 )2 = 3
)2 = 3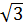 Với x =
Với x = 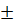 1 thì y =
1 thì y = 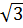 .(
.(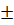 1)2 =
1)2 = 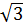 Với x = 0 thì y =
Với x = 0 thì y = 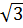 .02 = 0.
Vậy ta có bảng :
.02 = 0.
Vậy ta có bảng :
| x |
-2 |
-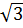 |
-1 |
0 |
1 |
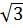 |
2 |
| y |
4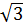 |
3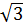 |
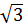 |
0 |
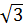 |
3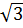 |
4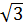 |
Ví dụ 2. Người ta cũng thường kí hiệu hàm số của biến số x bởi f(x) ; chăng hạn, f(x) = 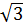 x2.
Bây giờ cho hàm số f(x) =
x2.
Bây giờ cho hàm số f(x) = 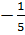 x2 . Hãy tính các giá trị:
f(-5); f
x2 . Hãy tính các giá trị:
f(-5); f 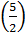 ; f(-0,5).
Không cần tính toán viết -ngay các giá trị : f(5); f
; f(-0,5).
Không cần tính toán viết -ngay các giá trị : f(5); f 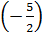 f(0,5). Vì sao có thể làm như thế ?
Giải.
f(-5) =
f(0,5). Vì sao có thể làm như thế ?
Giải.
f(-5) = 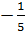 .(-5)2 =
.(-5)2 = 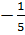 .25 = -5;
f
.25 = -5;
f 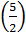 =
= 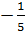 .
.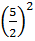 =
= 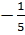 .
. 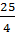 =
= 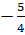 ;
f(-0,5) =
;
f(-0,5) = 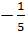 .(-0,5)2 =
.(-0,5)2 = 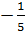 . 0,25 = - 0,05.
Vì bình phương hai số đối nhau thì bằng nhau nên:
f(5) = -5 ; f
. 0,25 = - 0,05.
Vì bình phương hai số đối nhau thì bằng nhau nên:
f(5) = -5 ; f 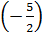 =
= 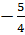 ; f(0,5) = -0,05.
Ví dụ 3. Tìm hàm số y = ax2 trong mỗi trường hợp sau :
Khi x = 5 thì y = - 100 ;
Khi y = 9 thì x = -2.
Giải. a) Vì khi x = 5 thì y = -100 nên -100 = a.52 hay 25a = - 100.
Do đó a = -100 : 25 hay a = -4.
Vậy hàm số cần tìm là y = - 4x .
b) Vì khi y = 9 thì x = - 2 nên 9 = a. (-2)2 hay 4a = 9.
Do đó a =
; f(0,5) = -0,05.
Ví dụ 3. Tìm hàm số y = ax2 trong mỗi trường hợp sau :
Khi x = 5 thì y = - 100 ;
Khi y = 9 thì x = -2.
Giải. a) Vì khi x = 5 thì y = -100 nên -100 = a.52 hay 25a = - 100.
Do đó a = -100 : 25 hay a = -4.
Vậy hàm số cần tìm là y = - 4x .
b) Vì khi y = 9 thì x = - 2 nên 9 = a. (-2)2 hay 4a = 9.
Do đó a =  .
Vậy hàm số cần tìm là y =
.
Vậy hàm số cần tìm là y =  x2.
Ví dụ 4. Xét tính đồng biến, nghịch biến của các hàm số sau :
y = 0,12x2; b)y = -2012x2;
y = (1-
x2.
Ví dụ 4. Xét tính đồng biến, nghịch biến của các hàm số sau :
y = 0,12x2; b)y = -2012x2;
y = (1- 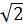 )x2 ; d) y = (2 -
)x2 ; d) y = (2 - 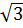 )x2.
Giải. a) Vì 0,12 > 0 nên hàm số y = 0,12x2 nghịch biến khi x < 0 và đồng biến khi x > 0.
b) Vì -2012 < 0 nên hàm số y = -2012x2 đồng biến khi x < 0 và nghịch biến khi x > 0.
c) Vì 1 <
)x2.
Giải. a) Vì 0,12 > 0 nên hàm số y = 0,12x2 nghịch biến khi x < 0 và đồng biến khi x > 0.
b) Vì -2012 < 0 nên hàm số y = -2012x2 đồng biến khi x < 0 và nghịch biến khi x > 0.
c) Vì 1 < 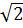 nên 1 -
nên 1 - 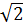 < 0.
Do đó hàm số y = (1 -
< 0.
Do đó hàm số y = (1 - 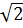 )x2 đồng biến khi x < 0 và nghịch biến khi x > 0.
d) Vì 2 >
)x2 đồng biến khi x < 0 và nghịch biến khi x > 0.
d) Vì 2 > 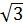 nên 2 -
nên 2 - 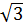 >0.
Do đó hàm số y = (2 -
>0.
Do đó hàm số y = (2 - 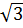 )x2 nghịch biến khi x < 0 và đồng biến khi x > 0.
Ví dụ 5. Tìm giá trị của m để hàm số y = f(x) = (3m - 6)x2 :
a) Đồng biến khi x < 0.
b) f(-7) > f(-
)x2 nghịch biến khi x < 0 và đồng biến khi x > 0.
Ví dụ 5. Tìm giá trị của m để hàm số y = f(x) = (3m - 6)x2 :
a) Đồng biến khi x < 0.
b) f(-7) > f(-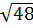 ).
Giải: a) Muốn cho hàm số đồng biến khi x < 0 thì 3m - 6 < 0 hay 3m < 6.
Vậy hàm số y = (3m - 6)x2 đồng biến khi x < 0 nếu m < 2.
b) Vì -7 < -
).
Giải: a) Muốn cho hàm số đồng biến khi x < 0 thì 3m - 6 < 0 hay 3m < 6.
Vậy hàm số y = (3m - 6)x2 đồng biến khi x < 0 nếu m < 2.
b) Vì -7 < -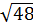 < 0 nên muốn cho f(-7) > f(-
< 0 nên muốn cho f(-7) > f(-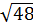 ) thì hàm số phải nghịch biến khi x < 0. Do đó 3m – 6 > 0
Vậy f(-7) > f(-
) thì hàm số phải nghịch biến khi x < 0. Do đó 3m – 6 > 0
Vậy f(-7) > f(-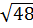 ) khi m > 2.
C. Hướng dẫn giải bài tập trong sách giáo khoa
1. Giải: a)
) khi m > 2.
C. Hướng dẫn giải bài tập trong sách giáo khoa
1. Giải: a)
| R (cm) |
0,57 |
1,37 |
2,15 |
4,09 |
S = 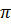 R2 (cm2) R2 (cm2) |
1,02 |
5,89 |
14,51 |
52,53 |
b) Giả sử bán kính của đường tròn đã cho là R. Khi đó diện tích của nó bằng S = 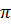 R2
Khi bán kính của nó tăng lên 3 lần ta được một hình tròn mới, với bán kính 3R. Do đó diện tích của hình tròn mới bằng S’ =
R2
Khi bán kính của nó tăng lên 3 lần ta được một hình tròn mới, với bán kính 3R. Do đó diện tích của hình tròn mới bằng S’ = 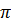 (3R)2 = 9
(3R)2 = 9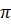 R2 = 9S.
Vậy khi bán kính tăng gấp 3 lần thì diện tích tăng gấp 9 lần.
c) Khi S = 79,5cm2 ; tức là khi
R2 = 9S.
Vậy khi bán kính tăng gấp 3 lần thì diện tích tăng gấp 9 lần.
c) Khi S = 79,5cm2 ; tức là khi 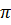 R2 = 79,5cm2 hay 3,14R2
R2 = 79,5cm2 hay 3,14R2 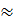 79,5 thì
R2
79,5 thì
R2 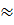 79,5 : 3,14
79,5 : 3,14 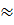 25,32. Do đó R
25,32. Do đó R 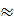
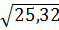
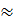 5,03cm.
2. Giải. a) Khoảng cách từ vật rơi đến mặt đất bằng 100m trừ đi quãng đường vật rơi đã đi.
Sau 1 giây vật rơi cách mặt đất 100 - 4.12 =96 (m).
b) Khi vật tiếp đất là lúc quãng đường vật rơi đã đi bằng 100m. Do đó vật tiếp đất khi 4t2 = 100 hay t2 = 100 : 4 = 25 ⇒ t =
5,03cm.
2. Giải. a) Khoảng cách từ vật rơi đến mặt đất bằng 100m trừ đi quãng đường vật rơi đã đi.
Sau 1 giây vật rơi cách mặt đất 100 - 4.12 =96 (m).
b) Khi vật tiếp đất là lúc quãng đường vật rơi đã đi bằng 100m. Do đó vật tiếp đất khi 4t2 = 100 hay t2 = 100 : 4 = 25 ⇒ t = 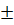 5. Vì thời gian không âm, nên t = 5 (giây).
3. Hướng dẫn. a) Đáp số : a = 30.
b) Trả lời: Khi v = 10m/s thì F = 3000N.
Khi v = 20 m/s thì F = 12 000 N.
c) Giải. Trong gió bão với vận tốc gió 90km/h hay 25m/s, lực tác động lên cánh buồm là F = 30.(25)2 = 18750N.
Nhưng cánh buồm chỉ chịu được một áp lực tối đa là 12 000N nên thuyền này không thể đi được trong bão với tốc độ gió 90km/h.
D. Bài tập luyện thêm
1. Cho hệ trục toạ độ vuông góc, gốc O. Điểm A chạy trên trục hoành, điểm B chạy trên trục tung sao cho
5. Vì thời gian không âm, nên t = 5 (giây).
3. Hướng dẫn. a) Đáp số : a = 30.
b) Trả lời: Khi v = 10m/s thì F = 3000N.
Khi v = 20 m/s thì F = 12 000 N.
c) Giải. Trong gió bão với vận tốc gió 90km/h hay 25m/s, lực tác động lên cánh buồm là F = 30.(25)2 = 18750N.
Nhưng cánh buồm chỉ chịu được một áp lực tối đa là 12 000N nên thuyền này không thể đi được trong bão với tốc độ gió 90km/h.
D. Bài tập luyện thêm
1. Cho hệ trục toạ độ vuông góc, gốc O. Điểm A chạy trên trục hoành, điểm B chạy trên trục tung sao cho 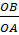 = 2 không đổi. Gọi hoành độ của A là x.
a) Đặt y = AB2, hỏi y có phải là một hàm số của x hay không ? Nếu đúng, hãy viết cống thức của hàm số này.
b) Hãy xác định vị trí của A khi y = 20.
c) Hãy xác định tung độ của B khi A có hoành độ là
= 2 không đổi. Gọi hoành độ của A là x.
a) Đặt y = AB2, hỏi y có phải là một hàm số của x hay không ? Nếu đúng, hãy viết cống thức của hàm số này.
b) Hãy xác định vị trí của A khi y = 20.
c) Hãy xác định tung độ của B khi A có hoành độ là  .
2. Cho hàm số y = (3m + 2)x2. Hãy tìm giá trị của m để :
a) Hàm số đã cho đồng biến khi x > 0.
b) Hàm số đã cho đồng biến khi x < 0.
3. Cho hàm số y = f(x) = ax2. Xác định hệ số a biết rằng f(5) = f(-3) - 8.
4. Cho hàm số y - g(x) = ax2, với g(-7) < g(2). Xét xem hàm số này đồng biến khi nào và nghịch biến khi nào và hệ số a là số âm hay dương ?
Hướng dẫn - Đáp số
1. Giải: a) Khi A có hoành độ là x thì độ dài của đoạn OA bằng | x |.
Vì
.
2. Cho hàm số y = (3m + 2)x2. Hãy tìm giá trị của m để :
a) Hàm số đã cho đồng biến khi x > 0.
b) Hàm số đã cho đồng biến khi x < 0.
3. Cho hàm số y = f(x) = ax2. Xác định hệ số a biết rằng f(5) = f(-3) - 8.
4. Cho hàm số y - g(x) = ax2, với g(-7) < g(2). Xét xem hàm số này đồng biến khi nào và nghịch biến khi nào và hệ số a là số âm hay dương ?
Hướng dẫn - Đáp số
1. Giải: a) Khi A có hoành độ là x thì độ dài của đoạn OA bằng | x |.
Vì 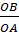 = 2 nên OB = 2| x |.
Theo định lí Py-ta-go, ta có AB2 = OA2 + OB2 = | x |2 + (2 | x |)2 = 5x2.
Vậy y = 5x2 . Đó là một hàm số dạng y = ax2 (a
= 2 nên OB = 2| x |.
Theo định lí Py-ta-go, ta có AB2 = OA2 + OB2 = | x |2 + (2 | x |)2 = 5x2.
Vậy y = 5x2 . Đó là một hàm số dạng y = ax2 (a 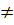 0).
b) Khi y = 20 thì 5x2 = 20. Do đó x2 = 4. Suy ra x = 2 hoặc x = -2.
Vậy A có thể nằm bên phải hoặc bên trái điểm O và cách O là 2 đơn vị.
c) Khi A có hoành độ là
0).
b) Khi y = 20 thì 5x2 = 20. Do đó x2 = 4. Suy ra x = 2 hoặc x = -2.
Vậy A có thể nằm bên phải hoặc bên trái điểm O và cách O là 2 đơn vị.
c) Khi A có hoành độ là  thì OB = 2OA = 1, tức là độ dài của OB bằng 1.
Vậy B có thể nằm phía trên hoặc phía dưới trục hoành và cách o là 1 đơn vị.
Vậy tung độ của B có thể là 1 hoặc -1.
2. Giải. a) Hàm số y = (3m + 2)x2 đồng biến khi x > 0 nếu 3m + 2 > 0 hay m > -
thì OB = 2OA = 1, tức là độ dài của OB bằng 1.
Vậy B có thể nằm phía trên hoặc phía dưới trục hoành và cách o là 1 đơn vị.
Vậy tung độ của B có thể là 1 hoặc -1.
2. Giải. a) Hàm số y = (3m + 2)x2 đồng biến khi x > 0 nếu 3m + 2 > 0 hay m > -  .
b) Hàm số y = (3m + 2)x2 đồng biến khi x < 0 nếu m < -
.
b) Hàm số y = (3m + 2)x2 đồng biến khi x < 0 nếu m < -  .
3. Giải. Ta có f(5) = 25a, f(-3) = 9a. Theo đầu bài, ta có : 25a = 9a - 8.
Do đó 16a = -8.
Vậy a =
.
3. Giải. Ta có f(5) = 25a, f(-3) = 9a. Theo đầu bài, ta có : 25a = 9a - 8.
Do đó 16a = -8.
Vậy a = 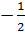 .
4. Giải. Vì g(-7) = g(7) nên g(7) < g(2). Điều này chứng tỏ hàm số nghịch biến khi x > 0 và do đó đồng biến khi x < 0. Vậy a < 0.
.
4. Giải. Vì g(-7) = g(7) nên g(7) < g(2). Điều này chứng tỏ hàm số nghịch biến khi x > 0 và do đó đồng biến khi x < 0. Vậy a < 0.
© Bản quyền thuộc về
Bài kiểm tra. Ghi rõ nguồn Bài kiểm tra.com khi sao chép nội dung này.