Giải bài tập Toán 9, chương IV, bài 3: Phương trình bậc hai một ẩn.
2019-08-23T22:23:59-04:00
2019-08-23T22:23:59-04:00
Giải bài tập Toán 9, chương IV, bài 3: Phương trình bậc hai một ẩn: Tóm tắt kiến thức, ví dụ, hướng dẫn giải bài tập trong sách giáo khoa và bài tập luyện thêm.
/themes/cafe/images/no_image.gif
Bài Kiểm Tra
https://baikiemtra.com/uploads/bai-kiem-tra-logo.png
Thứ sáu - 23/08/2019 22:22
Giải bài tập Toán 9, chương IV, bài 3: Phương trình bậc hai một ẩn: Tóm tắt kiến thức, ví dụ, hướng dẫn giải bài tập trong sách giáo khoa và bài tập luyện thêm.
A. Tóm tắt kiến thức
1. Định nghĩa
Phương trình bậc hai một ẩn (nói gọn là phương trình bậc hai) là phương trình có dạng: ax2 + bx + c = 0, trong đó x là ẩn ; a, b, c là những số cho trước gọi là các hệ số và a 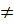 0.
2. Cách giải một vài dạng phương trình bậc hai
a) Dạng ax2 + bx = 0 (c = 0)
Đưa về phương trình tích : x(ax + b) = 0.
Phương trình có nghiệm là : x1 = 0 và x2 =
0.
2. Cách giải một vài dạng phương trình bậc hai
a) Dạng ax2 + bx = 0 (c = 0)
Đưa về phương trình tích : x(ax + b) = 0.
Phương trình có nghiệm là : x1 = 0 và x2 = 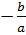 b) Dạng ax2 + c = 0 (b = 0)
Đưa về phương trình : x2 =
b) Dạng ax2 + c = 0 (b = 0)
Đưa về phương trình : x2 = 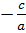 .
Nếu
.
Nếu  > 0 thì phương trình vô nghiệm,
Nếu
> 0 thì phương trình vô nghiệm,
Nếu 
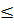 0 thì phương trình có nghiệm x =
0 thì phương trình có nghiệm x = 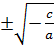 c) Dạng ax2 + bx + c = 0, với a, b, c khác 0.
Đưa phương trình về dạng vế trái là một bình phương, vế phải là một hằng số.
Biến đổi vế trái :
ax2 + bx = -c ⇔ x2 +
c) Dạng ax2 + bx + c = 0, với a, b, c khác 0.
Đưa phương trình về dạng vế trái là một bình phương, vế phải là một hằng số.
Biến đổi vế trái :
ax2 + bx = -c ⇔ x2 +  x = -
x = -  ⇔ x2.
⇔ x2. 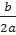 x +
x + 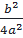 =
= 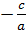 +
+ 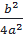 ⇔
⇔ 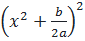 =
= 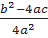 B. Ví dụ
Ví dụ 1: Những phương trình nào sau đây là phương trình bậc hai. Hãy xác định các hệ số a, b, c của những phương trình bậc hai đó:
B. Ví dụ
Ví dụ 1: Những phương trình nào sau đây là phương trình bậc hai. Hãy xác định các hệ số a, b, c của những phương trình bậc hai đó:
| a) 4x2 + 9x + 2 = 0 |
b) - 3x2 + 5x = 0 |
| c) 6x + 7 = 0 |
d) x2 – 9 = 0 |
| e) x3 - 2x + 1 = 0 |
f) -8x2 = 0 |
Giải: a) 4x2 + 9x + 2 = 0 là một phương trình bậc hai với a = 4, b = 9, c = 2
b) -3x2 + 5x = 0 là một phương trình bậc hai với a = -3, b = 5, c = 0.
c) 6x + 7 = 0 không phải là một phương trình bậc hai.
d) x2 - 9 = 0 là một phương trình bậc hai với a = 1, b = 0, c = -9.
e) x3 - 2x + 1 = 0 không phải là một phương trình bậc hai.
f) -8x2 = 0 là một phương trình bậc hai với a = - 8, b = 0, c = 0.
Ví dụ 2. Giải phương trình :
a) 2x2 - 6x = 0 ; b) 5x2 + 8x = 0.
Giải. a) 2x2 - 6x = 0 ⇔ 2x(x - 3) = 0 ⇔ x = 0 hoặc x - 3 = 0
⇔ x = 0 hoặc x = 3.
Phương trình có hai nghiệm là x1 = 0, x2 = 3.
b) 5x2 + 8x = 0 ⇔ x(5x + 8) = 0 ⇔ x = 0 hoặc 5x + 8 = 0
⇔ x = 0 hoặc 5x = -8 ⇔ x = 0 hoặc x = - 4.
Phương trình có hai nghiệm là : x1 = 0, x2 = 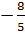 .
Ví dụ 3. Giải phương trình :
a) -5x2 + 10 = 0;
b) 2x2 + 4 = 0.
Giải: a) -5x2 + 10 = 0 ⇔ 5x2 = 10 ⇔ x2 = 2 ⇔ x =
.
Ví dụ 3. Giải phương trình :
a) -5x2 + 10 = 0;
b) 2x2 + 4 = 0.
Giải: a) -5x2 + 10 = 0 ⇔ 5x2 = 10 ⇔ x2 = 2 ⇔ x = 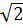 hoặc x = -
hoặc x = - 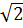 .
Phương trình có hai nghiệm : x1 =
.
Phương trình có hai nghiệm : x1 = 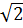 , x2 = -
, x2 = - 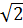 .
b) 2x2 + 4 = 0 ⇔ 2x2 = - 4. Vì vế trái không âm còn vế phải âm nên không có giá trị nào thoả mãn phương trình này. Phương trình vô nghiệm.
Ví dụ 4. Giải phương trình :
a) 2x2 - 5x + 2 = 0 ;
b) 2x2 + 4x + 3 = 0.
Giải. a) 2x2 - 5x + 2 = 0 ⇔ 2x2 - 5x = -2 ⇔ x2 - 52
.
b) 2x2 + 4 = 0 ⇔ 2x2 = - 4. Vì vế trái không âm còn vế phải âm nên không có giá trị nào thoả mãn phương trình này. Phương trình vô nghiệm.
Ví dụ 4. Giải phương trình :
a) 2x2 - 5x + 2 = 0 ;
b) 2x2 + 4x + 3 = 0.
Giải. a) 2x2 - 5x + 2 = 0 ⇔ 2x2 - 5x = -2 ⇔ x2 - 52 x = - 1
⇔ x2 – 2.
x = - 1
⇔ x2 – 2.  x +
x + 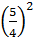 = -1 +
= -1 + 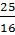 ⇔
⇔ 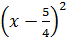 =
= 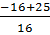 ⇔
⇔ 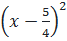 =
= 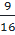 ⇔ x -
⇔ x -  =
= 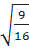 hoặc x -
hoặc x -  =
= 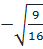 ⇔ x -
⇔ x -  =
=  hoặc x -
hoặc x -  =
= 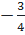 ⇔ x =2 hoặc x =
⇔ x =2 hoặc x =  Phương trình có hai nghiệm phân biệt: x1=2; x2 =
Phương trình có hai nghiệm phân biệt: x1=2; x2 =  b) 2x2 + 4x + 3 = 0 ⇔ 2x2 + 4x = - 3 ⇔ x2 + 2x =
b) 2x2 + 4x + 3 = 0 ⇔ 2x2 + 4x = - 3 ⇔ x2 + 2x = 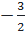 ⇔ x2 + 2x + 1=
⇔ x2 + 2x + 1= 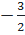 + 1 ⇔ (x+1)2 =
+ 1 ⇔ (x+1)2 = 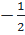 Vì vế trái không âm, vế phải âm nên phương trình vô nghiệm.
C. Hướng dẫn giải bài tập trong sách giáo khoa
11. Trả lời :
a) 5x2 + 3x - 4 = 0, với a = 5, b = 3, c = - 4.
b)
Vì vế trái không âm, vế phải âm nên phương trình vô nghiệm.
C. Hướng dẫn giải bài tập trong sách giáo khoa
11. Trả lời :
a) 5x2 + 3x - 4 = 0, với a = 5, b = 3, c = - 4.
b)  x2 - x -
x2 - x - 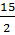 = 0, với a =
= 0, với a =  ; b = -1; c =
; b = -1; c = 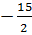 c) 2x2 + (1 -
c) 2x2 + (1 - 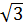 )x - (1 +
)x - (1 + 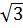 ) = 0, với a = 2; b =1 -
) = 0, với a = 2; b =1 - 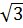 ; c = - (1 +
; c = - (1 + 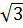 )
d) 2x2 - 2(m - 1)x + m2 = 0, với a = 2, b = - 2(m - 1), c = m2.
12. Đáp số:
a) x =
)
d) 2x2 - 2(m - 1)x + m2 = 0, với a = 2, b = - 2(m - 1), c = m2.
12. Đáp số:
a) x = 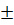 2
2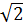 ; b) x =
; b) x = 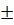 2 ;
c) Vô nghiệm ; d) x1 = 0; x2 =
2 ;
c) Vô nghiệm ; d) x1 = 0; x2 = 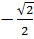 ; e) x1 = 0; x2 = 3
13. Giải: a) x2 + 8x = -2 ⇔ x2 + 8x + 16 = -2 + 16 ⇔ (x + 4)2 = 14.
b) x2 + 2x =
; e) x1 = 0; x2 = 3
13. Giải: a) x2 + 8x = -2 ⇔ x2 + 8x + 16 = -2 + 16 ⇔ (x + 4)2 = 14.
b) x2 + 2x =  ⇔x2 + 2x + 1 =
⇔x2 + 2x + 1 =  + 1 ⇔ (x + 1)2 =
+ 1 ⇔ (x + 1)2 =  .
14. Giải. 2x2 + 5x + 2 = 0 ⇔ 2x2 + 5x = -2 ⇔ x2 +
.
14. Giải. 2x2 + 5x + 2 = 0 ⇔ 2x2 + 5x = -2 ⇔ x2 +  x = -1
⇔ x2 + 2.
x = -1
⇔ x2 + 2. x +
x + 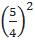 = -1 +
= -1 + 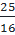 ⇔
⇔ 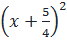 =
= 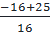 ⇔
⇔ 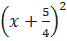 =
= 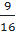 ⇔
⇔ 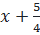 =
= 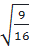 hoặc
hoặc 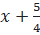 =
= 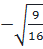 ⇔
⇔ 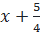 =
=  hoặc
hoặc 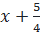 =
= 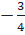 ⇔ x =
⇔ x = 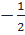 hoặc x = -2
Phương trình có hai nghiệm phân biệt: x1 =
hoặc x = -2
Phương trình có hai nghiệm phân biệt: x1 = 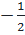 , x2 = -2.
D. Bài tập luyện thêm
1. Giải phương trình :
a) 3x2 + 9x = 0 b) 4x2 - 12x = 0 ;
c) 5x2 - 7 = 0 d) 12x2+ 1 =0.
2. Giải phương trình bằng cách đưa về phương trình có vế trái là một bình phương và vế phải là một hằng số :
a) x2 + 6x - 7 = 0 ; b) 2x2 - 4x - 3 = 0 ; c) 3x2 + 6x + 4 = 0
3. Cho phương trình (m - 1 )x2 - 2(2m + 1 )x + 3m + 3 = 0.
a) Tìm các giá trị của m để phương trình đã cho là một phương trình bậc hai.
b) Giải phương trình khi m = 2 bằng cách đưa phương trình về dạng vế trái là một bình phương và vế phải là một hằng số.
c) Chứng tỏ rằng phương trình luôn có nghiệm x = 1.
Hướng dẫn - Đáp số
1. Đáp số: a) x1 = 0, x2 = - 3 ; b) x1 = 0, x2 = 3
c) x1 =
, x2 = -2.
D. Bài tập luyện thêm
1. Giải phương trình :
a) 3x2 + 9x = 0 b) 4x2 - 12x = 0 ;
c) 5x2 - 7 = 0 d) 12x2+ 1 =0.
2. Giải phương trình bằng cách đưa về phương trình có vế trái là một bình phương và vế phải là một hằng số :
a) x2 + 6x - 7 = 0 ; b) 2x2 - 4x - 3 = 0 ; c) 3x2 + 6x + 4 = 0
3. Cho phương trình (m - 1 )x2 - 2(2m + 1 )x + 3m + 3 = 0.
a) Tìm các giá trị của m để phương trình đã cho là một phương trình bậc hai.
b) Giải phương trình khi m = 2 bằng cách đưa phương trình về dạng vế trái là một bình phương và vế phải là một hằng số.
c) Chứng tỏ rằng phương trình luôn có nghiệm x = 1.
Hướng dẫn - Đáp số
1. Đáp số: a) x1 = 0, x2 = - 3 ; b) x1 = 0, x2 = 3
c) x1 = 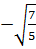 ;x2 =
;x2 = 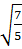 d) Vô nghiệm.
2. Giải: a) x2 + 6x - 7 = 0 ⇔ x2 + 6x = 7 ⇔ x2 + 2.3x + 9 = 7 + 9
⇔ (x + 3)2 = 16 ⇔ x + 3 = 4 hoặc x + 3 = - 4 ⇔ x = 1 hoặc x = -7.
b) 2x2 - 4x - 3 = 0 ⇔ 2x2 - 4x = 3 ⇔ x2 - 2x =
d) Vô nghiệm.
2. Giải: a) x2 + 6x - 7 = 0 ⇔ x2 + 6x = 7 ⇔ x2 + 2.3x + 9 = 7 + 9
⇔ (x + 3)2 = 16 ⇔ x + 3 = 4 hoặc x + 3 = - 4 ⇔ x = 1 hoặc x = -7.
b) 2x2 - 4x - 3 = 0 ⇔ 2x2 - 4x = 3 ⇔ x2 - 2x =  ⇔ x2 - 2x =
⇔ x2 - 2x =  + 1 ⇔ (x - 1)2 =
+ 1 ⇔ (x - 1)2 =  ⇔ x -1 =
⇔ x -1 = 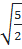 hoặc x -1 =
hoặc x -1 = 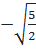 ⇔ x =1 +
⇔ x =1 +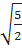 hoặc x = 1
hoặc x = 1 -
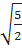 hay x =
hay x = 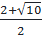 hoặc x =
hoặc x = 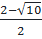 c) 3x2 + 6x + 4 = 0 ⇔ 3x2 + 6x = -4 ⇔ x2 + 2x =
c) 3x2 + 6x + 4 = 0 ⇔ 3x2 + 6x = -4 ⇔ x2 + 2x = 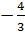 ⇔ x2 + 2x + 1 =
⇔ x2 + 2x + 1 = 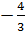 + 1 ⇔ (x + 1)2 =
+ 1 ⇔ (x + 1)2 = 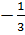 Phương trình vô nghiệm.
3. Giải: a) Phương trình đã cho là một phương trình bậc hai khi m - 1
Phương trình vô nghiệm.
3. Giải: a) Phương trình đã cho là một phương trình bậc hai khi m - 1 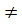 0 hay khi m
0 hay khi m 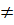 1,
b) Khi m = 2, phương trình đã cho trở thành : x2 - 10x + 9 = 0.
Ta có : x2 - 10x + 9 = 0 ⇔ x2 - 10x = -9 ⇔ x2 - 2. x. 5 + 52 = -9 + 52
⇔ (x - 5)2 = 16 ⇔ x - 5 = 4 hoặc x – 5 = - 4 ⇔x = 9 hoặc x = 1.
Với x = 1, ta có:
(m - 1).12 - 2(2m + 1).1 + 3m + 3 = m - 1 - 4m - 2 + 3m + 3 = 0.
Vậy với mọi giá trị của m thì x = 1 luôn là nghiệm của phương trình đã cho.
1,
b) Khi m = 2, phương trình đã cho trở thành : x2 - 10x + 9 = 0.
Ta có : x2 - 10x + 9 = 0 ⇔ x2 - 10x = -9 ⇔ x2 - 2. x. 5 + 52 = -9 + 52
⇔ (x - 5)2 = 16 ⇔ x - 5 = 4 hoặc x – 5 = - 4 ⇔x = 9 hoặc x = 1.
Với x = 1, ta có:
(m - 1).12 - 2(2m + 1).1 + 3m + 3 = m - 1 - 4m - 2 + 3m + 3 = 0.
Vậy với mọi giá trị của m thì x = 1 luôn là nghiệm của phương trình đã cho.
© Bản quyền thuộc về
Bài kiểm tra. Ghi rõ nguồn Bài kiểm tra.com khi sao chép nội dung này.