Giải bài tập Toán 9, chương IV, bài 4: Công thức nghiệm của phương trình bậc hai.
2019-08-23T23:57:45-04:00
2019-08-23T23:57:45-04:00
Giải bài tập Toán 9, chương IV, bài 4: Công thức nghiệm của phương trình bậc hai: Tóm tắt kiến thức, ví dụ, hướng dẫn giải bài tập trong sách giáo khoa và bài tập luyện thêm.
/themes/cafe/images/no_image.gif
Bài Kiểm Tra
https://baikiemtra.com/uploads/bai-kiem-tra-logo.png
Thứ sáu - 23/08/2019 23:57
Giải bài tập Toán 9, chương IV, bài 4: Công thức nghiệm của phương trình bậc hai: Tóm tắt kiến thức, ví dụ, hướng dẫn giải bài tập trong sách giáo khoa và bài tập luyện thêm.
A. Tóm tắt kiến thức
Đối với phương trình bậc hai ax + bx + c = 0, ta gọi biểu thức b2 - 4ac là biệt thức của nó và kí hiệu là  ; tức là
; tức là  = b2 - 4ac.
- Nếu
= b2 - 4ac.
- Nếu  > 0 thì phương trình có hai nghiệm phân biệt:
x1 =
> 0 thì phương trình có hai nghiệm phân biệt:
x1 = 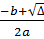 ; x2 =
; x2 = 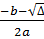 - Nếu
- Nếu  = 0 thì phương trình có nghiệm kép:
x1 = x2 =
= 0 thì phương trình có nghiệm kép:
x1 = x2 = 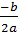 - Nếu
- Nếu  < 0 thì phương trình vô nghiệm:
Lưu ý. a) Nêu phương trình ax2 + bx + c = 0 có a và c trái dấu, tức là ac < 0 thì
< 0 thì phương trình vô nghiệm:
Lưu ý. a) Nêu phương trình ax2 + bx + c = 0 có a và c trái dấu, tức là ac < 0 thì
 = b2 - 4ac > 0. Do đó phương trình có hai nghiệm phân biệt.
b) Đối với các phương trình bậc hai dạng ax2 + bx = 0 hoặc ax2 + c = 0, ta vẫn có thể dùng biệt thức
= b2 - 4ac > 0. Do đó phương trình có hai nghiệm phân biệt.
b) Đối với các phương trình bậc hai dạng ax2 + bx = 0 hoặc ax2 + c = 0, ta vẫn có thể dùng biệt thức  để giải. Tuy nhiên, cách giải đã nêu trong bài trước thuận tiện hơn.
B. Ví dụ
Ví dụ 1. Xác định các hệ số, tính biệt thức
để giải. Tuy nhiên, cách giải đã nêu trong bài trước thuận tiện hơn.
B. Ví dụ
Ví dụ 1. Xác định các hệ số, tính biệt thức  của các phương trình sau, rồi cho biết mỗi phương trình đó có nghiệm hay không :
a) 5x2 - 8x + 2 = 0 ; b) -2x2 + 3x + 5 = 0 ; c) 2x2 - x + 1 = 0 ;
d) 6x2 + 5 = 0; e) 7x2 + 3x = 0.
Giải: a) Phương trình có các hệ số là : a = 5, b = -8, c = 2.
của các phương trình sau, rồi cho biết mỗi phương trình đó có nghiệm hay không :
a) 5x2 - 8x + 2 = 0 ; b) -2x2 + 3x + 5 = 0 ; c) 2x2 - x + 1 = 0 ;
d) 6x2 + 5 = 0; e) 7x2 + 3x = 0.
Giải: a) Phương trình có các hệ số là : a = 5, b = -8, c = 2.
 = (-8)2 - 4.5.2 = 64 - 40 = 24 > 0.
Phương trình có hai nghiệm phân biệt.
b) Phương trình có các hệ số là : a = -2, b = 3, c = 5.
= (-8)2 - 4.5.2 = 64 - 40 = 24 > 0.
Phương trình có hai nghiệm phân biệt.
b) Phương trình có các hệ số là : a = -2, b = 3, c = 5.
 = 32 - 4.(-2).5 = 9 + 40 = 49 > 0.
Phương trình có hai nghiệm phân biệt.
Lưu ý. Ta có thể khẳng định ngay rằng phương trình -2x2 + 3x + 5 = 0 có hai nghiệm phân biệt vì a = -2 và c = 5 trái dấu.
c) Phương trình có các hệ số là : a = 2, b = -1, c = 1.
= 32 - 4.(-2).5 = 9 + 40 = 49 > 0.
Phương trình có hai nghiệm phân biệt.
Lưu ý. Ta có thể khẳng định ngay rằng phương trình -2x2 + 3x + 5 = 0 có hai nghiệm phân biệt vì a = -2 và c = 5 trái dấu.
c) Phương trình có các hệ số là : a = 2, b = -1, c = 1.
 = (-1)2 - 4.2.1 = 1 - 8 = -7 <0.
Phương trình vô nghiệm.
d) Phương trình có các hệ số là : a = 6, b = 0, c = 5.
= (-1)2 - 4.2.1 = 1 - 8 = -7 <0.
Phương trình vô nghiệm.
d) Phương trình có các hệ số là : a = 6, b = 0, c = 5.
 = 02 - 4.6.5 = - 120 < 0.
Phương trình vô nghiệm.
e) Phương trình có các hệ số là : a = 7, b = 3, c = 0.
= 02 - 4.6.5 = - 120 < 0.
Phương trình vô nghiệm.
e) Phương trình có các hệ số là : a = 7, b = 3, c = 0.
 = 32 - 4.7.0 = 9 > 0.
Phương trình có hai nghiệm phân biệt.
Ví dụ 2. Dùng công thức nghiệm, giải các phương trình sau :
a) x2 - 8x + 15 = 0 ; b) 2x2 + 5x - 3 = 0 ;
c) 36x2 - 12x+1 = 0; d) 5x2 + 2x + 1 = 0.
Giải: a)
= 32 - 4.7.0 = 9 > 0.
Phương trình có hai nghiệm phân biệt.
Ví dụ 2. Dùng công thức nghiệm, giải các phương trình sau :
a) x2 - 8x + 15 = 0 ; b) 2x2 + 5x - 3 = 0 ;
c) 36x2 - 12x+1 = 0; d) 5x2 + 2x + 1 = 0.
Giải: a)  = (-8)2 - 4.1.15 = 64 - 60 = 4.
= (-8)2 - 4.1.15 = 64 - 60 = 4.
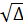 =
= 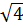 = 2.
Phương trình có hai nghiệm phân biệt:
x1 =
= 2.
Phương trình có hai nghiệm phân biệt:
x1 = 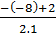 = 5 ; x2 =
= 5 ; x2 = 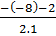 = 3
b)
= 3
b)  = 52 - 4.2.(-3) = 49.
= 52 - 4.2.(-3) = 49.
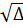 =
= 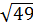 = 7.
Phương trình có hai nghiệm phân biệt:
x1 =
= 7.
Phương trình có hai nghiệm phân biệt:
x1 = 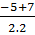 =
=  ; x2 =
; x2 = 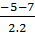 = -3
c)
= -3
c)  = (12)2 - 4.36.1 = 144 - 144 = 0.
Phương trình có nghiệm kép : x1 = x2 =
= (12)2 - 4.36.1 = 144 - 144 = 0.
Phương trình có nghiệm kép : x1 = x2 = 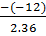 =
=  d)
d)  = 22 - 4.5.1 = 4 - 20 = -16 < 0.
Phương trình vô nghiệm.
C. Hướng dẫn giải bài tập trong sách giáo khoa
15. Giải.
a) a = 7, b = - 2, c = 3.
= 22 - 4.5.1 = 4 - 20 = -16 < 0.
Phương trình vô nghiệm.
C. Hướng dẫn giải bài tập trong sách giáo khoa
15. Giải.
a) a = 7, b = - 2, c = 3.
 = (-2)2 - 4.7.3 = 4 - 84 = -80 < 0.
Phương trình vô nghiệm.
b) a = 5, b = 2
= (-2)2 - 4.7.3 = 4 - 84 = -80 < 0.
Phương trình vô nghiệm.
b) a = 5, b = 2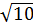 , c = 2.
, c = 2.
 = (2
= (2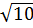 )2 - 4.5.2 = 40 - 40 = 0.
Phương trình có nghiệm kép.
c) a =
)2 - 4.5.2 = 40 - 40 = 0.
Phương trình có nghiệm kép.
c) a =  , b = 7, c =
, b = 7, c = 
 =
= 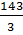 > 0
Phương trình có hai nghiệm phân biệt.
d) a = 1,7, b = -1,2, c = - 2,1.
> 0
Phương trình có hai nghiệm phân biệt.
d) a = 1,7, b = -1,2, c = - 2,1.
 = 15,72 > 0.
Phương trình có hai nghiệm phân biệt.
16. Giải.
a)
= 15,72 > 0.
Phương trình có hai nghiệm phân biệt.
16. Giải.
a)  = (-7) - 4.2.3 = 49 - 24 = 25.
= (-7) - 4.2.3 = 49 - 24 = 25.
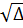 = 5. Phương trình có hai nghiệm phân biệt:
x1 =
= 5. Phương trình có hai nghiệm phân biệt:
x1 = 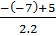 = 3 , x2 =
= 3 , x2 = 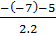 =
=  b) Trả lời : Vô nghiệm ;
c) Trả lời : x1 =
b) Trả lời : Vô nghiệm ;
c) Trả lời : x1 =  , x2 = -1.
d) Trả lời : x1 =
, x2 = -1.
d) Trả lời : x1 = 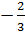 , x2 = -1.
e) Giải.
, x2 = -1.
e) Giải.  = (-8)2 - 4.1.16 = 64 - 64 = 0.
Phương trình có nghiệm kép :
x1 = x2 =
= (-8)2 - 4.1.16 = 64 - 64 = 0.
Phương trình có nghiệm kép :
x1 = x2 = 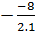 = 4
f) Trả lời: Phương trình có nghiệm kép : x1 = x2 =
= 4
f) Trả lời: Phương trình có nghiệm kép : x1 = x2 = 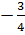 D. Bài tập luyện thêm
1. Giải các phương trình :
a) x2 -
D. Bài tập luyện thêm
1. Giải các phương trình :
a) x2 -  x -
x -  = 0; b)
= 0; b)  x2 + 7x +
x2 + 7x +  = 0 c) 6x2 + 0,8x + 0,02 = 0.
2. Giải các phương trình :
a) 2
= 0 c) 6x2 + 0,8x + 0,02 = 0.
2. Giải các phương trình :
a) 2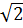 x2 - 5
x2 - 5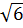 x + 9
x + 9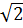 = 0
b) 7x2 - 3
= 0
b) 7x2 - 3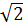 x -1 = 3x2 +
x -1 = 3x2 + 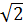 x
3. Cho phương trình (m - 2)x2 + (2m - 1)x + m + 2 = 0. Tìm giá trị của m để phương trình :
a) Có hai nghiệm phân biệt.
b) Có nghiệm kép.
c) Vô nghiệm.
Hướng dẫn - Đáp số
1. Đáp số: a) x1 = 2, x2 =
x
3. Cho phương trình (m - 2)x2 + (2m - 1)x + m + 2 = 0. Tìm giá trị của m để phương trình :
a) Có hai nghiệm phân biệt.
b) Có nghiệm kép.
c) Vô nghiệm.
Hướng dẫn - Đáp số
1. Đáp số: a) x1 = 2, x2 = 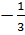 ;
b) x1 =
;
b) x1 = 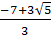 ; x2 =
; x2 = 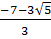 c) x1 =
c) x1 = 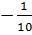 ; x2 =
; x2 = 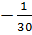 2. Giải. a)
2. Giải. a)  = (-5
= (-5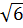 )2 - 4.2
)2 - 4.2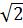 .9
.9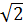 = 150 - 144 = 6.
= 150 - 144 = 6.
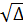 =
= 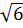 x1 =
x1 = 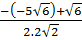 =
= 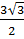 ; x2 =
; x2 = 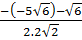 =
= 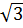 b) 7x2 -3
b) 7x2 -3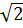 x - 1 = 3x2 +
x - 1 = 3x2 + 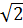 x ⇔ 4x2 - 4
x ⇔ 4x2 - 4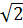 x - 1 = 0.
x - 1 = 0.
 = (- 4
= (- 4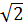 )2 - 4.4.(-1) = 32 + 16 = 48.
)2 - 4.4.(-1) = 32 + 16 = 48.
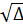 =
= 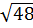 = 4
= 4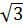 .
x1 =
.
x1 = 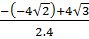 =
= 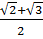 ; x2 =
; x2 = 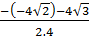 =
= 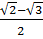 3. Phân tích. Muốn cho một phương trình ax2 + bx + c = 0 có hai nghiệm phân biệt hoặc có nghiệm kép thì trước hết a
3. Phân tích. Muốn cho một phương trình ax2 + bx + c = 0 có hai nghiệm phân biệt hoặc có nghiệm kép thì trước hết a 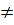 0. Sau đó ta cần xét
0. Sau đó ta cần xét  Giải. Trước hết m - 2
Giải. Trước hết m - 2 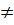 0 hay m
0 hay m 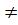 2.
2.
 = (2m - 1)2 - 4(m - 2)(m + 2) = 4m2 - 4m + 1 - 4m2 + 16 = - 4m + 17.
Phương trình có hai nghiệm phân biệt khi - 4m + 17 > 0 hay khi m <
= (2m - 1)2 - 4(m - 2)(m + 2) = 4m2 - 4m + 1 - 4m2 + 16 = - 4m + 17.
Phương trình có hai nghiệm phân biệt khi - 4m + 17 > 0 hay khi m < 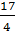 và m
và m 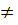 2.
Phương trình có nghiệm kép khi - 4m +17 = 0 hay khi m =
2.
Phương trình có nghiệm kép khi - 4m +17 = 0 hay khi m = 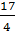 Phương trình vô nghiệm khi - 4m + 17 < 0 hay khi m >
Phương trình vô nghiệm khi - 4m + 17 < 0 hay khi m > 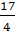
© Bản quyền thuộc về
Bài kiểm tra. Ghi rõ nguồn Bài kiểm tra.com khi sao chép nội dung này.