Giải bài tập Hình học 9, chương I: Bài 4: Một số hệ thức về cạnh và góc trong tam giác vuông.
2019-08-02T21:49:03-04:00
2019-08-02T21:49:03-04:00
Giải bài tập Hình học 9, chương I: Bài 4: Một số hệ thức về cạnh và góc trong tam giác vuông.
/themes/cafe/images/no_image.gif
Bài Kiểm Tra
https://baikiemtra.com/uploads/bai-kiem-tra-logo.png
Thứ sáu - 02/08/2019 21:47
Giải bài tập Hình học 9, chương I: Bài 4: Một số hệ thức về cạnh và góc trong tam giác vuông.
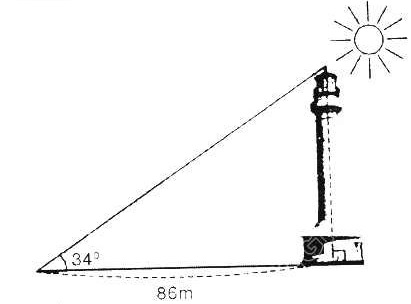
| Bài 1. Các tia nắng mặt trời tạo với mặt đất một góc xấp xỉ bằng 34o và bóng mát của một tháp trên mặt đất dài 86m. Tính chiều cao của tháp (làm tròn đến mét). |
|
Giải:
Từ đỉnh tháp ta vẽ một đường thẳng vuông góc với mặt đất, khoảng cách từ đỉnh đến mặt đất được gọi là chiều cao tháp và khoảng cách từ chân đường cao đến giao điểm các tia nắng mặt trời tạo với mặt đất chính là bóng của tháp trên mặt đất.
Khi đó, ta có chiều cao của tháp bằng: 86.tg34o 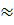 58 (m)
Đáp số: 58 mét.
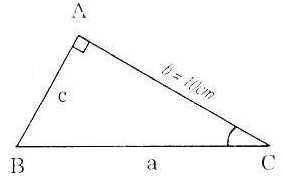
Bài 2. Giải tam giác ABC vuông tại A, biết rằng:
a) b = 10cm,
58 (m)
Đáp số: 58 mét.
Bài 2. Giải tam giác ABC vuông tại A, biết rằng:
a) b = 10cm, 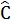 = 30°; b) c = 10cm,
= 30°; b) c = 10cm, 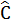 = 45°;
c) a = 20cm,
= 45°;
c) a = 20cm, 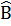 = 35°; d) c = 21cm, b = 18cm.
Giải:
= 35°; d) c = 21cm, b = 18cm.
Giải:
a) Ta có: 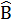 = 90o - = 90o - 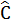 = 90o – 30o = 60o = 90o – 30o = 60o
c = b.tg30o = 10.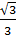 = = 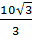 (cm) (cm)
a2 = b2 + c2 = 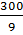 + 100 + 100
= 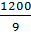 ⇒ a = ⇒ a = 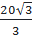 (cm) (cm) |
|
b) B = 45o
b = 10cm
a = 10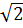 cm cm |
c) C = 55o
b = 11,5cm
c = 16,4cm |
d) 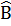 = 40o36’ = 40o36’
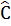 = 49o24’ = 49o24’
a = 27,7cm |
BÀI TẬP LÀM THÊM
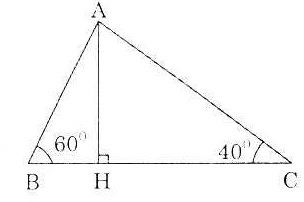
Bài 1. Cho tam giác ABC có BC = 9cm. 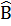 = 60o, = 60o, 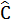 = 40o. Dùng bảng lượng giác tính các cạnh AB, AC (Làm tròn kết quả đến chữ số thập phân thứ nhất). = 40o. Dùng bảng lượng giác tính các cạnh AB, AC (Làm tròn kết quả đến chữ số thập phân thứ nhất). |
 |
Giải:
Cách 1:
Ta có: BH = AH.cotg60o, CH = AH. cotg40o
Suy ra: BH + CH = AH (cotg60o + cotg40o)
⇒ BC = AH(cotg60o + cotg40o)
⇒ AH = 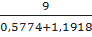 =
= 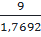
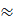 5,1(cm)
AB =
5,1(cm)
AB = 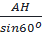 =
= 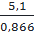
 5,9(cm)
AC =
5,9(cm)
AC = 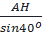 =
= 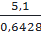
 7,9(cm)
Cách 2:
Ta tính được
7,9(cm)
Cách 2:
Ta tính được 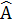 = 80o. Áp dụng công thức:
a
= 80o. Áp dụng công thức:
a 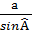 = b
= b 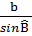 = c
= c 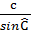 Ta có:
Ta có: 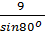 =
=  =
=  Do đó: AB =
Do đó: AB = 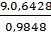
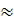 5,9 (cm)
AC =
5,9 (cm)
AC = 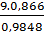
 7,9 (cm)
7,9 (cm)
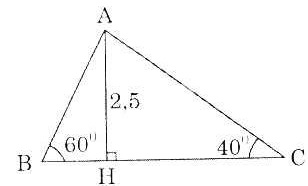
Bài 2. Cho tam giác ABC có 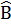 = 60°, = 60°, 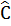 = 40o. Đường cao AH = 2,5cm. Dùng bảng lượng giác tính các cạnh của tam giác ABC. = 40o. Đường cao AH = 2,5cm. Dùng bảng lượng giác tính các cạnh của tam giác ABC. |
 |
Giải:
Ta có: AH = AB.sin60o
⇒ AB = 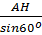
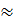
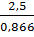 ⇒ AB
⇒ AB 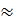 2,9 (cm)
Tương tự: AC =
2,9 (cm)
Tương tự: AC = 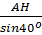
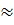
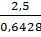 ⇒ AC
⇒ AC 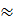 3,9 (cm)
BC = BH + HC = AH(cotg60° + cotg40o )
3,9 (cm)
BC = BH + HC = AH(cotg60° + cotg40o )
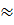 2,5(0,5774 + 1,1918)
2,5(0,5774 + 1,1918) 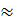 4,4 (cm)
4,4 (cm)
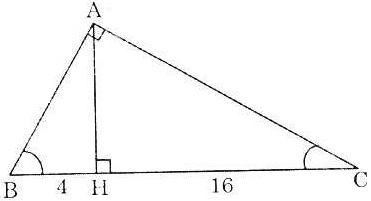
Bài 3. Cho tam giác ABC vuông tại A, đường cao AH. Cho biết BH = 4cm; HC = 16cm. Hãy tính:
a) Tính 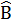 và và 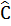 . .
b) Diện tích  ABC. ABC. |
 |
Giải:
a) Tính B và C :
Từ tam giác ABC vuông tại A, ta có:
AH2 = HB.HC = 4.16 = 64 ⇒ AH = 8 (cm)
Từ  AHB vuông tại H, ta có:
tg
AHB vuông tại H, ta có:
tg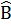 =
= 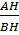 =
=  = 2 ⇒
= 2 ⇒ 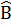
 63o
Từ
63o
Từ  AHC vuông tại H, ta có: tg
AHC vuông tại H, ta có: tg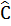 =
= 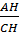 =
= 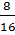 =
=  ⇒
⇒ 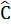 = 27o (Có thể tính
= 27o (Có thể tính 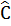 = 90o -
= 90o - 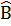 = 27o)
b)
= 27o)
b) 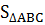 =
=  AH.BC =
AH.BC =  .8.20 = 80 (cm2)
Vậy
.8.20 = 80 (cm2)
Vậy 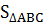 = 80cm2.
= 80cm2.
Bài 4. Cho hình thang cân ABCD (AB // CD), đường cao AH. Cho biết: AH = AB = 12; D = 60°.
Tính các cạnh còn lại của hình thang ABCD. |
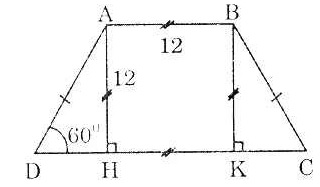 |
Giải:
* Tính AD, BC:
 AHD vuông tại H có: AH = 12 (gt);
AHD vuông tại H có: AH = 12 (gt);  = 60° (gt)
⇒ sin
= 60° (gt)
⇒ sin 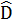 = sin60o =
= sin60o = 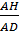 ⇒ AD =
⇒ AD = 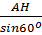 =
= 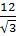 =
= 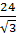 = 8
= 8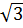 Do ABCD là hình thang cân: ⇒ AD = BC = 8
Do ABCD là hình thang cân: ⇒ AD = BC = 8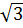 * Tính DC:
Kẻ BK ⊥ CD, giác ABKH là một hình vuông.
⇒ AB = HK = 12 (1)
Ta có:
* Tính DC:
Kẻ BK ⊥ CD, giác ABKH là một hình vuông.
⇒ AB = HK = 12 (1)
Ta có:  AHD =
AHD =  BKC ⇒ HD = KC
mà HD =
BKC ⇒ HD = KC
mà HD =  AD = 4
AD = 4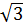 (
( AHD là nửa tam giác đều)
⇒ HD = KC = 4
AHD là nửa tam giác đều)
⇒ HD = KC = 4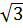 (2)
Từ (1) và (2), suy ra:
DC = DH + HK + KC = 4
(2)
Từ (1) và (2), suy ra:
DC = DH + HK + KC = 4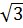 + 12 + 4
+ 12 + 4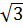 = 8
= 8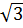 + 12
Vậy các cạnh còn lại của ABCD là:
AD = BC = 8
+ 12
Vậy các cạnh còn lại của ABCD là:
AD = BC = 8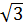 ; CD = 12 + 8
; CD = 12 + 8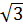
© Bản quyền thuộc về
Bài kiểm tra. Ghi rõ nguồn Bài kiểm tra.com khi sao chép nội dung này.