© 2020 Bài Kiểm Tra.com. All Rights Reserved.
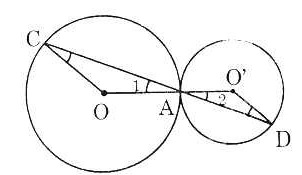
| Tam giác COA cân: Tam giác DO’A cân: Mà ⇒ |
 |
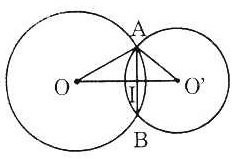
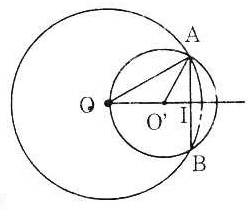
| a) Trường hợp O và O’ nằm khác phía đối với AB. Ta có: AI = OI2 = OA2 – AI2 = 400 - 144 = 256 ⇒ OI = 16 OI2 = O’A2 – AI2 = 225 - 144 = 81 ⇒ OI’ =9 Ta có: OO’ = OI + OI’ = 16 + 9 = 25 (cm). b) Trường hợp O và O’ nằm cùng phía đối với AB. Ta có: OI2 = OA2 – AI2 = 256 ⇒ OI = 16 Tương tự: O’I = 9 Do đó: OO’ = OI – O’I = 16 - 9 = 7 (cm) |
  |
| Vị trí tương đối của hai đường tròn | Số điểm chung | Hệ thức giũa d, R, r |
| (O; R) dựng ( O’; r) | ||
| D > R + r | ||
| Tiếp xúc ngoài | ||
| D = R - r | ||
| 2 |
| Vị trí tương đối của hai đường tròn | Số điểm chung | Hệ thức giũa d, R, r |
| 0 | D < R - r | |
| (O; R) ở ngoài nhau ( O’; r) | 0 | |
| 1 | D = R + r | |
| Tiếp xúc trong | 1 | |
| Hai đường tròn cắt nhau | R - r < d < R + r |
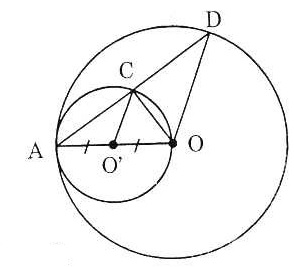
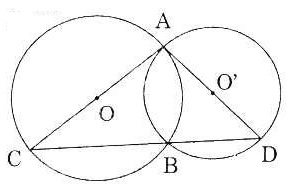
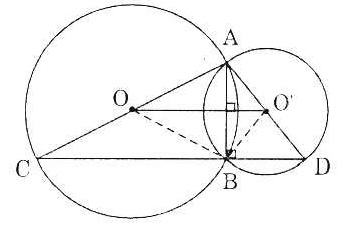
| Ta có: OO’ = OA – OA’ (hay d = R - r) Vậy (O’) tiếp xúc trong với (O) b) Tam giác AO’C cân tại O’ (do O’A = O’C) Suy ra Tương tự, tam giác AOD cân tại O. Suy ra: Từ (1) và (2) suy ra Hơn nữa: Suy ra O’C // OD Xét tam giác AOD, ta có: O’C // OD O’A = O’O Vậy O’C là đường trung bình của Suy ra: CA = CD (đpcm). |
 |
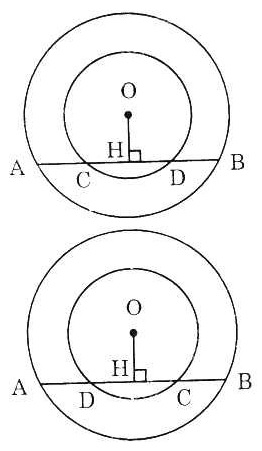
| a) Trường hợp điểm C nằm giữa A và B. Kẻ OH ⊥ OD, ta có: HA = HB và HC = HD Trừ vế theo vế, ta có: HA - HC = HB - HD Suy ra AC = BD (đpcm). b) Trường hợp điểm D nằm giữa A và B. Kẻ OH ⊥ CD, ta có: HA = HB và HC = HD Cộng vế theo vế, ta có: HA + HC = BH + HD Hay AC = BD (đpcm). |
 |
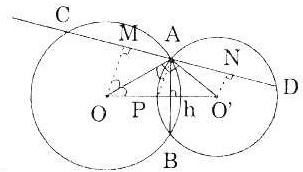
| a) Tam giác OAO’ vuông tại A: OO’2 – OA2 + O’A2 = 62 + 4,52 = 36 + 20,25 = 56,25 ⇒ OO’ = 2,5 (cm) ⇒ OO’ cắt AB tại H. Ta có: OO’ ⊥ AB tại H và HA = Trong tam giác vuông OAO’ ta lại có: AO.AO’ = AH.OO’ ⇒ AH = ' Do đó: AB = 2AH = 7,2 b) Kẻ OM ⊥ AC, O’N ⊥ AD, ta có: MA = MC = A là trung điểm của MN: ⇒ MA =NA ⇒ AC = AD Mà Tam giác APO cân ở p, ta có: Do đó: MA = AH ⇒ AC = AB. Vậy AC = AD = AB |
  |
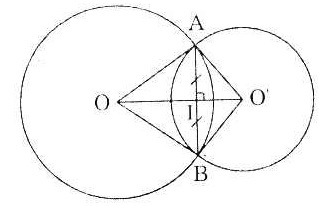
| Bài 2. Trên hình vẽ bên, hai đường tròn (O) và (O’) cắt nhau tại A và B. Cho OA = 20cm; O’A = 15cm; AB = 24. Tính đoạn nối tâm OO’. |
 |
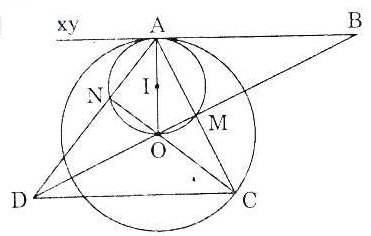
| Bài 3. Cho đường tròn (O) và một điểm A ở trên đường tròn đó. Vẽ đường tròn (I) đi qua O và tiếp xúc trong với đường tròn (O) tại A. Qua A vẽ tiếp tuyến chung xy với hai đường tròn. Dây AC của đường tròn (O) cắt đường tròn (I) tại M. Tia CO cắt đường tròn tâm I tại N. Đường thẳng OM cắt xy và tia AN lần lượt tại B và D. Chứng minh rằng: a) MA = MC b) Tứ giác ABCD là hình thoi. |
 |
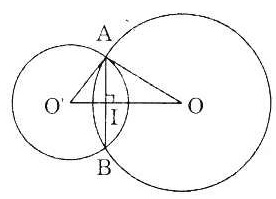
| Bài 4. Hai đường tròn (O) và (O’) cắt nhau tại A và B. Trong đó OA là tiếp tuyến của đường tròn (O’). Tính dây cung AB biết OA = 20cm, O’A = 15cm. |
 |
| Cách 1: Do các tam giác OAB và OBC cân, ta suy ra: Mặt khác, theo định lí về tổng các góc trong của một tam giác ta có: Vậy: Điểm O nằm giữa hai điểm A và C nên tia BO và nằm giữa hai tia BA và BC, do đó: Chứng minh tương tự đối với tam giác BDA ta được: Từ đó suy ra C, B, D thẳng hàng và AB ⊥ CD. Cách 2: Đường nối tâm là trục đối xứng của hình tạo bởi hai đường tròn, sử dụng định lí đường trung bình của tam giác. |
 |
Ý kiến bạn đọc
Những tin cũ hơn