Giải bài tập Toán 9, chương I: bài 6: Biến đổi đơn giản biểu thức chứa căn thức bậc hai.
2019-07-30T04:36:14-04:00
2019-07-30T04:36:14-04:00
Giải bài tập Toán 9, chương I: bài 6: Biến đổi đơn giản biểu thức chứa căn thức bậc hai.
/themes/cafe/images/no_image.gif
Bài Kiểm Tra
https://baikiemtra.com/uploads/bai-kiem-tra-logo.png
Thứ hai - 22/07/2019 06:36
Giải bài tập Toán 9, chương I: bài 6: Biến đổi đơn giản biểu thức chứa căn thức bậc hai.
Bài 1. Viết các số hoặc biểu thức dưới dấu căn thành dạng tích thích hợp rồi đưa thừa số ra ngoài dấu căn.
a) 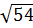 ; b)
; b) 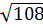 ; c) 0,1
; c) 0,1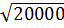 ;
d) - 0,05
;
d) - 0,05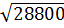 e)
e) 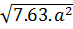 Giải:
Giải:
a) 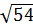 =
= 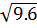 = 3.
= 3.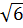 b)
b) 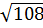 =
= 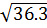 = 6
= 6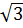 c) 0,1
c) 0,1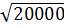 = 0,1
= 0,1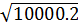 = 0,1.100.
= 0,1.100. 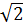 = 10
= 10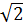 d) - 0,05
d) - 0,05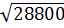 = -0,05
= -0,05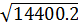 = 0,05.120
= 0,05.120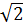 = - 6
= - 6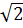 e)
e) 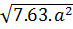 =
= 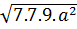 =7.3 | a | = 21|a|
Bài 2. Đưa thừa số vào trong dấu căn:
3
=7.3 | a | = 21|a|
Bài 2. Đưa thừa số vào trong dấu căn:
3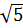 ; - 5
; - 5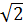 ; -
; - 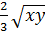 ; x
; x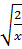 với x > 0 và y
với x > 0 và y 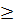 0
Giải:
* 3
0
Giải:
* 3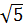 =
= 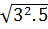 =
= 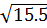 =
= 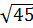 * - 5
* - 5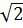 = -
= - 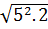 = -
= - 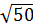 * -
* - 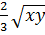 = -
= -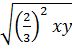 = -
= -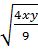 * x
* x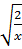 =
= 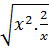 =
= 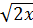 (x > 0)
Bài 3. So sánh:
a) 3
(x > 0)
Bài 3. So sánh:
a) 3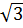 và
và 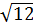 b) 7 và 3
b) 7 và 3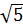 c)
c) 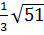 và
và 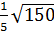 d)
d) 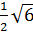 và 6
và 6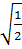 Giải:
a) Ta có: 3
Giải:
a) Ta có: 3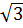 =
= 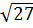 . Vì 27 > 12 ⇒
. Vì 27 > 12 ⇒ 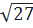 >
> 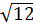 Vậy: 3
Vậy: 3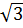 >
> 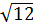 b) 3
b) 3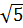 =
= 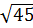 ; 7 =
; 7 = 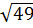 vì 49 > 45 nên 7 > 3
vì 49 > 45 nên 7 > 3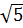 c) Ta có:
c) Ta có: 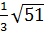 =
= 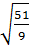 =
= 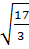 ;
; 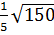 =
= 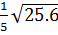 =
= 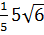 =
= 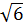 Vì:
Vì: 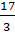 < 6 ⇒
< 6 ⇒ 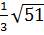 <
< 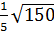 d)
d) 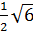 =
= 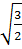 ; 6
; 6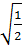 =
= 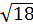 . Ta có:
. Ta có:  < 18
Vậy:
< 18
Vậy: 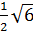 < 6
< 6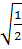 Bài 4. Giải phương trình:
a) 2
Bài 4. Giải phương trình:
a) 2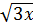 - 4
- 4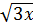 = 27 - 3
= 27 - 3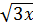 b) 3
b) 3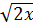 - 3
- 3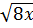 + 3
+ 3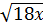 = 28
Giải:
a) 2
= 28
Giải:
a) 2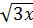 - 4
- 4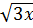 = 27 - 3
= 27 - 3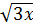 ⇔
⇔ 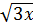 = 27 ⇔ x =
= 27 ⇔ x = 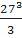 ⇔ x = 243
b) 3
⇔ x = 243
b) 3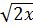 - 3
- 3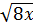 + 3
+ 3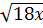 = 28
⇔ 3
= 28
⇔ 3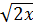 - 3
- 3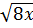 + 3
+ 3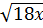 = 28
⇔ 14
= 28
⇔ 14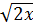 = 28 ⇔
= 28 ⇔  = 2 ⇔ 2x = 4 ⇔ x =2
Bài 5. Rút gọn:
a)
= 2 ⇔ 2x = 4 ⇔ x =2
Bài 5. Rút gọn:
a) 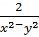
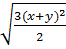 với x > 0, y > 0 và x khác y
b)
với x > 0, y > 0 và x khác y
b) 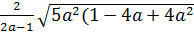 ) với a > 0,5
Giải:
a)
) với a > 0,5
Giải:
a) 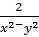
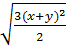 =
= 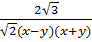 .|x + y| =
.|x + y| = 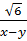 b)
b) 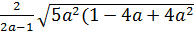 ) =
) = 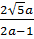 | 1 - 2a| = 2
| 1 - 2a| = 2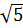 a
* Khử mẫu biểu thức để lấy căn (bài 6 và bài 7)
Bài 6.
a
* Khử mẫu biểu thức để lấy căn (bài 6 và bài 7)
Bài 6. 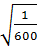 ;
; 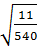 ;
; 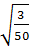 ;
; 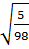 ;
; 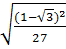 Giải:
Giải:
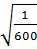 =
= 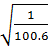 =
= 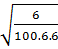 =
= 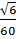
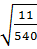 =
= 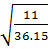 =
= 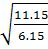 =
= 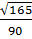
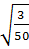 =
= 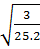 =
= 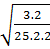 =
= 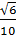
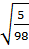 =
= 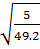 =
= 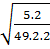 =
= 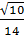
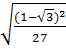 =
= 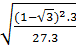 =
= 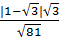 =
= 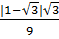 =
= 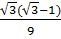 Vì 1 <
Vì 1 < 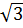 ⇒ 1 -
⇒ 1 - 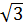 < 0 ⇒ 1 -
< 0 ⇒ 1 - 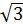 =
= 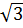 – 1
Vậy:
– 1
Vậy: 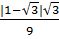 =
= 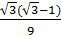 Bài 7. ab
Bài 7. ab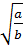 ;
; 
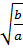 ;
; 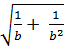 ;
; 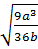 ; 3xy
; 3xy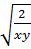 Giải:
a) Xét ab
Giải:
a) Xét ab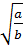 , do
, do 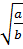 có nghĩa nên a, b cùng dấu
ab
có nghĩa nên a, b cùng dấu
ab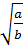 = ab
= ab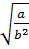 =
= 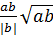 + b > 0 ⇒
+ b > 0 ⇒ 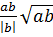 = a
= a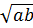 + b < 0 ⇒
+ b < 0 ⇒ 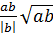 = -
= - 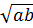 b)
b) 
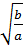 =
=  .
.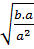 =
= 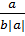 =
= 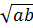 + a > 0 ⇒
+ a > 0 ⇒ 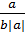
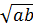 =
= 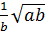 =
= 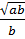 . Vậy
. Vậy 
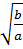 =
= 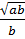 + a < 0 ⇒
+ a < 0 ⇒ 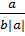
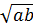 = -
= - 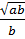 . Vậy
. Vậy 
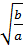 = -
= - 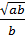 c)
c) 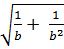 =
= 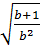 =
= 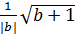 + b > 0 ⇒
+ b > 0 ⇒ 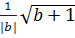 =
= 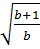 . Vậy:
. Vậy: 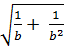 =
= 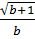 + b < 0 ⇒
+ b < 0 ⇒ 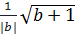 = -
= - 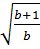 . Vậy:
. Vậy: 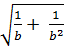 = -
= - 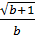 d)
d) 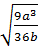 =
= 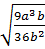 =
= 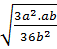 =
= 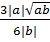 =
= 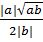 Do
Do 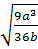 có nghĩa nên a và b cùng dấu
Do đó:
có nghĩa nên a và b cùng dấu
Do đó: 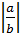 =
=  , vậy:
, vậy: 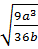 =
= 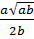 e) 3xy
e) 3xy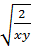 = 3
= 3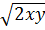 Trục căn thức ở mẫu với giả thiết các biểu thức chữ đều có nghĩa (từ bài 8 đến bài 10)
Bài 8.
Trục căn thức ở mẫu với giả thiết các biểu thức chữ đều có nghĩa (từ bài 8 đến bài 10)
Bài 8. 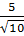 ;
; 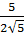 ;
; 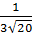 ;
; 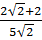 ;
; 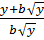 Giải:
Giải:
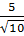 =
= 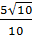 =
= 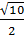
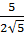 =
= 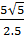 =
= 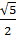
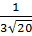 =
= 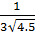 =
= 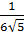 =
= 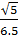 =
= 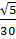
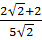 =
= 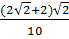 =
= 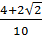 =
= 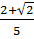
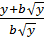 =
= 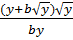 =
= 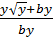 =
= 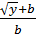 Bài 9.
Bài 9. 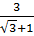 ;
; 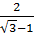 ;
; 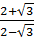 ;
; 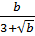 ;
; 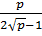 Giải:
Giải:
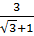 =
= 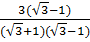 =
= 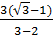 =
=  (
(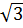 -1)
-1)
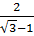 =
= 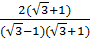 =
= 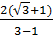 =
= 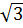 +1
+1
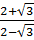 =
= 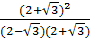 =
= 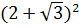
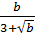 =
= 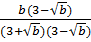 =
= 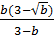
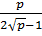 =
= 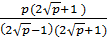 =
= 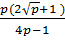 Bài 10.
Bài 10. 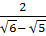 ;
; 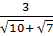 ;
; 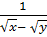 ;
; 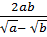 Giải:
Giải:
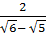 =
= 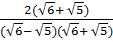 = 2(
= 2(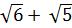 )
)
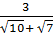 =
= 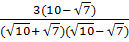 =
= 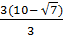 =
= 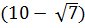
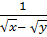 =
= 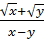
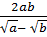 =
= 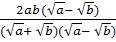 =
= 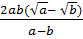 BÀI TẬP LÀM THÊM
Bài 1: Trục căn thức ở mẫu số:
a)
BÀI TẬP LÀM THÊM
Bài 1: Trục căn thức ở mẫu số:
a) 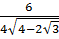 b)
b) 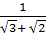 ;
; 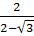 ;
; 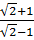 ;
; 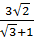 c)
c) 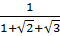 ;
; 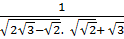 Giải:
a) Ta có:
Giải:
a) Ta có: 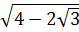 =
= 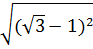 = |
= |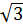 -1| =
-1| = 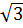 -1
Do đó:
-1
Do đó: 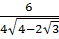 =
= 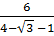 =
= 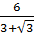 =
= 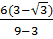 = 3 -
= 3 - 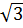 b) Ta có:
b) Ta có: 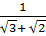 =
= 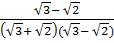 =
= 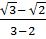 =
= 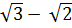 Ta có:
Ta có: 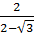 =
= 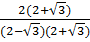 =
= 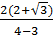 = 4 +
= 4 + 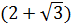 Ta có:
Ta có: 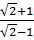 =
= 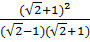 =
= 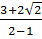 = 3 +
= 3 + 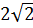 Ta có:
Ta có: 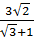 =
= 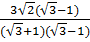 =
= 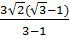 =
= 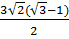 c) Ta có:
c) Ta có:  =
= 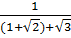 =
= 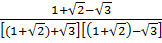 =
= 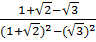 =
= 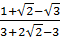 =
= 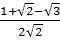 =
= 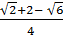 Vậy:
Vậy: 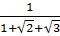 =
= 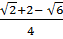 Ta có:
Ta có: 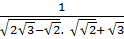 =
= 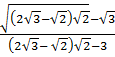 =
= 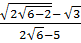 =
= 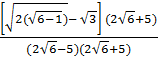 =
= 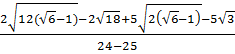 = 6
= 6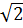 + 5
+ 5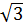 -
- 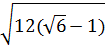 – 5
– 5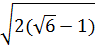 Bài 2. Tính giá trị của biểu thức:
A=
Bài 2. Tính giá trị của biểu thức:
A= 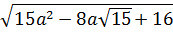 với a =
với a = 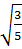 +
+ 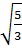 Giải:
Trước hết, ta biến đổi biểu thức dưới dấu căn:
Giải:
Trước hết, ta biến đổi biểu thức dưới dấu căn:
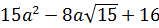 = (a
= (a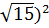 – 2.4.a
– 2.4.a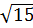 + 42 = (a
+ 42 = (a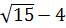 )2
Như vậy: A =
)2
Như vậy: A = 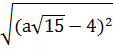 = |(a
= |(a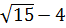 )|
Tiếp theo, ta biến đổi a:
A =
)|
Tiếp theo, ta biến đổi a:
A = 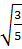 +
+ 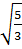 =
= 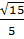 +
+ 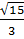 =
= 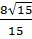 Với a =
Với a = 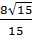 ⇒ a
⇒ a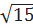 – 4 > 0
Vậy: a
– 4 > 0
Vậy: a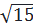 – 4 = 8 – 4 = 4
Bài 3. Tính tổng:
A =
– 4 = 8 – 4 = 4
Bài 3. Tính tổng:
A = 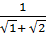 +
+ 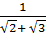 + …. +
+ …. + 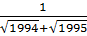 Ta có: A =
Ta có: A = 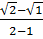 +
+ 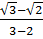 + ….+
+ ….+ 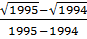 = (
= (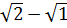 ) + (
) + (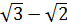 ) + (
) + (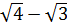 ) + …+ (
) + …+ (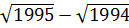 )
= (
)
= (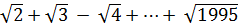 ) – (
) – (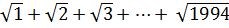 )
=
)
= 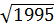 - 1
Bài 4. Tính:
a) 3
- 1
Bài 4. Tính:
a) 3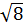 ; -2
; -2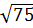 ;
; 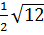 ;
; 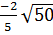 ;
; 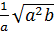 (a
(a 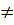 0 ; b
0 ; b 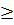 0)
b)
0)
b) 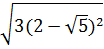 ;
; 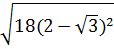 ;
; 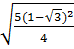 c)
c) 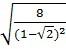 ;
; 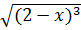 ;
; 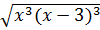 , với x > 3
d)
, với x > 3
d) 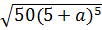 ;
; 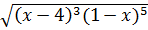 , với 1 < x < 4
Giải:
a) Ta có:
* 3
, với 1 < x < 4
Giải:
a) Ta có:
* 3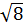 = 3.
= 3.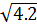 = 3
= 3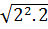 = 6
= 6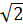 * -2
* -2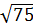 = -2
= -2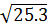 = -2
= -2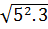 = -10
= -10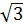 *
* 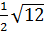 =
= 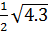 =
= 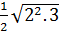 =
= 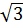 *
* 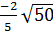 = -
= - 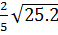 = -
= - 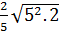 = -2
= -2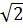 *
* 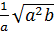 =
=  |a|
|a|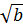 =
= 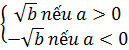 b) Ta có :
*
b) Ta có :
* 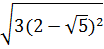 = |2 -
= |2 - 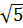 |
| 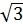 = (
= (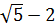 )
)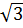 vì 2 -
vì 2 - 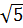 < 0
*
< 0
* 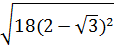 = |2-
= |2-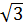 |3
|3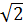 = 3(2-
= 3(2-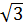 )
)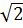 vì 2-
vì 2-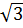 > 0
*
> 0
* 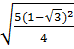 =
= 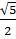 |1-
|1-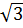 | =
| = 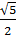 |
|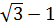 | vì 1-
| vì 1-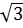 < 0
c) Ta có:
*
< 0
c) Ta có:
* 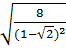 =
= 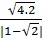 =
= 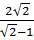 =
= 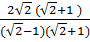 =
= 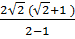 =
= 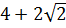 *
* 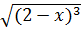 =
= 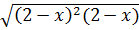 = | 2-x |
= | 2-x |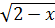 = (2 - x)
= (2 - x) 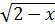 vì x
vì x 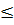 2
*
2
* 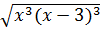 = |x(x – 3)|
= |x(x – 3)|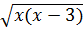 =
= 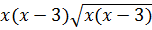 vì x > 3
d) Ta có:
*
vì x > 3
d) Ta có:
* 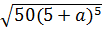 =
= 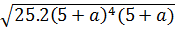 = 5(5 + a)2
= 5(5 + a)2 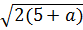 , với a
, với a 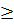 - 5
* Với 1 < x < 4
⇒ 1 – x < 0 ; x – 4 < 0 ⇒ (x - 4) (1 - x) > 0
Ta có:
- 5
* Với 1 < x < 4
⇒ 1 – x < 0 ; x – 4 < 0 ⇒ (x - 4) (1 - x) > 0
Ta có: 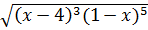 = |x - 4|(1- x)2
= |x - 4|(1- x)2 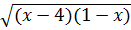 = (4 – x )(1 - x)2
= (4 – x )(1 - x)2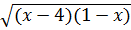 Bài 5. Giải phương trình:
Bài 5. Giải phương trình:
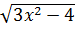 = 2x - 3
Giải:
Điều kiện: 3x2 - 4x
= 2x - 3
Giải:
Điều kiện: 3x2 - 4x 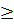 0
⇔ x (3x - 4)
0
⇔ x (3x - 4) 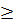 0 ⇔ x
0 ⇔ x 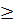
 hoặc x
hoặc x 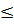 0
Với điều kiện trên phương trình được biến đổi thành:
3x2 - 4x = (2x – 3)2 ⇔ x2 – 8x + 9 = 0
⇔ (x - 4)2 – 7 = 0
⇔ (x – 4 +
0
Với điều kiện trên phương trình được biến đổi thành:
3x2 - 4x = (2x – 3)2 ⇔ x2 – 8x + 9 = 0
⇔ (x - 4)2 – 7 = 0
⇔ (x – 4 + 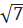 )(x – 4 -
)(x – 4 - 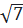 )
⇔
)
⇔ 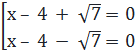 ⇔
⇔ 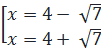 Cả hai giá trị của x đều thỏa mãn điều kiện xác định của phương trình. Vậy phương trình đã cho có hai nghiệm:
Cả hai giá trị của x đều thỏa mãn điều kiện xác định của phương trình. Vậy phương trình đã cho có hai nghiệm: 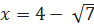 ;
; 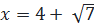 Bài 6. Giải phương trình:
a) x
Bài 6. Giải phương trình:
a) x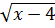 +
+ 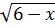 - = 10x + 27
b)
- = 10x + 27
b) 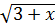 +
+ 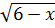 -
- 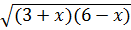 = 3
Giải:
a) Điều kiện: 4
= 3
Giải:
a) Điều kiện: 4 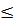 x
x 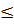 6
Ta thấy x2 - 10x + 27 = (x - 5)2 + 2
6
Ta thấy x2 - 10x + 27 = (x - 5)2 + 2 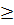 2
2
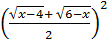
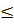
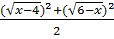 = 1
Hay:
= 1
Hay: 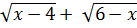
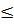 2
Vì vậy phương trình có nghiệm cần phải có:
2
Vì vậy phương trình có nghiệm cần phải có:
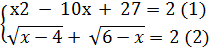 Giải phương trình (1), ta được x = 5. Giá trị thỏa mãn (2).
Vậy phương trình có nghiệm x = 5.
b) Đặt X =
Giải phương trình (1), ta được x = 5. Giá trị thỏa mãn (2).
Vậy phương trình có nghiệm x = 5.
b) Đặt X = 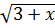 +
+ 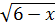 thì:
thì:
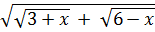 =
= 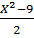 Phương trình đã đưa về dạng:
X =
Phương trình đã đưa về dạng:
X = 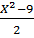 =3
⇔ 2X – X2 + 9 = 6 ⇔ X2 – 2X – 3 = 0 ⇔
=3
⇔ 2X – X2 + 9 = 6 ⇔ X2 – 2X – 3 = 0 ⇔ 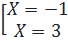 Với X = - 1 ⇔
Với X = - 1 ⇔ 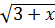 +
+ 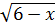 = 1, phương trình vô nghiệm.
Với X = 3 ⇔
= 1, phương trình vô nghiệm.
Với X = 3 ⇔ 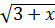 +
+ 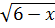 = 3
⇔
= 3
⇔ 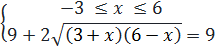 ⇔
⇔ 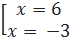
© Bản quyền thuộc về
Bài kiểm tra. Ghi rõ nguồn Bài kiểm tra.com khi sao chép nội dung này.
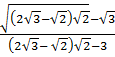
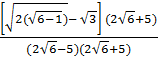
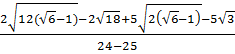
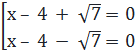 ⇔
⇔ 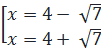
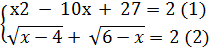
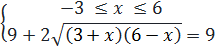 ⇔
⇔