Giải bài tập Hình học 9: Ôn tập chương III.
2019-08-31T06:45:45-04:00
2019-08-31T06:45:45-04:00
Giải bài tập Hình học 9: Ôn tập chương III: Tóm tắt kiến thức, ví dụ, hướng dẫn giải bài tập trong sách giáo khoa và bài tập luyện thêm.
/themes/cafe/images/no_image.gif
Bài Kiểm Tra
https://baikiemtra.com/uploads/bai-kiem-tra-logo.png
Thứ bảy - 31/08/2019 06:43
Giải bài tập Hình học 9: Ôn tập chương III: Tóm tắt kiến thức, ví dụ, hướng dẫn giải bài tập trong sách giáo khoa và bài tập luyện thêm.
A. Tóm tắt kiến thức (trang 101,102,103 sách giáo khoa)
B. Ví dụ
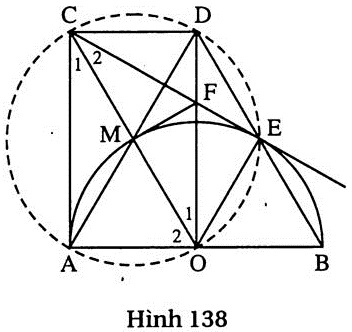
Cho nửa đường tròn (O ; R) đường kính AB và tia tiếp tuyến Ax. Trên tia Ax lấy điểm C sao cho AC = R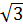 . Vẽ tiếp tuyến CE với nửa đường tròn (E là tiếp điểm). Vẽ hình chữ nhật OACD.
a) Chứng minh rằng ba điểm B, E, D thẳng hàng.
b) Gọi M là giao điểm của AD và OC. Chứng minh rằng M nằm trên nửa đường tròn (O ; R).
c) Gọi F là giao điểm của OD và CE. Chứng minh rằng MF là tiếp tuyến của đường tròn (O).
d) Tính độ dài của cung AME.
e) Chứng minh năm điểm A, C, D, E, O cùng nằm trên một đường tròn. Tính diện tích của hình tròn đó.
. Vẽ tiếp tuyến CE với nửa đường tròn (E là tiếp điểm). Vẽ hình chữ nhật OACD.
a) Chứng minh rằng ba điểm B, E, D thẳng hàng.
b) Gọi M là giao điểm của AD và OC. Chứng minh rằng M nằm trên nửa đường tròn (O ; R).
c) Gọi F là giao điểm của OD và CE. Chứng minh rằng MF là tiếp tuyến của đường tròn (O).
d) Tính độ dài của cung AME.
e) Chứng minh năm điểm A, C, D, E, O cùng nằm trên một đường tròn. Tính diện tích của hình tròn đó.
Giải (h. 138)
a) Vì CA, CE là hai tiếp tuyến nên
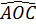 = = 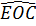 = = 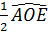
Góc B là góc nội tiếp nên B = 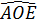 . .
Do đó 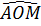 = B, suy ra BE//OC. (1) = B, suy ra BE//OC. (1)
Tứ giác OACD là hình chữ nhật nên CD // AO và CD = AO.
Do đó CD // OB và CD = OB, suy ra tứ giác OCDB là hình bình hành.
Vậy BD // OC. (2)
Từ (1) và (2) suy ra ba điểm B, E, D thẳng hàng. |
|
b) Xét tam giác AOC vuông tại A, ta có :
OC2 = OA2 + AC2 = R2 + (r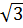 )2 = 4R2
Vậy OC = 2R.
Mặt khác OM = MC nên OM = R, suy ra M nằm trên nửa đường tròn (O ; R).
c) Ta có
)2 = 4R2
Vậy OC = 2R.
Mặt khác OM = MC nên OM = R, suy ra M nằm trên nửa đường tròn (O ; R).
c) Ta có 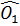 =
= 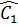 ;
; 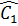 =
= 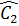 suy ra
suy ra 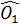 =
= 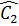 .
Vậy
.
Vậy  FOC cân.
Mặt khác OM = MC nên MF ⊥ OM.
Suy ra MF là tiếp tuyến của đường tròn (O).
b) Ta có : tg
FOC cân.
Mặt khác OM = MC nên MF ⊥ OM.
Suy ra MF là tiếp tuyến của đường tròn (O).
b) Ta có : tg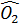 =
= 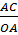 =
= 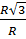 =
= 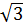 .
Suy ra
.
Suy ra 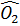 = 60o,
= 60o, 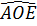 = 120o, sđ
= 120o, sđ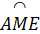 = 120o.
Độ dài của cung AME là :
l =
= 120o.
Độ dài của cung AME là :
l =  =
= 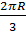 e) Tứ giác OACD là hình chữ nhật nên OAC = 90o ; ODC = 90o.
Vì CE là tiếp tuyến nên OEC = 90o.
Suy ra ba điểm A, D, E cùng nằm trên đường tròn đường kính OC. Do đó cả 5 điểm A, D, E, O, C cùng nằm trên đường tròn tâm M, bán kính MO = R.
Diện tích của đường tròn này là S =
e) Tứ giác OACD là hình chữ nhật nên OAC = 90o ; ODC = 90o.
Vì CE là tiếp tuyến nên OEC = 90o.
Suy ra ba điểm A, D, E cùng nằm trên đường tròn đường kính OC. Do đó cả 5 điểm A, D, E, O, C cùng nằm trên đường tròn tâm M, bán kính MO = R.
Diện tích của đường tròn này là S = 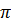 R2.
Nhận xét : Bạn có thể chứng minh năm điểm A, C, D, E, O cùng nằm trên một đường tròn bằng cách chứng minh các tứ giác OACD, OACE nội tiếp. Hai đường tròn ngoại tiếp các tứ giác này có ba điểm chung là O, A, C nên chúng trùng nhau suy ra cả năm điểm O, A, C, D, E cùng nằm trên một đường tròn.
C. Hướng dẫn giải bài tập trong sách giáo khoa
88. Trả lời: (h.139)
R2.
Nhận xét : Bạn có thể chứng minh năm điểm A, C, D, E, O cùng nằm trên một đường tròn bằng cách chứng minh các tứ giác OACD, OACE nội tiếp. Hai đường tròn ngoại tiếp các tứ giác này có ba điểm chung là O, A, C nên chúng trùng nhau suy ra cả năm điểm O, A, C, D, E cùng nằm trên một đường tròn.
C. Hướng dẫn giải bài tập trong sách giáo khoa
88. Trả lời: (h.139)
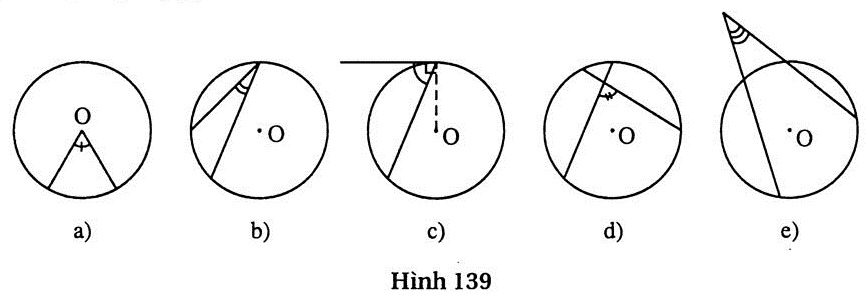 a) Góc ở tâm ;
b) Góc nội tiếp ;
c) Góc tạo bởi tia tiếp tuyến và dây cung ;
d) Góc ở đỉnh ở bên trong đường tròn ;
e) Góc có đỉnh ở bên ngoài đường tròn.
a) Góc ở tâm ;
b) Góc nội tiếp ;
c) Góc tạo bởi tia tiếp tuyến và dây cung ;
d) Góc ở đỉnh ở bên trong đường tròn ;
e) Góc có đỉnh ở bên ngoài đường tròn.
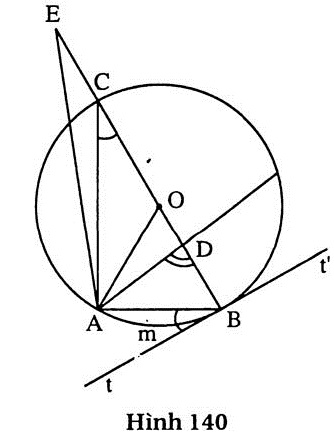
89. Giải (h. 140)
a) 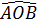 = sđ = sđ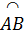 = 60o = 60o
b) 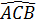 = = 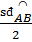 = 30o = 30o
c) 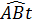 = = 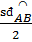 = 30o = 30o
hoặc '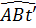 = =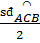 = = 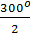 = 150 . = 150 . |
|
d) 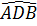 >
> 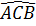 (tính chất góc ngoài của tam giác).
e)
(tính chất góc ngoài của tam giác).
e) 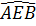 <
< 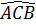 (tính chất góc ngoài của tam giác).
90. Hướng dẫn :
R =
(tính chất góc ngoài của tam giác).
90. Hướng dẫn :
R = 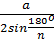 =
= 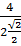 = 2
= 2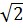 (cm)
r =
(cm)
r = 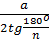 =
= 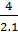 = 2 (cm)
91. Đáp số : a) 285o ; b)
= 2 (cm)
91. Đáp số : a) 285o ; b) 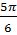 cm và
cm và 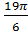 cm ; c)
cm ; c) 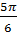 cm2 .
92. Hướng dẫn
Hình 141: S =
cm2 .
92. Hướng dẫn
Hình 141: S = 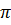 (R2 – r2) =
(R2 – r2) = 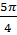 (cm2)
(cm2)
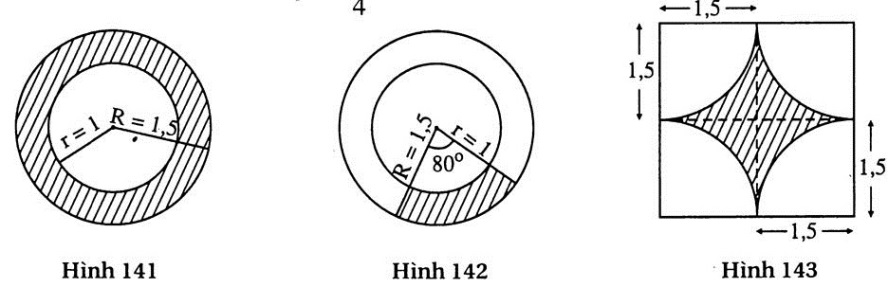 Hình 142: S =
Hình 142: S = 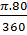
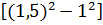 =
= 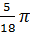 (cm2)
Hình 143: Lấy diện tích hình vuông trừ đi diện tích hình tròn bán kính 1,5cm.
(cm2)
Hình 143: Lấy diện tích hình vuông trừ đi diện tích hình tròn bán kính 1,5cm.
Đáp số: 1,94cm2.
93. Hướng dẫn :
Số vòng quay của mỗi bánh xe tỉ lệ nghịch với số răng của bánh xe.
a) Đáp số: 30 vòng.
b) Đáp số: 120 vòng.
c) Bán kính của mỗi bánh xe tỉ lệ thuận với số răng của mỗi bánh xe.
Bán kính của bánh xe A là 3cm.
Bán kính của bánh xe B là 2cm.
94. Giải:
a) Tỉ lệ học sinh ngoại trú so với học sinh toàn trường là 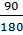 =
=  .
Vậy câu a) trả lời đúng.
b) Tỉ lệ học sinh bán trú so với học sinh toàn trường là
.
Vậy câu a) trả lời đúng.
b) Tỉ lệ học sinh bán trú so với học sinh toàn trường là 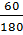 =
=  .
Vậy câu b) trả lời đúng.
c) Tỉ lệ phần trăm học sinh nội trú là :
.
Vậy câu b) trả lời đúng.
c) Tỉ lệ phần trăm học sinh nội trú là :
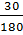 .100%
.100% 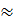 16,67%
d) Số học sinh ngoại trú là :
1800 x
16,67%
d) Số học sinh ngoại trú là :
1800 x  = 900 (học sinh).
Số học sinh bán trú là :
1800 x
= 900 (học sinh).
Số học sinh bán trú là :
1800 x  = 600 (học sinh).
Số học sinh nội trú là :
1800 - (900 + 600) = 300 (học sinh).
= 600 (học sinh).
Số học sinh nội trú là :
1800 - (900 + 600) = 300 (học sinh).
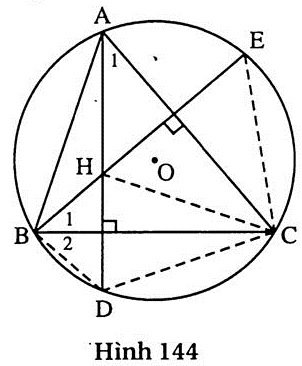
95. Giải (h.144)
a) Ta có 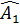 = =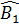 (cùng phụ với góc ACB). (cùng phụ với góc ACB).
Do đó 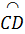 = = 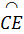 , suy ra CD = CE. , suy ra CD = CE.
b) Ta có 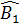 = = 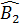 (cùng bằng (cùng bằng 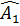 ). Tam giác BHD có BC vừa là đường phân giác, vừa là đường cao nên ABHD cân. ). Tam giác BHD có BC vừa là đường phân giác, vừa là đường cao nên ABHD cân.
c) Đường thẳng BC là đường trung trực của HD, do đó CD = CH.
|
|
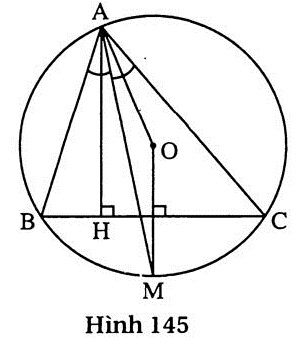
96. Giải (h. 145)
a) Ta có 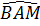 = = 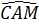 , suy ra , suy ra 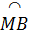 = = 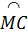 , do đó OM ⊥ BC và OM đi qua trung điểm của BC. , do đó OM ⊥ BC và OM đi qua trung điểm của BC.
b) Ta có AH // OM (cùng vuông góc với BC).
Suy ra 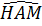 = = 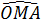 (so le trong). (so le trong).
Ta có 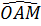 = = 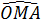 (vì (vì  OAM cân). OAM cân).
Do đó 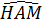 = = 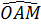 . Vậy tia AM là tia phân giác của góc . Vậy tia AM là tia phân giác của góc 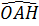 |
|
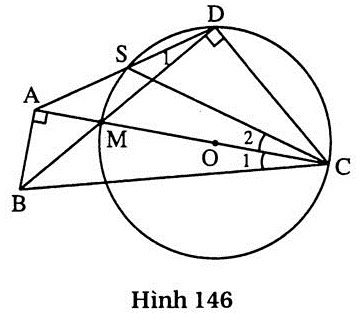
97. Giải (h. 146)
a) Ta có 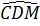 – 90o (góc nội tiếp chắn nửa đường tròn). – 90o (góc nội tiếp chắn nửa đường tròn).
Mặt khác 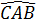 = 90o (giả thiết). = 90o (giả thiết).
Vậy tứ giác ABCD nội tiếp đường tròn đường kính BC.
|
|
b) Ta có 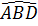 =
= 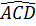 (hai góc nội tiếp cùng chắn cung AD).
c) Xét đường tròn đường kính BC, ta có
(hai góc nội tiếp cùng chắn cung AD).
c) Xét đường tròn đường kính BC, ta có 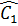 =
= 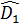 (hai góc nội tiếp cùng chắn cung AB).
Ta còn có
(hai góc nội tiếp cùng chắn cung AB).
Ta còn có 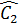 =
= 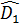 (hai góc nội tiếp cùng chắn cung SM của đường tròn (O)).
Suy ra
(hai góc nội tiếp cùng chắn cung SM của đường tròn (O)).
Suy ra 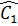 =
= 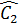 , do đó tia CA là tia phân giác của góc SCB.
Nhận xét: Sau khi chứng minh được một tứ giác nội tiếp, bạn có thể tìm ra các cặp góc nội tiếp cùng chắn một cung thì bằng nhau. Đó chính là một lợi ích của tứ giác nội tiếp.
, do đó tia CA là tia phân giác của góc SCB.
Nhận xét: Sau khi chứng minh được một tứ giác nội tiếp, bạn có thể tìm ra các cặp góc nội tiếp cùng chắn một cung thì bằng nhau. Đó chính là một lợi ích của tứ giác nội tiếp.
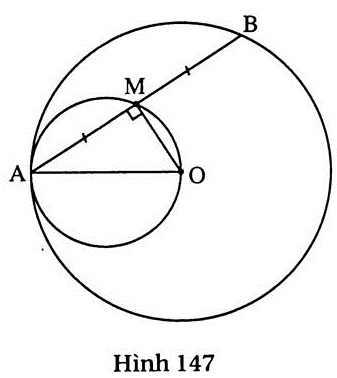
98. Giải (h. 147)
+ Phần thuận
Vì MA = MB nên OM ⊥ AB, do đó AMO = 90o
Điểm M nhìn đoạn thẳng AO cho trước dưới một góc vuông nên điểm M nằm trên đường tròn đường kính AO.
+ Phần đảo
Lấy điểm M bất kì trên đường tròn đường kính AO. Vẽ dây AB đi qua M. Ta phải chứng minh M là trung điểm của AB.
Thực vậy, ta có 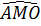 = 90o (góc nội tiếp chắn nửa đường tròn), suy ra OM ⊥ AB, do đó MA = MB = 90o (góc nội tiếp chắn nửa đường tròn), suy ra OM ⊥ AB, do đó MA = MB |
|
Kết luận: Quỹ tích các trung điểm M của các dây AB, khi B di động trên đường tròn (O) là đường tròn đường kính OA.
99. Hướng dẫn: Xem cách dựng Bài 49.
D. Bài tập luyện thêm
1. Cho đường tròn (O ; R), hai đường kính AB và CD. Đường thảng xy tiếp xúc với đường tròn tại B. Các đường thẳng AC, AD cắt đường thẳng xy lần lượt tại M và N.
a) Tứ giác ACBD là hình gì ? Chứng minh.
b) Chứng minh AC.AM = 4R2.
c) Chứng minh tứ giác MNDC nội tiếp.
d) Cho R = 3cm, BAC = 30o, tính diện tích hình viên phân giới hạn bởi dây BC và cung nhỏ BC.
2. Cho đường tròn (O ; R) và một đường thẳng d không cắt đường tròn (O). Khoảng cách từ O đến đường thẳng d nhỏ hơn R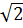 . Lấy điểm M
. Lấy điểm M 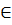 d. Vẽ các tiếp tuyến MA, MB với đường tròn (O) trong đó A, B là các tiếp điểm. Gọi H là giao điểm của AB và OM.
a) Chứng minh rằng tứ giác MAOB nội tiếp.
b) Chứng minh tích OM.OH có giá trị không đổi.
c) Khi M di động trên đường thẳng d thì tâm I của đường tròn nội tiếp
d. Vẽ các tiếp tuyến MA, MB với đường tròn (O) trong đó A, B là các tiếp điểm. Gọi H là giao điểm của AB và OM.
a) Chứng minh rằng tứ giác MAOB nội tiếp.
b) Chứng minh tích OM.OH có giá trị không đổi.
c) Khi M di động trên đường thẳng d thì tâm I của đường tròn nội tiếp  MAB di động trên đường nào ?
d) Đường thẳng qua O và vuông góc với OM cắt tia MB tại N. Xác định vị trí của M để diện tích AMON nhỏ nhất.
3. Cho đường tròn (O ; R) và dây AB cố định. Điểm M thuộc cung lớn AB, N là trung điểm của AB. Vẽ đường tròn (O’) đi qua M và tiếp xúc với AB tại A. Tia MN cắt đường tròn (O’) tại C và cắt đường tròn (O) tại D.
a) Chứng minh tứ giác ACBD là hình bình hành.
b) AB là tiếp tuyến của đường tròn ngoại tiếp
MAB di động trên đường nào ?
d) Đường thẳng qua O và vuông góc với OM cắt tia MB tại N. Xác định vị trí của M để diện tích AMON nhỏ nhất.
3. Cho đường tròn (O ; R) và dây AB cố định. Điểm M thuộc cung lớn AB, N là trung điểm của AB. Vẽ đường tròn (O’) đi qua M và tiếp xúc với AB tại A. Tia MN cắt đường tròn (O’) tại C và cắt đường tròn (O) tại D.
a) Chứng minh tứ giác ACBD là hình bình hành.
b) AB là tiếp tuyến của đường tròn ngoại tiếp  BCM.
c) Xác định vị trí của M để diện tích tứ giác ACBD lớn nhất.
Hướng dẫn - Đáp số
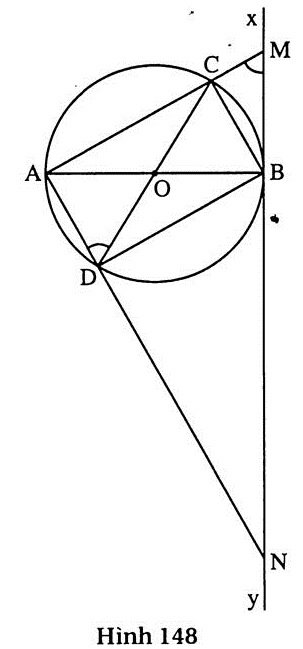
1. (h.148)
a) Tứ giác ACBD là hình chữ nhật.
b) Áp dụng hệ thức AB2 = AC. AM = 4R2 của tam giác ABM vuông tại B.
c) Ta có
BCM.
c) Xác định vị trí của M để diện tích tứ giác ACBD lớn nhất.
Hướng dẫn - Đáp số
1. (h.148)
a) Tứ giác ACBD là hình chữ nhật.
b) Áp dụng hệ thức AB2 = AC. AM = 4R2 của tam giác ABM vuông tại B.
c) Ta có 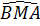 =
= 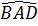 (cùng phụ với
(cùng phụ với 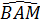 ).
Mặt khác
).
Mặt khác 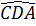 =
= 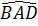 (vì
(vì  AOD cân).
Do đó
AOD cân).
Do đó 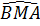 =
= 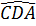 Suy ra tứ giác MNDC nội tiếp.
Suy ra tứ giác MNDC nội tiếp.
d) Ta có 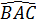 = =  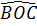 , do đó , do đó 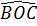 = 60o, = 60o,
Vậy  BOC đều. BOC đều.
Diện tích hình quạt OBCO là :
S1 = 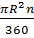 = = 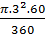 = = 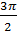 (cm2) (cm2)
Diện tích  BOC là : BOC là :
S2 = 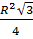 = = 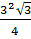 = = 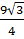 (cm2) (cm2)
Diện tích hình viên phân là :
S = S1 – S2 = 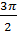 - - 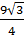  0,8 (cm2) 0,8 (cm2) |
|
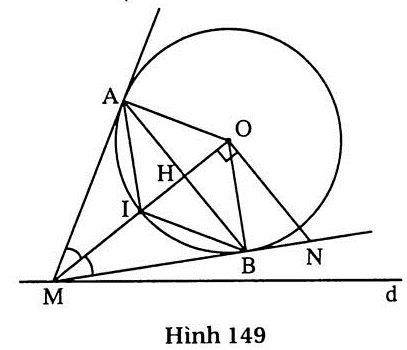
2. (h.149). a) 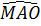 + + 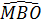 = 180o nên tứ giác MAOB nội tiếp. = 180o nên tứ giác MAOB nội tiếp.
b) Áp dụng hệ thức trong tam giác OAM vuông tại A, ta có :
OM.OH = OA2 = R2.
c) Gọi I là giao điểm của OM với đường tròn (O)
Ta có : 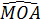 = = 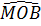 ⇒ ⇒ 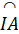 = = 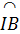
Do đó 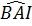 = = 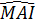 ; ; 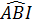 = = 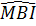 . .
Vây I là tâm của đường tròn nội tiếp  MAB và I di động trên đường tròn (O). MAB và I di động trên đường tròn (O). |
|
d) Diện tích  MON là :
S =
MON là :
S =  OB.MN=
OB.MN=  R.MN.
S nhỏ nhất ⇔ MN nhỏ nhất.
Ta có MN = MB + BN
R.MN.
S nhỏ nhất ⇔ MN nhỏ nhất.
Ta có MN = MB + BN 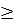 2
2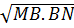 = 2R.
Vậy min MN = 2R ⇔ MB = BN = R.
⇔ OM = R
= 2R.
Vậy min MN = 2R ⇔ MB = BN = R.
⇔ OM = R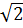 Vậy M
Vậy M 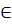 d và M cách O một khoảng R
d và M cách O một khoảng R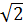
3. (h.150).
a) Ta có : 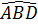 = = 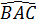 (= (=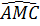 ). ).
Vậy  NBD = NBD =  NAC (g.c.g) ⇒ ND = NC, dẫn tới ACBD là hình bình hành. NAC (g.c.g) ⇒ ND = NC, dẫn tới ACBD là hình bình hành.
b) Ta có : 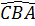 = = 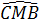 (= (= 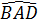 ) )
mà 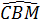 = =  sđ sđ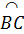 nên nên 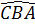 = sđ = sđ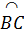 . .
Do đó AB là tiếp tuyến của đường tròn ngoại tiếp  BCM. BCM.
c) Diện tích hình bình hành ACBD gấp hai lần diện tích  ABD. ABD.
Do đó SACBD lớn nhất ⇔ SABD lớn nhất
⇔ D là điểm chính giữa của cung nhỏ AB
⇔ M là điểm chính giữa của cung lớn AB. |
|
© Bản quyền thuộc về
Bài kiểm tra. Ghi rõ nguồn Bài kiểm tra.com khi sao chép nội dung này.